双环盘式刀库结构参数优化*
卢晓红,韩鹏卓,武文毅,李光俊,贾振元
(大连理工大学 精密与特种加工教育部重点实验室,辽宁 大连 116024)
0 引言
重型加工中心和高档加工中心消费额的快速增长,决定了其关键功能部件——大型刀库及自动换刀装置的需求相应增长。大型刀库及自动换刀装置的主要作用在于减少加工过程中的非切削时间[1],是体现重型加工中心性能的重要标志,国际市场的需求量相当可观。我国大型刀库及自动换刀装置每年的需求量在3500 套左右[2]。大型刀库及自动换刀装置基本依赖进口,所以开发、研制完全拥有我国自主知识产权的大型刀库及换刀装置系列产品及关键零部件已经迫在眉睫。鉴于此,本文依托“高档数控机床与基础制造装备”科技重大专项课题“大型链式刀库和高速盘式刀库及自动换刀装置开发研究”,进行圆盘刀库刀盘结构参数优化研究,以增大储刀量。
盘式刀库呈盘状,刀具沿盘面垂直排列(包括径向取刀和轴向取刀)、沿盘面径向排列或成锐角排列的形式的刀库,结构简单、紧凑,应用较多,但刀具单环排列,空间利用率低[3],刀具数量一般不多于32 把;若增加刀库容量必须使刀库的外径增大,那么转动惯量也相应增大,选刀运动时间长。双环布刀合理的刀库结构参数可以有效解决刀库转动惯量与刀盘尺寸限制的矛盾,因此,有必要对刀库刀盘结构参数进行优化研究。目前,国内外未见双环盘式刀库结构参数优化研究的相关报道。本文在详细研究相关刀库关键技术的基础上,以YP5048G 双环盘式刀库的结构参数优化研究为应用实例,综合考虑各种约束条件,采用数学建模分析和有限元分析相结合的方法,对其进行结构参数优化,以增大储刀量,扩大工作范围,解决刀库转动惯量与刀盘尺寸限制的矛盾。
1 刀盘结构参数优化建模
对于双环盘式刀库的结构参数优化问题,以转动惯量最小为优化目标,以满足非干涉为约束条件,运用Matlab 编程求解,获得优化结构参数。
1.1 建立目标函数
刚体转动惯量的大小表现了刚体转动状态改变的难易程度[4],在刀库允许的应力及变形范围内,希望刀库的转动惯量尽量小,因此,以刀库的转动惯量最小为优化目标。
如图1 为双环盘式刀库布刀示意图。设刀盘直径为d1,刀库外环布刀直径为d2,内环布刀直径为d3,刀盘厚度为b,内环布刀个数为n1,外环布刀个数为n2。

图1 双环刀库示意图
该双环盘式刀库的转动惯量近似为刀盘本体对中心轴的转动惯量、刀库内环刀具对中心轴的转动惯量及刀库外环刀具对中心轴的转动惯量之和。
设圆盘本体的半径为R,质量为M,将圆盘分成无数同心的细圆环,任一圆环的半径为ri,宽度为dri,则圆环的质量如式(1):

圆盘对中心轴的转动惯量如式(2):

刀盘本体的转动惯量如式(3):

式中:ρ——刀盘本体的密度,材料为HT250,其密度为7.3 ×10-6kg/mm3;
a——刀盘本体中心孔直径,为常量,在此取200mm;
d1——刀盘本体的直径;
b——刀盘本体的厚度。

同理,内环刀具对刀库中心轴的转动惯量如式(5):

式中:m——刀具(包括刀具、刀套及刀柄)的平均重量,常量,为15kg;
n1——刀库外环的刀位数;
d2——刀库外环直径;
n2——刀库内环的刀位数;
d3——刀库内环的直径。
因此,所建立的目标函数模型如式(6):

1.2 确定约束条件
(1)受整机工作空间的限制,刀库外环直径需满足约束条件d1≤1280;
(2)保证刀库内外环之间不干涉需要满足的约束条件(已知刀套的直径为φ100mm),由几何关系可知:d2-d3≥160;
(3)刀套安装孔距刀盘边缘须预留满足锁刀刚性的边缘距离(刀位孔的尺寸为φ100mm,满足锁刀刚性的最小边缘距离为15mm):d1-d2≥130;
(4)保证刀库内环直径不小于刀库中心孔的直径:d3≥200;
(5)根据所选刀套(刀套安装与刀盘配合的最小尺寸为188mm)以及考虑避免应力集中现象,刀盘厚度应至少大于最小配合尺寸20mm,因此刀盘厚度须满足:b ≥208;
(6)根据设计要求,刀盘内环与外环的储刀数之和为48 把,并且为满足内环出刀,内环增设一个空刀位,故有:n1+ n2= 49 (n1,n2皆为正整数);
(7)保证外环相邻两刀位之间不干涉需要满足的约束条件(已知刀套安装与刀盘配合的最小尺寸为120mm),在图1 中的ΔOMN 中,MN ≥120mm,由几何关系可知:

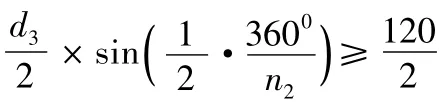
为表达方便:

故目标函数转化为式(7):

约束条件:
(1)d1≤1280 转化为:x1-1280 ≤0;
(2)d2-d3≥160 转化为:x3-x2+160 ≤0;
(3)d1-d2≥130 转化为:x2-x1+130 ≤0;
(4)d3≥200 转化为:- x3+200 ≤0;
(5)b ≥208 转化为:- x4+208 ≤0;
(6)n1+ n2= 49 转化为:x5+ x6-49 = 0;
1.3 模型求解
本文的优化问题属于多变量有约束非线性函数的最小值优化问题[5]。选用MATLAB 软件的优化工具箱中的fmincon 函数进行求解[6-8]。首先编写以下两个.m 文件:
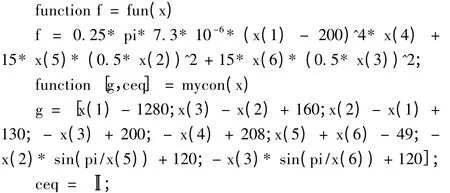
主程序如下:

运行结果如下:


2 结构参数优化刀盘静态特性仿真分析
根据优化结果,建立装满48 把刀(内环空出一个刀位进行导刀)时的三维实体模型(如图2 所示)进行应力变形分析,以验证其是否满足实际工作要求[9]。

图2 刀库模型图
刀盘本体材料为灰铸铁,模拟刀具材料为45 号钢,平均刀具重量为15kg。网格划分结果如图3 所示。在此,主要验证刀库在受自身重力下的应力及变形情况。由于刀库中的刀具不参与切削,无需对其进行加载分析。刀库受重力的变形图如图4 所示。求解之后,刀具顶端变形量最大,其值为3.97μm,远小于单环布刀圆盘刀库最大变形值35μm。刀库受自身重力时的应力图如图5 所示。刀库中心孔处所受应力值最大,其值为0.53MPa,小于单环布刀圆盘刀库极限应力值29.4MPa。故此刀库静态性能较好。

图3 双环刀库网格图

图4 加载示意图

图5 刀库轴向应力图
3 模态分析
对刀库整体结构进行模态分析,可以得到整体结构的动态特性。模态分析的前处理过程、边界条件及约束与静力分析相同,分析时采用空间迭代法提取模态[10],求解时共扩展了五阶模态,其固有频率如表1 所示,各阶模态振型如图6 所示。

表1 刀库各阶固有频率
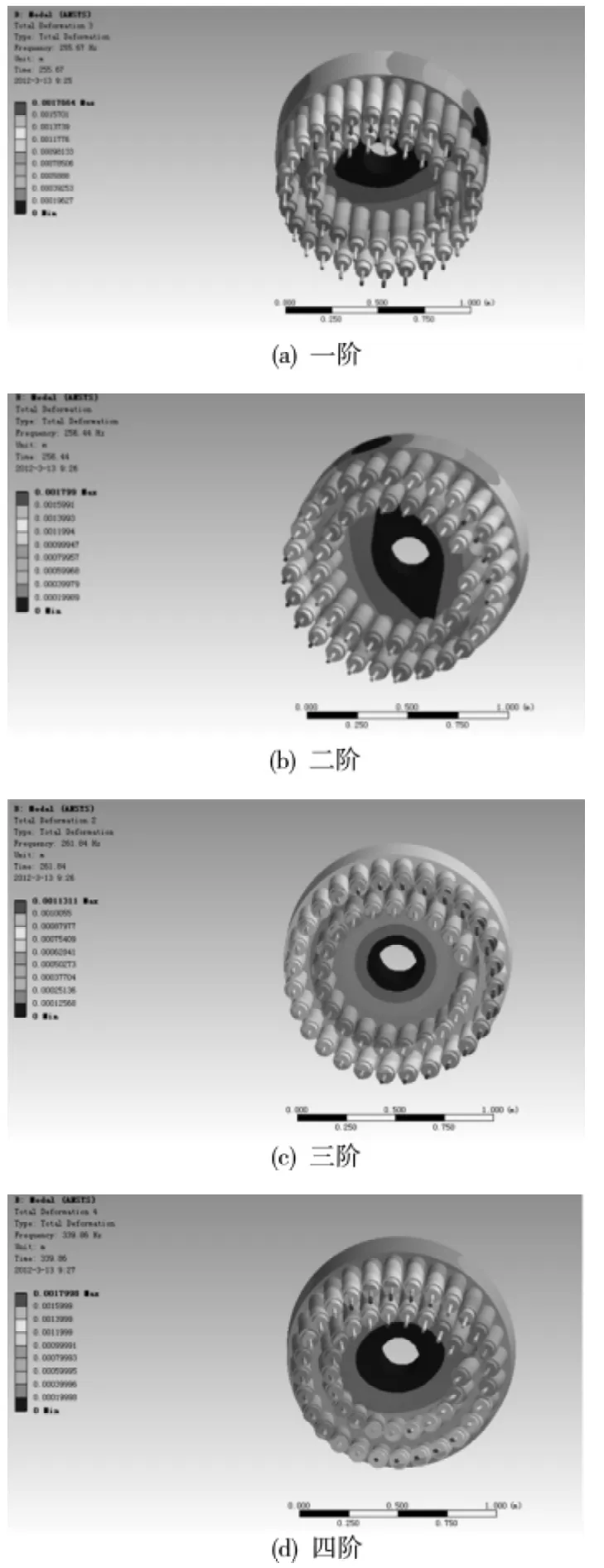

图6 刀库整体的前五阶模态振型图
由刀库整体的前五阶模态振型图可知,双环布刀盘式刀库的整体薄弱环节发生在轴向靠近边缘的地方,即刀库轴向刚度相对较弱。其中一阶及二阶振动沿轴向前后摆动;四阶和五阶时振动破坏较为严重,振动在轴向和径向都有发生。在实际应用过程中,需要避开这些共振频率以保证刀库工作的可靠性。
4 结论
针对双环盘式刀库刀盘尺寸惯性与转动惯量之间的矛盾,本文通过对双环盘式刀库刀盘结构参数优化设计问题进行抽象,建立了刀盘结构优化设计数学模型,并对优化后的刀盘进行了有限元静态特性分析及动态特性分析,仿真结果证实了结构参数优化后的刀库刀盘符合静态测试的变形要求,从而证明了所提出的结构参数优化设计方案的合理性。所提出的刀盘结构参数优化设计方案很好地解决了转动惯量与刀盘尺寸惯性的矛盾,目前已应用于大连高金数控集团有限公司的双环布刀盘式刀库新产品的研发中。
[1]付承云. 数控功能部件选用指导手册[M]. 北京:机械工业出版社,2011.
[2]中国机械工业年鉴编辑委员会,中国机床工具工业协会编. 中国机床工具工业年鉴[M]. 北京:机械工业出版社,2009.
[3]蔡厚道,吴暐. 数控机床构造[M]. 北京:北京理工大学出版社,2007.
[4]http://hi. baidu. com/jis2007/blog/item/67b53db358b42da 8d8335ae0.html.
[5]Zhi-bin ZHU;Jin-bao JIAN;Cong ZHANG. An SQP algorithm for mathematical programs with nonlinear complementarity constraints[J]. Applied Mathematics and Mechanics.2009,30(5):659-668.
[6]陈杰. MATLAB 宝典[M]. 北京:电子工业出版社,2007.
[7]邢晓林,曹延芬. MATLAB 软件在法兰优化设计中的应用[J]. 兰州石化职业技术学院学报,2007,7(3):18-20.
[8]王春香,冯慧忠. MATLAB 软件在机械优化设计中的应用[J]. 机械设计,2004,21(7):52-54.
[9]浦广益. ANSYS Workbench 12 基础教程与实例详解[M]. 北京:中国水利水电出版社,2010.
[10]傅志方,华宏星. 模态分析理论与应用[M]. 上海:上海交通大学出版社,2000.

