基于联合字典学习的图像去噪

余 雷，满家巨*，刘利刚

(1.湖南师范大学数学与计算机科学学院，中国长沙 410081;2.浙江大学数学系，中国杭州 310027)

图像去噪问题是由观测的退化图像估计原图像要求在有效去除噪声的同时能保证图像边缘等重要特征.利用稀疏表达的思想进行图像去噪当前受到研究者们的关注.该方法最初只是考虑了单一小波系数的稀疏性，并由此提出一系列收缩算法［1-2］.文献［3］利用冗余字典来保证移不变性质;文献［4-6］以具有方向性的多尺度冗余变换如curvelet，contourlet，wedgelet，bandlet 作为字典的方法.这些算法均采用预先选取一组小波基作为字典.但是利用这些已知字典表示图像缺乏自适应性.目前比较流行基于学习的字典获取方式，如文献［7］中，作者进行了两组实验:分别从大量自然图像集和噪声图像本身学习出字典，均获得较好的去噪效果.

一般利用贝叶斯方法求解图像处理中的反问题时，都会对图像做一个先验假设，例如图像的空间平滑性、最大(小)熵或者在某些变换域稀疏等.文献［8］提出利用稀疏表达进行图像上采样，文中作者通过从自然图像的高分辨率和低分辨率版本中成对采样学习字典，最终得到图像边缘和细节得到较好恢复的上采样结果.受该文献启发，本文尝试将自然图像和其经过预处理的噪声图像对作为样本联合训练构造一种新的字典，再利用图像在相应字典上的稀疏分解达到去噪声的目的.

1 基于稀疏表达的图像去噪

匹配追踪［9］和基追踪［10］去噪算法的提出将图像去噪问题转换成图像在冗余字典上的稀疏分解问题.通常图像去噪算法处理的是受均值为零的高斯白噪声污染的图像，即希望从以下观测图像y 估计图像的清晰版本:y=x+N(0，δ).文献［7］提出的稀疏表示模型假设自然图像可以被某一字典D 近似稀疏表示，即的解是稀疏的，其中‖α‖0表示向量α 中非0 元素的个数.可以通过求解下式构造最大后验概率估计以去除噪声:

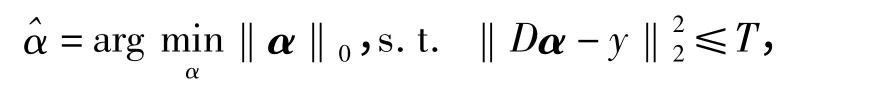
其中，T 由用字典D 稀疏表示图像的准确程度和图像噪声的标准差σ 决定.该优化的求解可以采用诸如匹配追踪(MP［9］)、正交匹配追踪(OMP［11］)、基追踪(BP［10］)、梯度投影法(GPSR［12］)、FOCUSS 等算法.因此便可以得到去噪图像

基于稀疏分解的图像去噪算法需要事先确定一个字典(即一组基或者一种变换)，使得图像在其上有足够稀疏的表达系数.用随意选取的固定字典近似表示任意自然图像精度很难保证.近年广受关注的基于学习的字典获取方法在一定程度上解决了这个问题.该方法从大量自然图像经过学习得到具有某种结构特征的字典，本文称之为单字典.从统计意义上来讲，这种单字典中部分原子的线性组合可以表示任意一幅与训练样本具有类似结构特征的自然图像.但是具体到某一幅图像或者某一类特殊的应用时，其针对性不强.考虑到图像复原问题中总会涉及同一幅图像的两个版本，如果学习所得的字典能够记录两个版本之间的对应关系，那么从观测图像估计原图将会具有更强的指向性，从而所估计的图像也会在结构上与原图更加接近.

2 基于多类型样本学习的联合字典

假定我们已经搜集大量某种类型的无污染的自然图像版本(下文简称X 版本)，对其模拟噪声干扰，再通过简单空间滤波得到所有图像的低质量版本(下文简称Z 版本)，然后通过这两类图像样本联合学习以获得字典.由于滤波处理有一定的抑制噪声的作用，但同时模糊了图像细节.因此我们预先提取低质量图像的结构特征作为复原图像结构特征的近似估计，以此建立低质量与高质量图像之间的结构关系.为此，采用式(1)的4 个特征提取算子对该Z 版本图像进行处理，即图像库中的每一幅X 版本图像，其Z 版本在4 个特征提取算子的作用下得到4 幅相应的图像Zi1，Zi2，Zi3，Zi4.若在图像Xi中以(i，j)为中心的邻域内采样，那么应该同时在相应的4 幅图像Zi1，Zi2，Zi3，Zi4中的相同位置采样.与单字典学习方法类似，若要分别以干净图像和经滤波处理的低质量图像为样本学习字典，可以采用以下形式的优化［27］(文献［13－14］证明了采用l1范数替换l0范数的合理性).

其中A，X 分别表示系数矩阵和样本矩阵.本文采用如图1 的采样方式，将上述所有样本顺次连接，即将(2)(3)式统一成(4):

其中n，m 分别表示从不同版本图像采集样本的维数.再利用K-SVD 算法求解该式，所得字典称之为联合字典.最后，按样本的组合方式对该联合字典进行拆分得到两个字典:Dclr，Dflt.由于此处所采用的样本来自于高质量图像块和相同位置低质量图像块的4 幅结构特征图像的组合，一幅图像相同位置应该具有同样的结构特征.由字典的学习过程可知，字典本质上是训练样本更紧凑的一种表示形式.图3 为本文训练所得的一个字典，可见其中包含指向不同方向的边缘.因此，采用这种方式搜集样本无疑可以帮助我们获得对拥有某类结构的图像更准确的表达.而且不难发现，通过一次训练获得的这两个字典不仅和单字典一样具有某类图像的结构特征，更重要的是它们之间具有该类图像不同版本之间的一种对应关系.另外，联合字典的学习过程表明一幅自然图像的两种版本X 和Z 被联合字典表示时共用一组表示系数.因此，当已知图像的Z 版本时，可以先将其在相应的字典Dflt上进行稀疏分解，所得系数与同时训练所得字典Dclr组合即可作为对原图的估计.图2 即为通过采用本文联合训练方法获得的一个字典的一部分.

图1 联合字典学习的采样过程Fig.1 Sampling process of joint-dictionary

图2 本文方法学习所得字典的Dclr部分Fig.2 A dictionary learnt with the method from this paper

现将多类型样本的联合字典训练算法总结如下:

(1)从不同版本的图像采样，初始化DC为高斯随机矩阵，并将矩阵的每一列规范化;

(2)采用匹配追踪算法求解下式，找到样本C 在字典DC上的分解系数A:

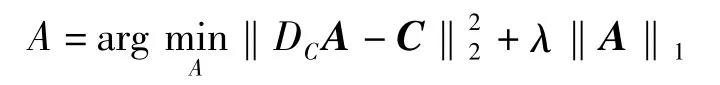
(3)用K-SVD 算法求解以下优化函数，得到联合字典DC:

(4)重复2，3 两步直到系数收敛到一组稳定值;

(5)按照样本的组合方式对所得联合字典进行拆分，得到所需要的两个字典，它们分别对应于不同类型的图像样本.

获得字典后，可以通过求解以下优化获得图像在该字典上的稀疏分解系数α:

其中F 同样是式(1)的4 个特征提取算子，需要保证处理方式与字典的训练过程一致.在实际操作中，为了避免优化函数的规模过大，以一定大小的图像块为单位进行估计，最后再将结果拼接整合得到最终的复原图像.如式(5)所示，在求每一个子图像块的表达系数时先对每一块提取特征，这一处理也包含了当前子块的邻域信息，所以部分重叠的依次处理图像中的每个子块后，它们能够很好的兼容在一起.现将基于联合字典的图像去噪算法流程总结如下.

算法:

(1)输入:离线训练的字典Dclr，Dflt以及噪声图像Y;

(2)对图像Y 做简单的滤波处理(本文分别采用了高斯滤波和双边滤波进行测试)得到低质量图像Z;

(3)以扫描顺序从左到右，从上到下部分重叠的依次选取图像Z 中的每一个k×k 的子图像块zi(i=1，2，…，n)(n 是子图总个数)，通过优化求得稀疏系数α;

(4)由xi=Dclrα，(i=1，2，…，n)得到对应的子图像块x，并将其放入去噪图像^X;

(5)重复3，4 两步直到Z 中所有子图像块被处理完.输出去噪图像^X.

3 实验结果与分析

本实验中，采用文献［8］中的图像库作为学习字典的训练集.分别采用高斯和双边滤波两种处理方式得到Z 版本图像，训练出相应的两组联合字典.对于训练图像采用以下参数获取相应的X 版本和Z 版本:高斯白噪声选择δ=25，高斯滤波处理的模板大小与选取的子图像块大小相同，本文所有实验都采用5×5 的子图像块，标准差为2(这个值越大平滑过后的图像越模糊)，双边滤波中控制颜色和距离的两个参数分别取为3 和0.2.采用如图1 的采样方式，从该图像训练集随机采集100 000 组子图像对样本用于离线训练超完备子典.从计算时间和图像质量两方面权衡，本实验字典的原子个数取512，即对应于X 版本图像的字典是25×512 的矩阵.表1 表示利用高斯滤波处理训练的字典和同样的预处理方式进行恢复结果.表2 表示利用双边滤波处理训练字典的恢复结果.两种情况下，本文方法都比单纯采用对应的滤波方法恢复的结果好.

表1 测试结果(PSNR:dB)Tab.1 Testing result(PSNR:dB)

表2 测试结果(PSNR:dB)(δ 表示噪声强度，σ 表示双边滤波的一个参数，值越大图像越平滑)Tab.2 Testing result(PSNR:dB)(δ is noise intensity，σ is a parameter of bilateral filtering，the bigger the image will be smoother)

在本实验有限的测试过程中，随着噪声强度的增大，通过调节滤波器的参数使其达到一定的平滑程度后，用本文方法恢复的去噪结果在PSNR 值上总可以比单纯的使用滤波方法高，但是从视觉上可接受的程度来讲，噪声强度太大导致损失掉的信息太多，此时无论什么方法都无法恢复出视觉上可接受的结果.图3 和图4 分别展示了不同噪声强度下利用高斯滤波作为预处理方法的去噪结果图像.从矩形框标记的部位可见本文方法在去噪的同时能够比单纯滤波更好的保持图像细节.图3 和图4 分别展示了不同噪声强度下利用双边滤波作为预处理方法的去噪结果.可见当噪声干扰较大的时候，尽管双边滤波可以通过调整参数控制图像的平滑程度，但过度平滑也是不可避免的，从而导致图像失真，这种情况下本文方法比单纯的双边滤波方法会使图像显得更加真实.

图3 第1 列表示δ=25 的噪声图像，第2 列表示高斯滤波的去噪结果，第3 列表示本文方法的去噪结果Fig.3 Column 1st are noisy images with δ=25，column 2nd are denoise results by gaussian filtering，column 3rd are denoise results from this page

图4 第1 列表示δ=50 的噪声图像，第2 列表示σ=［3，0，3］的双边滤波去噪结果，第3 列表示本文方法的去噪结果Fig.4 Column 1st are noisy images with δ=50，column 2nd are denoise results by bilateral filtering with parameter［3，0，3］，column 3rd are denoise results from this page

4 结论

本文提出采用联合字典学习的方法进行图像去噪.这种方法结合了字典训练能够学习获得图像的结构信息以及成对学习能够获取图像对之间的相关性这两者的优点.既能很好的提取图像的结构信息，同时学习得到的字典里包含的高、低质量图像对之间的关系也为我们提供了去噪图像的先验知识.从实验结果可见，本文方法在去噪的同时比单纯的滤波方法能够更好地保持图像的真实性.在某种意义上比一些传统的去噪算法更具优势.本实验同样启发我们相信通过对图像训练样本更有针对性的设计，本文方法同样适用于其他类似图像的复原问题.

［1］DONOHO D L，JOHNSTONE I M.Ideal spatial adaptation by wavelet shrinkage［J］.Biometrika，1994，81(3):425-455.

［2］DONOHO D L.De-noising by soft thresholding［J］.IEEE Trans Inf Theory，1995，41(3):613-627.

［3］COIFMAN R，DONOHO D L.Translation invariant de-noising［J］.In Wavelets and Statistics，Lecture Notes in Statistics，1995，125-150.

［4］STARCK J L，CANDES E J，DONOHO D L.The curvelet transform for image denoising［J］.IEEE Trans Image Proc，2002，11(6):670-684.

［5］ESLAMI R，RADHA H.Translation-invariant contourlet transform and its application to image denoising［J］.IEEE Trans Image Proc，2006，15(11):3362-3374.

［6］MATALON B，ELAD M，ZIBULEVSKY M.Improved denoising of images using modeling of the redundant contourlet transform［J］.it Presented at the SPIE Conf Wavelets，Jul，2005.

［7］ELAD M，AHARON M.Image denoising via sparse and redundant representation over learned dictionaries［J］.IEEE Trans Image Proc，2006，15(12):3736-3745.

［8］YANG J，WRIGHT J，HUANG T，et al.Image super-resolution via sparse representation［J］.IEEE Trans Image Proc，2010，19(11):2861-2873.

［9］MALLAT S，ZHANG Z.Matching pursuit in a time-frequency dictionary［J］.IEEE Trans Signal Proc，1993，41:3397-3415.

［10］CHEN S S，DONOHO D L，SAUNDERS M A.Atomic decomposition by basis pursuit［J］.Soc Ind Appl Math Rev，2001，43(1):129-159.

［11］PATI Y C，REZAIIFAR R，KRISHNAPRASAD P S.Orthogonal matching pursuit:Recursive function approximation with applications to wavelet decomposition presented at the 27th Annu［M］.Asilomar Conf Signals，Systems，and Computers，1993.

［12］FIQUEIREDO M A T，NOWAK R D，WRIGHT S J.Gradient projection for sparse reconstruction:Application to compressed sensing and other inverse problem［J］.IEEE J Selected Topics Signal Proc，2007，1(4):586-598.

［13］DONOHO D L.For most large underdetermined systems of linear equations，the minimal l1-norm solution is also the sparsest solution［J］.Commun Pure Appl Math，2006，59(6):797-829.

［14］DONOHO D L.For most large underdetermined systems of linear equations，the minimal l1-norm near-solution approximates the sparsest near-solution［J］.Commun Pure Appl Math，2006，59(7):907-934.