基于偏最小二乘法的锅炉飞灰含碳质量分数预测模型研究
葛彦鹏,崔 凝,董丽丽,杨 琛
(1.华北电力大学 能源动力与机械工程学院,保定071003; 2.天津大学 机械学院,天津300072)
电站锅炉效率与其排烟热损失、固体未完全燃烧热损失、灰渣物理热损失、可燃气体未完全燃烧热损失和散热损失有关[1],其中固体未完全燃烧热损失是锅炉的最主要热损失之一,仅次于排烟热损失。影响固体未完全燃烧热损失的因素多而复杂[2-3],其中飞灰含碳质量分数是一个重要因素。过高的飞灰含碳质量分数会对电厂的经济运行及安全生产造成许多不利影响,及时有效地获得其数据对机组运行人员调节机组状态有着重要意义[4]。
长期以来飞灰含碳质量分数数据的获得一直沿用传统的质量燃烧法[5],但此方法在时间上有很大的延迟性,很难及时地反映锅炉的燃烧运行状况,在安全生产上存在一定的隐患。因此对于飞灰含碳质量分数预测技术的研究显得格外迫切[6]。
偏最 小 二 乘 法 (PLS)是 由 S.Wold 和C.Albano等人于1983年首次提出[7],此方法是一种多因变量对多自变量的回归建模方法,较好地解决了许多以往用普通多元线性回归难以解决的问题,尤为重要的是当变量之间存在高度相关时,用偏最小二乘法进行建模,其分析结论更加可靠,整体性更强。而飞灰含碳质量分数的影响因素众多,各影响因素之间也是存在高度相关性,因此使用偏最小二乘法对其建立数学模型,并分析预测能达到很好的效果。
1 偏最小二乘法回归模型
在实际工作中,有一组因变量数据Y={y1,…,yq}(q为因变量个数)和一组自变量X={x1,…,xp}(p 为自变量个数)。
1.1 数据标准化处理
数据的标准化处理可以使新坐标系的原点与样本点集合的重心重合,并消除变量间的量纲差异,数据处理后不会改变其样本点间的相互位置及变量间的相关性。以自变量X为例,具体公式为:

处理后自变量数组记为E0=(E01,…,E0p)n×p,同理因变量数组记为 F0=(F01,…,F0p)n×q。
1.2 第一个主成分提取
t1是E0的第一个主成分,t1=E0w1;w1是E0的第一个轴,是一个单位向量,即‖w1‖=1。同样,u1是F0的第一个主成分,u1=F0c1,c1是F0的第一个轴,并且‖c1‖=1。为使t1、u1能很好地代表X、Y 中的数据变异信息,同时t1对u1有最大的解释能力,应使t1对u1的协方差(Cov(t1,u1))达到最大,即:
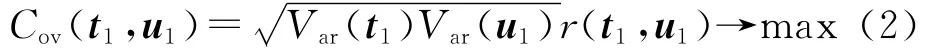
式中:Var(t1)、Var(u1)分别表示t1与u1的方差,r(t1,u1)表示t1与u1的相关度。
经推导有:
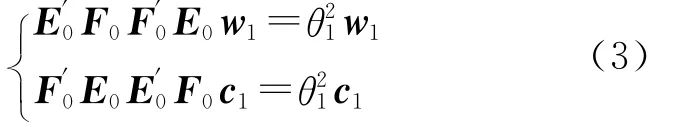
可见w1是矩阵E′0F0F′0E0的特征向量,其特征值是θ21。θ1是目标函数值,它取最大值时对应的w1是矩阵E′0F0F′0E0的最大特征值的单位向量。同样c1是对应于矩阵F′0E0E′0F0最大特征值θ21的单位特征向量。求得w1与c1后即可得主成分:

然后得回归方程:

式中E1、F*1、F1分别是三个回归方程的残差矩阵,方程回归系数为:
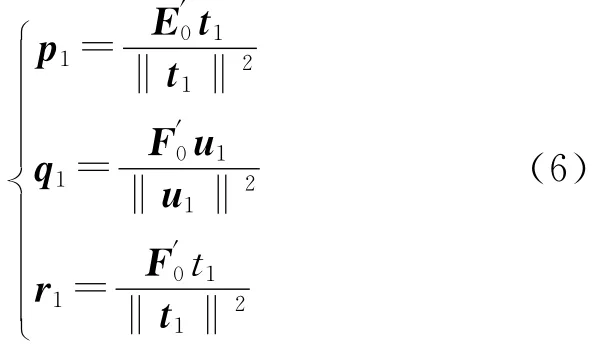
1.3 回归方程的拟合
数学原理及方法与第一个主成分的提取相同,用残差矩阵E1和F1分别取代E0和F0,求出第二个轴w2和c2及第二个主成分t2和u2。如果矩阵X的秩是A,则依次进行循环计算得到主成分t3,…,tA,则会有:
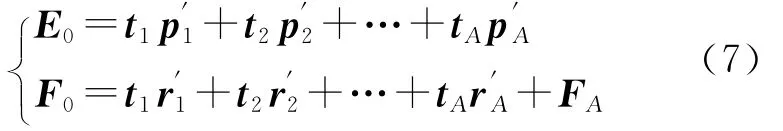
由于t1,…,tA均可以表示成E01,…,E0p的线性组合,上式可以变成y*k=F0k关于x*j=E0j的回归方程形式:

式中:k=1,2,…,q,FAk是残差矩阵FA的第k列。
1.4 交叉有效性
在偏最小二乘法回归建模中,为防止不充分拟合及过度拟合的发生,应确定合理的参与建模的主成分个数,目前广泛采用“舍一交叉验证法”选定建模的主成分个数。假设有n组样本点,先使用去掉第i组样本点所得样本集合(含n-i组样本点),并且用h主成分拟合一个回归方程;再将之前排除的第i组样本点带入拟合的回归方程,得到yi在样本点i上的拟合值^yhj(-i)。对于每一个i=1,2,…,n重复以上步骤,得到Y的预测误差平方和Bh(PRESSh,h=1,2,…,n):
当回归模型不稳定时,B的值就会增大,当B达到最小时模型的预测能力最好,则选择对应的h个主成分拟合方程。
2 飞灰含碳质量分数预测模型
2.1 数据样本
影响飞灰含碳质量分数的因素众多,本文选取了发电负荷、总煤量、一次风压、二次风压、排烟温度、省煤器出口烟温、燃尽风风门开度、烟气含氧体积分数等8个因素(x1~x8)作为输入变量,利用内蒙某电厂2011年6月的运行数据进行计算,从中选取具有代表性的40组数据作为样本建立预测模型,15组数据用于模型精度的检验。建模数据见表1,检验样本见表2。
2.2 预测模型的建立
经“舍一交叉验证法”计算的B值见表3。
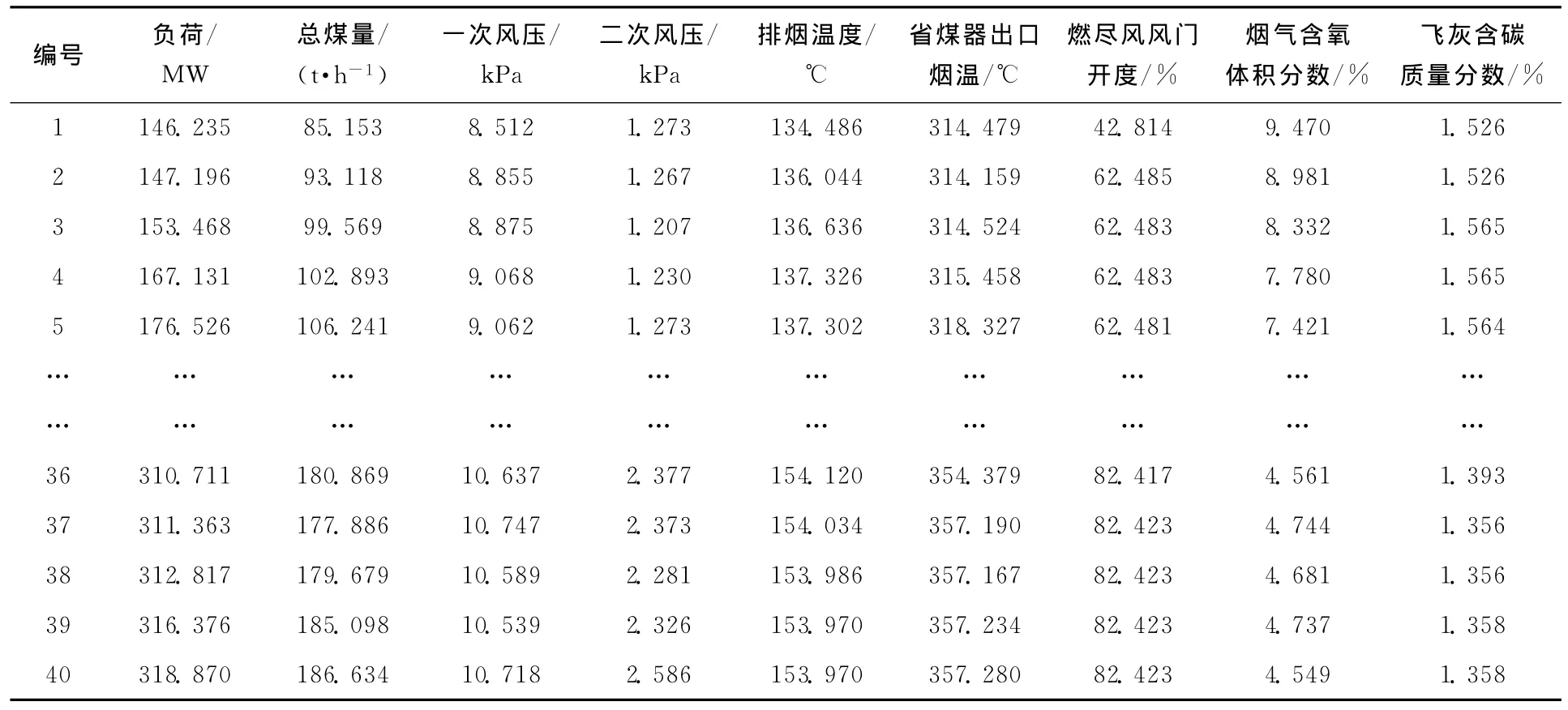
表1 飞灰含碳质量分数建模数据
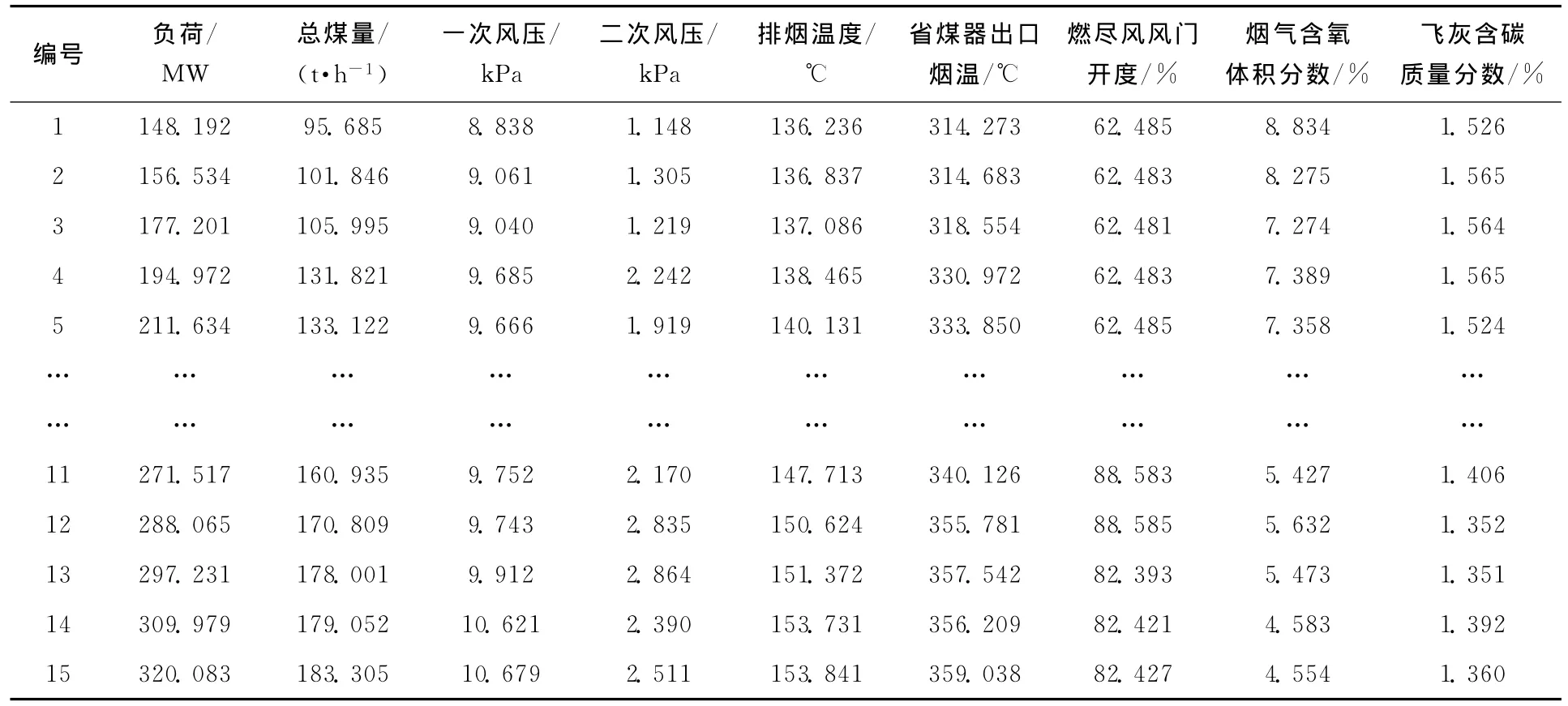
表2 飞灰含碳质量分数检验数据
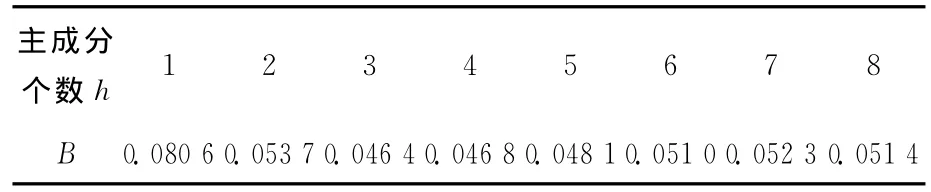
表3 舍一交叉验证表
从表3可以看出:当主成分个数h=3时,B值最小,所以选择提取3个主成分建立预测模型,得到偏最小二乘回归模型。回归方程如下:
(1)标准化变量回归方程为:

2.3 模型精度检验与分析
2.3.1 变量投影重要性指标
为了分析自变量与因变量之间的相关性关系,这里使用变量投影重要性指标Dj(VIPj,Variable important in projection)来测度各因素对于因变量影响的大小。其定义式为:
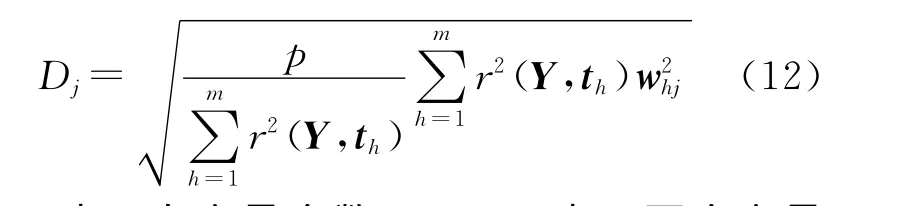
式中:p表示自变量个数;r(Y,th)表示两个变量的相关系数;whj是轴wh的第j个分量。对于各自变量,如果它们在解释因变量Y时的作用相同,则所有的Dj均等于1;对于Dj>1的自变量xj,它在解释Y时就有更加重要的作用。
根据上述偏最小二乘回归模型,绘制变量投影重要性指标图(见图1),从中可以看出各个因素对于因变量的影响程度。
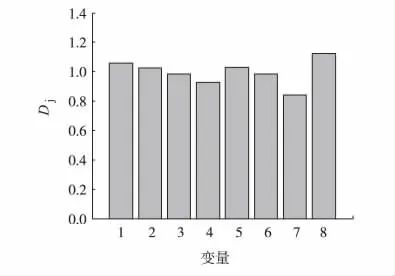
图1 变量重要性指标投影图
从图1可以看出:8个因素中烟气含氧体积分数对于飞灰含碳质量分数的影响最大,燃尽风风门开度对其影响最小,整体来说各因素的Dj值均接近于1,所以选取的影响因素比较恰当。
2.3.2 数据检验与分析
为了分析模型的回归效果,给出40组建模数据样本的预测值与实际值对比图以及相对误差图,见图2与图3。
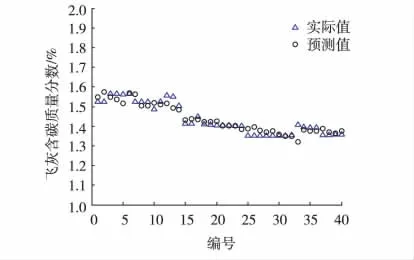
图2 建模数据实际值/预测值对比曲线
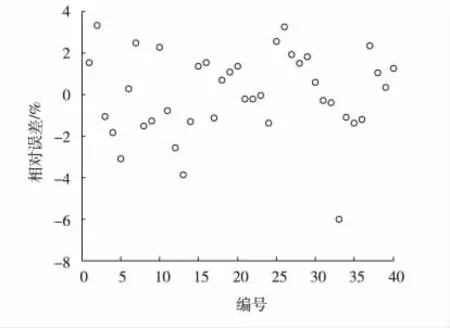
图3 建模数据相对误差曲线
从图3可以看出:绝大多数样本点的预测值相对误差在3%以内,整体来说回归模型对于因变量的拟合效果很好。
为了进一步检验飞灰含碳质量分数回归模型的精确有效性,使用15组检验数据进行飞灰含碳质量分数的预测,结果见图4与图5。
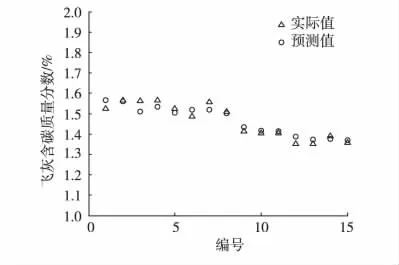
图4 检验数据实际值/预测值对比曲线
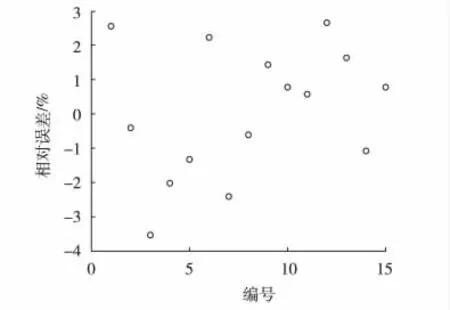
图5 检验数据相对误差曲线
从检验样本的预测结果不难看出,预测值相对误差依然控制在3%以内,模型预测精确性较高。
3 结语
电站锅炉飞灰含碳质量分数的影响因素众多,各因素间存在较高的相关性,本文使用偏最小二乘法可以很好地克服变量间的多重相关性影响,其计算结果的精确性也很高,模型预测结果可以很好地代替实际测量值。因此,偏最小二乘回归法适合飞灰含碳质量分数的预测,具有很强的可行性。
[1]樊泉贵 .锅炉原理[M].北京:中国电力出版社,2004.
[2]王凯.基于遗传算法-BP神经网络的飞灰含碳量和NOx的研究[D].北京:华北电力大学,2009.
[3]罗春雷 .基于BP网络的锅炉优化燃烧指导系统[J].中国电力,2001,34(10):59-61.
[4]杨国强 .反向建模方法在电站锅炉飞灰含碳量测量中的应用[D].北京:华北电力大学,2009.
[5]周新刚 .燃煤电站锅炉飞灰含碳量预测模型研究[D].济南:山东大学,2006.
[6]陈敏生,刘定平 .基于核主元分析和支持向量机的电站锅炉飞灰含碳量软测量建模[J].华北电力大学学报,2006,33(1):72-75,92.
[7]王惠文.偏最小二乘回归方法及其应用[M].北京:国防工业出版社,1999.
——与非适应性回归分析的比较

