关于复变函数与积分变换教学的几点注记

王焱平

(上海电力学院 数理学院，上海201319)

1 关于幅角与多值函数

我们知道，复变函数中的多值函数大多是由幅角函数

w=Argz=argz+2kπ(k∈Z，这里Z代表整数集)

引起.幅角函数具有性质：

Argz1z2=Argz1+Argz2.

这里，等号代表两个数集相等，加法代表两个数集的加法：A+B=x+yx∈A,y∈B.

例如：A=B=1,2,C=2,3,4，则C=A+B=A+A，2A=2,4，可见A+A≠2A.同理，

Argz2=Argz+Argz≠2Argz.

另外注意，对主幅角argz函数，性质：

argz1z2=argz1+argz2

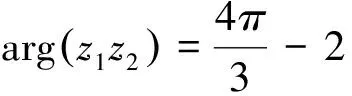
由此可知，复对数函数w=Lnz=lnz+iArgz虽具性质：

Lnz1z2=Lnz1+Lnz2，

但

Lnz2=Lnz+Lnz≠2Lnz

又对它的任一个单值分支，w=lnz=lnz+iargz+2kπ(k为某个整数)，性质：

lnz1z2=lnz1+lnz2

也不再成立.

我们知道，反三角函数可用对数函数表示，例如，容易知道，

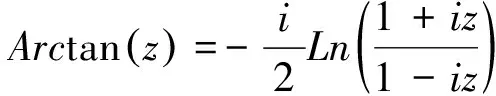
于是

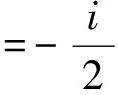
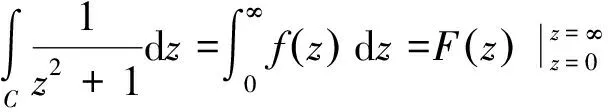
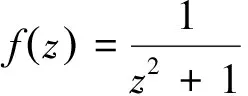
2 关于柯西积分公式、高阶导数公式及留数定理

柯西积分公式和高阶导数公式可以作为留数定理的推论.对工科学生来讲，重要的是尽快掌握数学的基本概念理论及应用方法，应该不要像数学专业的学生一样太在意定理或公式证明的过程及从逻辑上计较应该谁在先谁在后.基于这样一个想法，这里把柯西积分公式和高阶导数公式放在留数定理后面介绍，作为留数定理的推论，可使整个结论统一起来，避免重复，又便于减轻学生的学习负担及抓住学习的重点.

留数定理：设复变函数fz在简单闭曲线C上连续，在简单闭曲线C内部有有限个孤立奇点z1,z2,…,zn，则

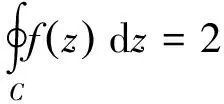
证明可利用复合闭路定理和留数的定义(略).由孤立奇点的分类及孤立奇点留数的计算法则知柯西积分公式及高阶导数公式可作为该定理的推论.如下所述.

推论1：设复变函数fz在区域D解析，简单闭曲线C及其内部均在D中，则对C内部的任一点z0，有

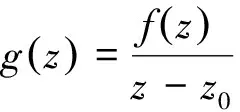
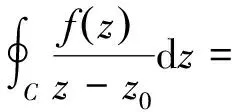
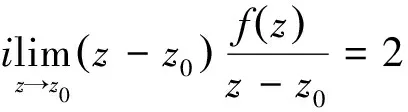
即

证毕.

推论2：设复变函数fz在简单闭曲线C及其内部区域D解析，则fz在区域D内有任意阶解析的导函数，且有高阶导数公式：

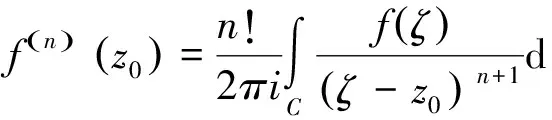
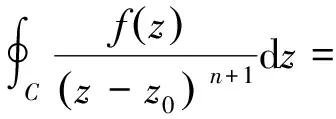
证毕.

3 关于广义δ-函数

许多同学单从以下表达式来理解广义δ-函数：

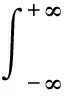
定义：设R为实数集，S=fxfx:R→R是一个函数，有任意阶导函数是一些函数构成的集合，定义一个集合映射

δx:S→R，使得∀fx∈S，δx:fx↔f0，

即δxfx=f0.称δx为广义δ-函数(简称为δ-函数).

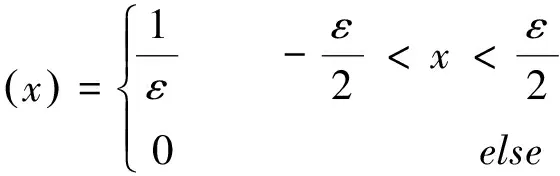
先给出一个引理，证明很简单，这里略去.

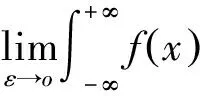
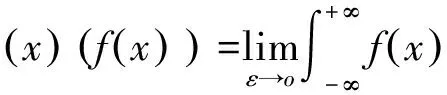
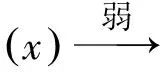
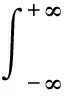
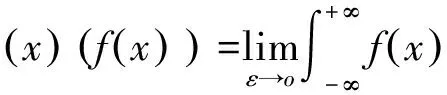
利用函数族δεx，还可定义δx-x0为

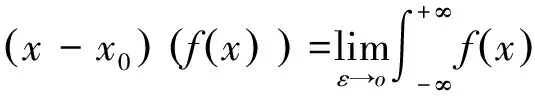
则由定积分的变量替换公式我们有

故δt-t0在信号与系统中用于表示对信号在时刻t=t0采样.

利用函数族δεx，还可定义δax为

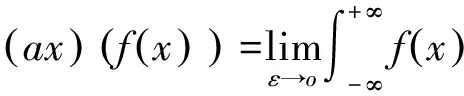
于是，由定积分的变量替换公式我们有

故信号与系统中，δax用于表示对采样信号的增强或减弱.

特别，取a=-1 则有δ-x=δx，故也称广义δ-函数为偶函数.

类似可定义δ-函数的导函数δ′x：δ′xfx=-f′0，∀fx∈S,

综上所述，由于我们将δ-函数的作用写成积分形式，所以一定要告知学生，出现δ-函数只有通过积分才有意义.δx本身只是一个符号(正象正弦函数sinx中的sin是一个符号一样)，它只有作用在自变量fx∈S上才能表现出来，即

参考文献：

[1]Ahlfors L V.Complex Analysis (Third Edition)[M].McGraw-Hill Companies，1979.

[2]钟玉泉．复变函数[M]．北京：人民教育出版社，1980.

[3]方企勤．复变函数教程[M]．北京：北京大学出版社，1996.

[4]西安交通大学高等数学教研室．复变函数(第四版)[M]．北京：高等教育出版社，1996.

[5]刘子瑞，梅家斌．复变函数与积分变换[M]．北京：科学出版社，2007.

[6]陈恕行．现代偏微分方程导论[M]．北京：科学出版社，2005.