多尺度网格细胞路径综合方法

邰能建 吴德伟 戚君宜 周 阳

（空军工程大学 信息与导航学院，西安710077）

动物能利用空间运动信息实现路径整合（Path Integration），该整合依赖于大脑内部机制，能够在不使用外界环境条件下实现路径计算.动物神经学家经研究发现，啮齿动物大脑内的海马（hippocampus）在导航中起着关键性作用，认为海马能够实现“空间认知图”，并且在路径整合中发挥重要作用，但并不具有路径整合器功能.文献［1］确定了路径整合器在脑结构中的解剖位置，其有力证据是在脑背侧内嗅皮层（dMEC，dorsal Medial Entorhinal Cortex）发现对空间特定方位具有放电特性的网格细胞（grid cells），动物在空间处于任一节点位置，网格细胞都能产生一定大小的放电野（firing field）.2010年发表在 Nature的文章中［2］也证实了人脑中网格细胞的存在.研究者认为网格细胞是动物空间导航系统的重要组成部分，并被证实具有路径整合器功能［1］，其网格式的放电结构使得内嗅皮层（MEC，Medial Entorhinal Cortex）与环境空间形成紧密对应关系［3］.国内牟炜民等人［4］指明了人类空间巡航与空间记忆的内在机制有关.于平等人［5］在对网格细胞在空间记忆中作用的综述中，也指出空间记忆中所发挥的路径整合器功能.但目前尚未发现有关模拟网格细胞路径整合器功能的国内外文献公开发表.对网格细胞路径整合器功能进行模拟，不仅利于探索网格细胞实现路径整合器生物机制，还将有助于无人作战飞机（UCAV，Unmanned Combat Aerial Vehicle）的空间认知自主导航［6］研究.本文将在分析网格细胞形成机制的Burgess模型基础上，模拟网格细胞特性，提出一种多尺度网格细胞路径整合方法，并对其性能进行仿真验证.

1 网格细胞介绍

网格细胞在特定空间位置发生重复性的放电，多个放电空间相互交叠形成网格节点，连接网格节点便形成以等边三角形为基本结构的网格.网格细胞的放电野具有4个基本参数［1］：①间距，各节点间的距离；②方向，网格相对于参考坐标系的旋转角度；③位相，网格相对于参考点的位移；④放电野大小，空间放电范围.总体而言，网格细胞主要具有以下特点［1］：

1）对于dMEC区相同位置记录到的网格细胞，其放电野具有相同的间距、方向、放电野大小等特征，但位相各不相同.在空间范围扩大时，网格结构及节点间的距离不会改变，但网格节点的数量不断增多.

2）MEC具有大量的网格细胞集群，每个细胞集群具有相同的网格间距和方位，相邻细胞集群间的位相具有连续性，而细胞集群中网格细胞位相则随机变化.从MEC的背侧到腹侧，网格细胞间距（39～73cm［1］）和放电野呈递增性变化.

3）网格细胞形成的放电野具有稳定性.若将外部环境空间旋转一定角度，网格图旋转相同的角度，而间距和放电野大小并没有改变.在黑暗条件下结论相同.

2 网格细胞形成机制的模拟方法

目前网格细胞放电野的形成机制模拟研究集中于文献［7］提出的振荡干扰模型，将动物躯体信息的theta波振荡与各头朝向细胞的theta波振荡进行整合，经过调整得到空间线形振荡波，通过交叉整合多个线形振荡波便得到等边三角形密布的网格结构图，网格节点即为波峰重叠点，其基本表达式为

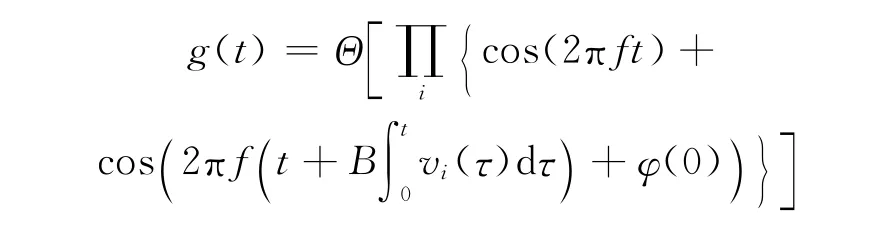
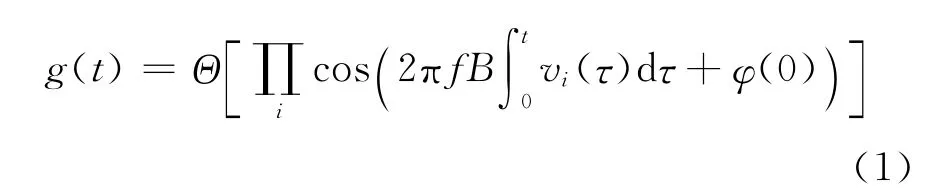
上式发现，通过多个振荡频率叠加，若g（t）值超过门限值（式中为0），各网格细胞的响应程度相同，因此Burgess模型只能模拟网格细胞的形成机制.并且该模型中头朝向细胞的方向及个数决定了网格细胞放电野的形成，文献［7］采用0°，120°，240°3个方向进行模拟，文献［8］也采用30°，90°，330°3个方向.

3 基于网格细胞的路径整合方法

本文在Burgess模型基础上，提出一种基于多尺度的网格细胞路径整合方法，模拟网格细胞的空间特性，构建一组尺度d连续变化的网格图组，在各层网格图中引入突触样式（synaptic pattern）模拟动物当前空间位置在网格层中的对应位置，依据各层细胞活跃度的变化进行动物的路径整合，示意图见图1，实现方法主要包括两部分：多尺度网格图组构建及路径整合实现.

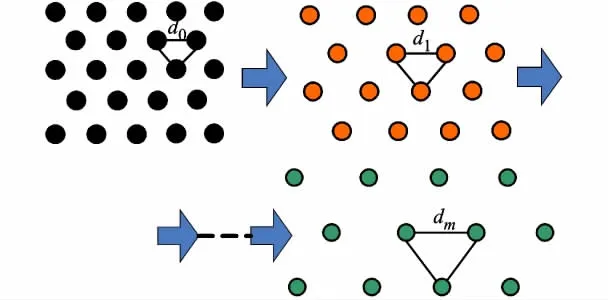
图1 多尺度网格细胞示意图，自左向右尺度逐渐增加

3.1 多尺度网格图组构建

1）设置尺度参数dm，用Burgess模型计算各网格层的网格细胞空间分布图.由于相同尺度的不同网格细胞间只是位相不同，而不同网格细胞的相互叠加最终构建全部环境的网格细胞放电野，因而设定构建的各层网格足够大以覆盖全部环境空间.设在区间内总层数为M，则各层尺度表示为式（1）给出的Burgess模型虽不包括尺度参数dm，但调整参数B 与dm存在转换关系［8］：B＝2／

2）对各层的网格细胞进行以下步骤的计算：

步骤① 计算各细胞的活跃度Bi（t＋1）.若设第i个细胞在t＋1时刻的活跃度为Ai（t＋1），则

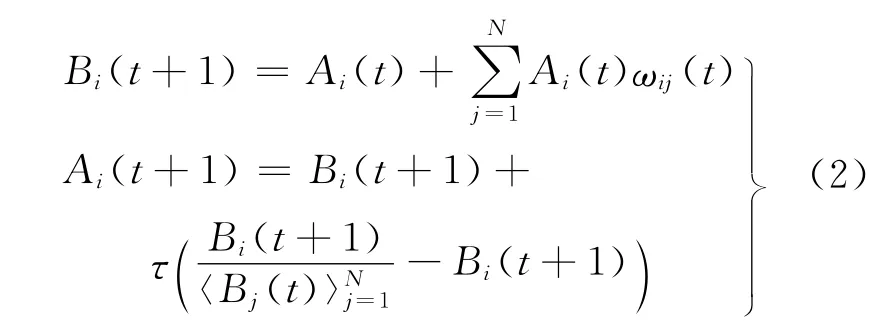
其中，N为细胞总数；ωij（t）为相互间联系权值；为各层网格中所有细胞活跃度的均值，可通过增添一个细胞（不属于网格细胞）实现；参数τ用于决定细胞间联系的强弱.为防止权值出现负值，设定

1.关于核心素养的研究。2013年，我国成立了“学生发展核心素养”联合课题组，由北京师范大学等多所高校的近百名研究人员组成。2016年9月13日上午，中国学生发展核心素养研究成果发布会在北京师范大学举行。《中国学生发展核心素养》指出：学生发展核心素养是指学生应具备的，能够适应终身发展和社会发展需要的必备品格和关键能力。“中国学生发展核心素养”共分为文化基础、自主发展、社会参与三个方面，综合表现为人文底蕴、科学精神、学会学习、健康生活、责任担当、实践创新6大素养。

步骤② 突触计算.突触包括用于计算平均活跃度的突触及模拟动物空间位置响应程度的突触.对于前者，各层网格细胞都用到活跃度均值，因此各细胞与均值细胞间的联系权值都为1；而后者需要模拟位置响应程度，借鉴位置细胞活跃度的模拟方法，本文采用包括相对幅值I、抑制幅值T及方差σ3个参数的高斯函数计算权值，既增强相邻间细胞的联系权值，又能抑制较远距离细胞的权值，各细胞间的联系权值ωij（t）满足：

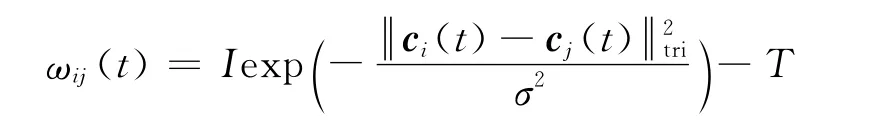
步骤③ 计算突触样式在各层网格图中的移动.突触样式的移动与动物在空间移动密切相关，以运动速度v（t）＝（vx（t），vy（t），vz（t））T为输入量，突触样式在网格中的移动与v（t）的对应关系为

其中，αm（t）为第m层网格与空间位置的转换比例，d0为网格尺度dm对应的空间距离，各网格层d0相同，由于αm（t）＝dm／d0，则αm（t）与dm成正比关系；φ 为v（t）在（vx（t），vy（t））网格平面上的夹角；β∈［0，3π］为网格旋转偏移量，则权值变化为

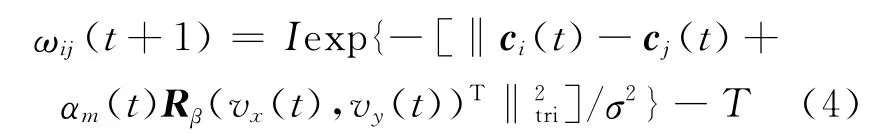
3）重复步骤②，直至所有层网格构建完成.

3.2 路径整合实现

2）确定网格与空间位置的转换比例αm（t）.在M确定时，可通过初始尺度d1及尺度步进间隔Δd，利用dm＝0.39＋（m－1）Δd计算各层的尺度，进而在设定地理空间距离d0基础上，计算各层与空间位置的转换比例；

3）设定突触样式参数，设定网格旋转偏移量β、速度v（t）＝（vx（t），vy（t），vz（t））T；

4）利用式（4）在各网格层依次计算不同时刻的突触权值，利用式（2）计算细胞的活跃度，记录最大活跃细胞在ti时刻的网格位置变化量计算网格位置与前一时刻位置的相对方向Δθi.由于网格方位与地理空间方位一致，因而基于网格细胞路径综合实质是通过计算网格位置变化量及方位变化量Δθi计算ti时刻网格位置与在各层网格的相对位置，最终利用转换比例αm（t）推算ti时刻的地理空间方位：

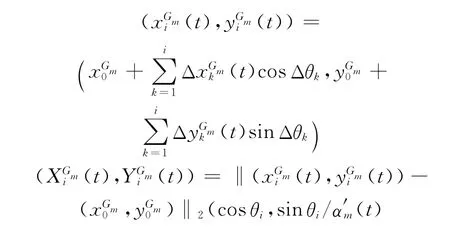
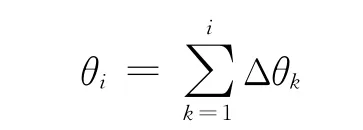
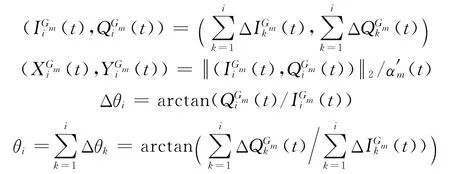
5）每隔时间T0，利用低尺度路径整合的结果调整高尺度路径整合，提高空间位置的整合精度.

4 网格细胞路径整合方法仿真测试

本文以UCAV为研究对象，测试基于多尺度网格细胞路径整合方法.测试内容包括：①相同条件下不同尺度对路径综合精度的影响；②利用低尺度路径整合结果调整高尺度的性能；③俯冲、爬升对路径整合精度的影响；④方向精度，基本参数：起始位置（X0，Y0）＝（0，0），vx（t）＝50m／s，速度误差dvx＝6m／s，方向误差dk＝6°，φ＝0；M＝8，则dm＝0.39＋0.04（m－1），m∈｛1，2，…，8｝；d0＝100m，则αm（t）＝（0.39＋0.04（m－1））／100；空间环境没有变化，即β＝0；高斯函数参数I

4.1 不同尺度网格的路径综合精度

图2给出了不同尺度网格中的路径综合随时间变化关系，时隙Tstep＝10.可见，随着时间增加，X轴及Y轴方向的误差呈线性增长，并且尺度越大，误差斜率越大；但易验证，在利用式（3）向空间位置转换后，各层误差的结果相同，因为各网格空间的速度与αm（t）呈正比例关系，但式（3）通过除以αm（t）进行位置转换，αm（t）影响量相抵消.还可验证，速度误差与方向误差满足时，本文方法能精确推算UCAV空间位置.

4.2 低尺度对高尺度调整后的路径整合精度

通过图2的仿真结果还可看出，若在网格空间利用低尺度的路径整合结果在时间T0后对高尺度结果进行调整，可提升空间地理位置的整合精度.考虑：①被调整的尺度层越高，整合误差调整幅度越大，因此可对最大尺度层的整合结果进行调整；②网格空间内，基本尺度的路径整合与高尺度路径整合误差幅度满足（m－1）Δd关系，其中，m为高尺度所在层数，Δd＝■ψ／M」为尺度递增幅度.本文调整方法是：在各调整时刻，对高尺度路径整合结果沿X轴方向减去（M－1）Δd、沿Y轴方向减去调整后结果见图3.本文的方法既能保证网格空间各层整合精度与最高精度（d1层精度）相近，也能一定程度上提高地理空间的整合精度.

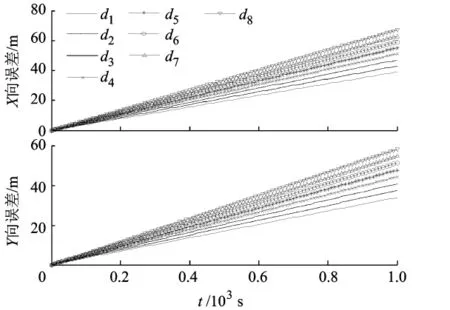
图2 不同尺度网格的路径综合网格中误差

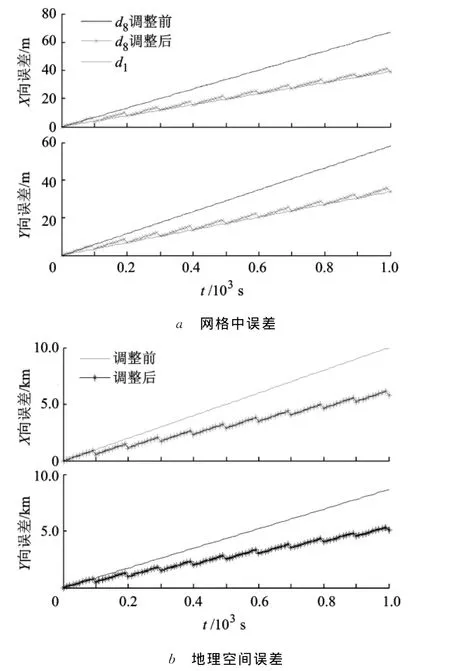
图3 调整后的路径综合性能

4.3 爬升对路径整合精度的影响

由于速度相同时，俯冲与爬升过程的区别在于Z轴方向速度分量符号相反、数值相同，因此本文仅对爬升过程进行研究.设定UCAV在爬升过程中以v（t）＝50m／s飞行，且无Y 轴方向分量.图4给出了基本尺度网格层在φ∈［0，π／6］时的路径综合结果.通过图4中X向误差可看出，由于爬升角度增大，X轴相同时间差网格移位量减小，精度并无变化规律.由于各角度的转换比例相同，因此地理空间误差的变化规律相同.在应用时，可对各层的整合结果取平均用于导航.易验证，其他尺度的误差规律相同.

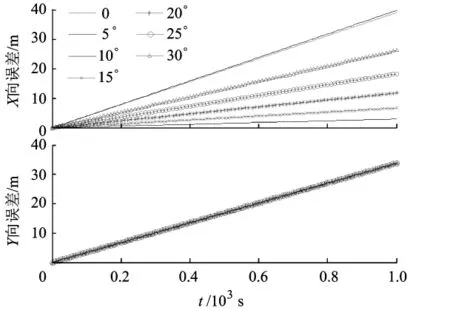
图4 爬升过程中网格路径综合误差

4.4 方向精度

设定UCAV沿以v（t）＝50m／s水平飞行、速度误差dv＝6m／s、方位为k＝π／10条件下，易验证各尺度的方向误差相同，并且不随时间变化.图5给出了不同方向对应的误差值分布，可见，在相同网格沿不同方向进行方向推算，除在k＝0，π／3，π／2时误差基本为0外，误差值随方向角度变化呈锯齿状分布；易验证，方向误差也与速度、速度误差相关.

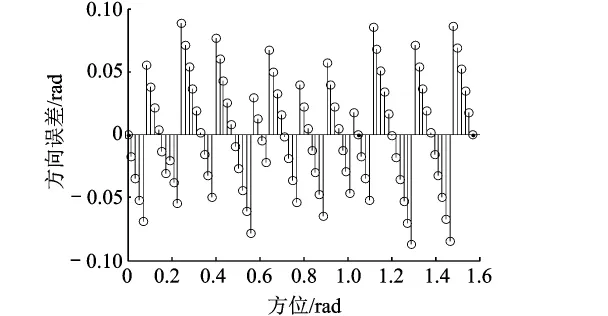
图5 不同角度的方向精度

5 结 束 语

为模拟生物网格细胞的路径整合器功能，本文在Burgess模型基础上，提出了一种多尺度网格细胞路径整合方法：首先构建了一组各层尺度递增的多尺度网格图组，并在各层中引入突触样式计算各细胞权值，依据细胞活跃度的变化进行路径整合.主要结论有：

1）一定范围内的速度误差与方向误差范围内，本文方法能精确推算方位；

2）不同尺度网格的空间位置路径综合精度相同，但网格空间的精度不同，尺度越大，误差越大；

3）在网格空间利用低尺度整合结果对高尺度结果进行调整，能较大改善空间位置的推算精度；

4）对于以相同速度、不同角度爬升的UCAV，各层推算精度与角度变化无固定关系；

5）各层的方向误差相同，相同网格沿着不同方向推算的方位精度不同，误差值与方位、速度及速度误差值相关.综上所述，本文能够为UCAV认知导航研究提供一种有效的网格细胞路径整合方法.

（References）

［1］Hafting T，Fyhn M，Molden S，et al.Microstructure of a spatial map in the entorhinal cortex ［J］.Nature，2005，436：801－806

［2］Doeller C F，Barry C，Burgess N.Evidence for grid cells in a human memory network［J］.Nature，2010，463：656－661

［3］Witter M P，Moser E I.Spatial representation and the architecture of the entorhinal cortex ［J］.Trends in Neurosciences，2006，29（12）：671－678

［4］牟炜民，赵民涛，李晓鸥.人类空间记忆和空间巡航［J］.心理科学进展，2006，14（4）：497－504 Mou Weimin，Zhao Mintao，Li Xiaoou.Human spatial memory and spatial navigation［J］.Advances in Psychological Science，2006，14（4）：497－504（in Chinese）

［5］于平，徐晖，尹文娟，等.网格细胞在空间记忆中的作用［J］.心理科学进展，2009，17（6）：1228－1233 Yu Ping，Xu Hui，Yin Wenjuan，et al.The roles of grid cells in spatial memory ［J］.Advances in Psychological Science，2009，17（6）：1228－1233（in Chinese）

［6］吴德伟，邰能建，戚君宜.基于认知理论的UCAV智能导航研究新进展［J］.空军工程大学学报：自然科学版，2011，12（4）：52－57 Wu Dewei，Tai Nengjian，Qi Junyi.A new research progress of UCAV intelligent navigation based on cognitive theory［J］.Journal of Air Force Engineering University：Natural Science Edition，2011，12 （4）：52－57（in Chinese）

［7］Burgess N，Barry C，O’Keefe J.An oscillatory interference model of grid cell firing［J］.Hippocampus，2007，17（9）：801－812

［8］Zsófia Huhn，Zoltán Somogyvári，Tamás Kiss，et al.Distance coding strategies based on the entorhinal grid cell system［J］.Neural Networks，2009，22（5／6）：536－543