基于M／M／1模型的网络及时可靠性加速模型

李瑞莹 康 锐 黄 宁

（北京航空航天大学 可靠性与系统工程学院，北京100191）

随着网络技术的不断发展与应用，对网络的定量与定性特征的科学理解，已成为一个极其重要的挑战性课题，甚至被称为“网络的新科学”［1］.随着网络使用的普及，网络负载增大，由拥塞造成的及时可靠性已经成为网络定量特征理解的重要问题.

在一个新的网络建成前，在一种新的服务投入使用前，试验是考核网络可靠性的重要途径.然而，网络任务周期普遍较长，为了有效暴露故障，网络可靠性试验时间往往是其任务周期的数倍［2］，这直接导致研制周期过长，对基于长时间效应的传统可靠性试验技术提出了挑战.1967年，美国罗姆航空发展中心提出了加速寿命试验（ALT，Accelerated Life Testing）方法［3］，使高可靠长寿命产品可靠性水平的快速评定成为可能，并广泛应用于航空航天、武器装备及机械电子等领域［4］.为了快速在可靠性试验中暴露设计缺陷，确定网络可靠性水平，也有必要采取加速试验，增大单位时间内的循环次数，加速故障模式的出现.

文献［5］提出故障过程的加速性是设计加速试验的前提，即要求在保持产品故障机理不变的情况下，产品可靠性特征参数与应力之间存在一个确定的函数关系，称为加速模型［6］.网络服务层的应力主要体现为工作应力，即用户对网络服务的使用，也就是网络的负载或数据包的到达.网络及时可靠性的故障模式为时延过长，网络的排队机制［7］为探索延迟故障机理以及确定加速模型提供了支撑，典型的通信网络排队机制包括M／G／1，M／M／1，M／D／1，M／M／C，D－MAP／PH／1，DBMAP／PH／1［8－9］等.相似理论［10］是确定加速模型的理论依据，如文献［11］在对混凝土结构的耐久性试验中，分析了混凝土结构在室内加速试验环境与现场自然环境条件下性能退化的时间相似关系，提出多重环境时间相似理论；文献［12］对加速试验中起关键作用的时间相似的各类情况进行了讨论.流体力学是相似理论的重要应用领域［10］，对于通信网络而言，网络中数据也是一种流体，数据的流动也需要服从相应的规律，即排队机制.文献［13］结合运动相似和力相似的原理，采用拓扑结构简化、网络流合并等技术给出了一种网络可靠性相似建模的初步方案，但其对网络建模粒度较粗，没有考虑网络流量与服务机制的影响，同时对相似性实现原理研究不够深入，缺乏相应的模型验证.

本文以相似理论为理论基础，研究通信网络最简单的排队模型——M／M／1模型对应的网络及时可靠性加速模型，并通过OPNET仿真平台进行验证.

1 基本概念

网络可靠性是指网络在规定条件下和规定时间内完成规定功能的能力.由于网络使用量日益剧增，网络可靠性研究焦点已集中到“及时可靠性”，即网络能否及时地传输信息，其故障判据是网络端到端传输时延超过用户容许范围，及时可靠度可以表达［14］为式中，D（t）表示t时刻的网络端到端传输时延；Dmax表示用户允许的最大时延，也就是故障判据.

网络端到端时延包括4个部分，即：处理时延Tp、传输时延Tt、传播时延Tg和排队时延其中，前三者均取决于节点处理速度和信道传播速度，且量值与排队时延相比很小，因此对网络端到端时延影响最大的是排队时延，主要因素包括链路的负载情况、队列管理机制、缓冲区管理机制、接口处理能力等.

试验中，网络及时可靠度的统计方法为

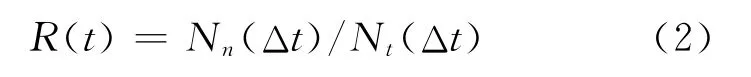
式中，Nt（Δt）表示t时刻以后的Δt时间段内网络传输的数据包总个数；Nn（Δt）表示t时刻以后的Δt时间段内网络传输时延不超过用户允许的最大时延Dmax的数据包个数，也就是传输及时的数据包个数.

2 故障机理分析

常见的通信网排队模型包括 M／M／m（n），M／D／m（n），M／Er／m（n）等［16］.M／M／1模型是以太网交换机的初级应用，其表达的含义为：网络数据到达时间间隔服从参数为λ的负指数分布，服务时间服从参数为μ的负指数分布，服务台数为1，无损失，服务机制为先到先服务，其排队过程如图1所示.

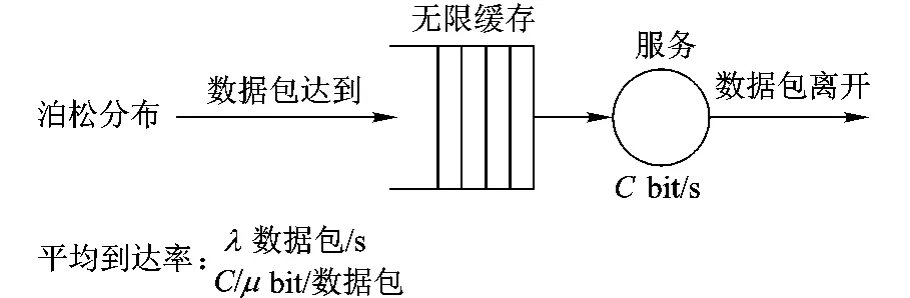
图1 网络通信M／M／1排队过程

在M／M／1的排队系统中，网络数据包到达后，如交换机空闲，则开始提供数据交换服务，否则排队等待，直到前面所有的数据包完成数据交换.如果等待时间过长，达到故障判据，则发生延迟故障.

对于M／M／1排队系统，有两类情况，当系统服务强度ρ＝λ／μ＜1时，系统能达到统计平衡，网络排队时延随时间变化如图2a所示；否则，数据到达累积会越来越多，系统无法达到稳态，网络排队时延越来越长，其随时间变化如图2b所示.

因此，这里只分析服务强度ρ＝λ／μ＜1的情况.ρ＝λ／μ＜1时，数据包在服务系统中的逗留时间分布函数为［7］

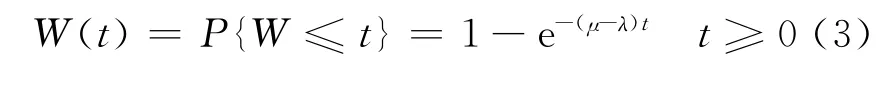
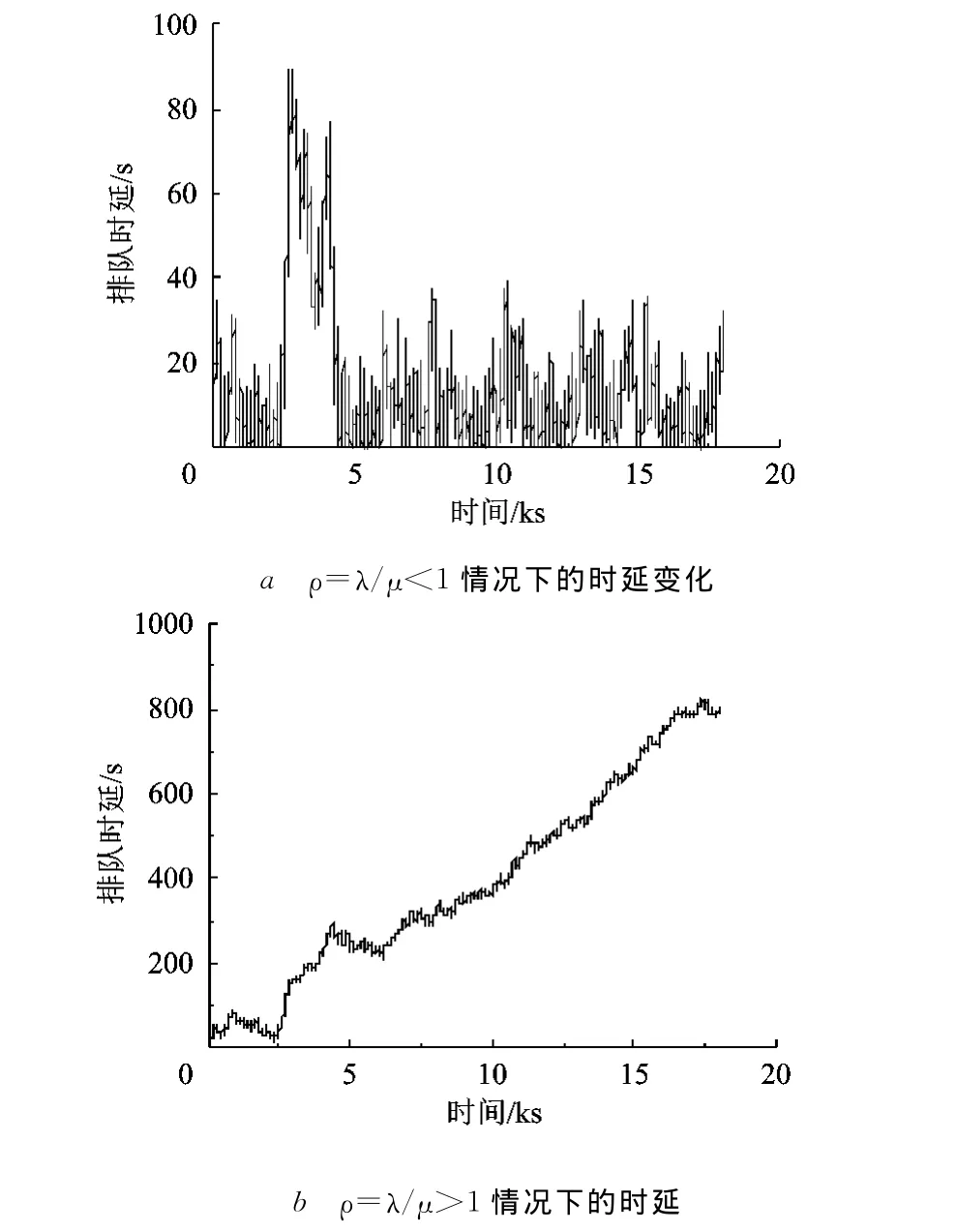
图2 不同服务强度下M／M／1系统的排队时延

式中，W（t）是数据包的逗留时间，为等待时间与服务时间之和.实际上，这就是通信网络及时可靠度的表达式.式（3）中，t就是给定的时延阈值Dmax.结合式（2）和式（3），网络及时可靠度可以表达为

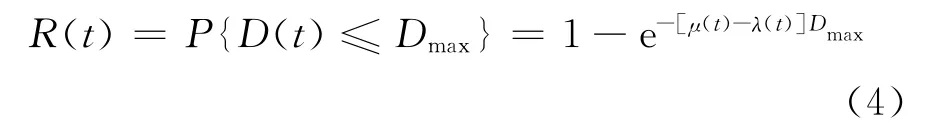
式中，μ（t）表示t时刻的网络平均服务时间；λ（t）表示t时刻的平均数据到达时间间隔；Dmax表示用户允许的最大时延.

3 基于相似理论的加速模型

下面针对式（4），采用相似理论的方程分析法推导加速模型.令原始现象为

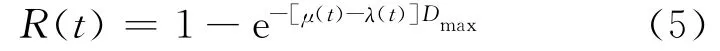
相似现象为

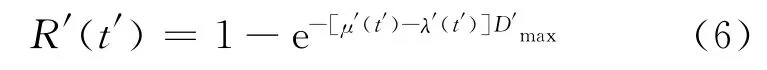
式（5）中有5个物理量（R，λ，μ，D，t），令相似常数分别为cR，cμ，cλ，ct和cD，即

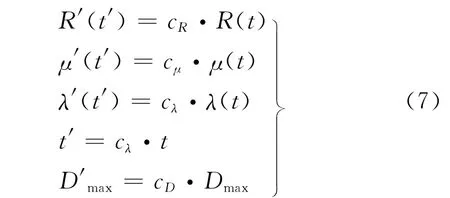
将式（7）代入式（6），有

考虑到式（5）中只有2个物理量纲（s和bit，即时间量纲和信息量纲［17］），则根据相似第二定理，可知其相似准则数应为：物理量个数－基本量纲个数＝3个.简单起见，要求相似现象中的可靠度R′（t′）与原始现象中的可靠度R（t）保持不变，即cR＝1；且取平均数据到达间隔时间和平均服务时间的相似常数相等，即cμ＝cλ；根据相似第一定理，联立式（5）和式（8），则可得cμ·cD＝1.

由此，整理出 M／M／1排队网络的3个相似准则为

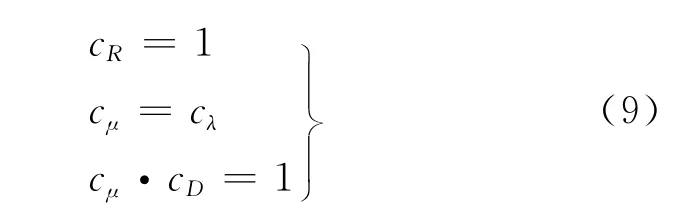
同时，要使两个现象相同，还需要满足相似第三定理，即要求单值量相似，也就是要求几何条件、介质条件、边界条件和起始条件.在本问题中，仅涉及起始条件，即要求两个现象t0时刻状态相同，而通常情况下，只要t0时刻起开始施加流量，即可保证t0时刻状态相同.

总结起来，根据相似理论三大定理可知，在如下情况下，基于M／M／1模型的网络排队及时可靠度等价：

1）网络平均服务时间和网络平均数据到达时间间隔同比例变化，即cμ＝cλ；

2）网络平均服务时间、平均数据到达时间间隔的变化与用户允许的最大时延的变化成反比，即cμ·cD＝1；

3）t0时刻起开始施加流量，即t0时刻状态相同.

随着网络数据到达强度的增加，相同时间内到达的数据包个数增多，可靠性信息量增大.为了达到可靠性试验截尾所需的数据量要求［18］，当网络数据到达强度增大ε倍以后，试验时长可减小ε倍，两次试验的数据量不变.即试验时长和网络数据到达强度的关系为

4 仿真验证

为了验证第3节提出的加速模型，根据网络数据到达强度是否变化设计了两类实验.

4.1 数据到达强度不变的情况

在该案例中，网络服务率为9 600bit／s，数据到达强度服从均值为1.0包／s的负指数分布，数据包大小服从均值为9 000bit的负指数分布，服务机制采用M／M／1的排队模型.

假定网络延迟故障服从二项分布［19］，取检验上限R＝0.999，鉴别比D＝1.50，生产方风险α和使用方风险β为10%，那么，可靠性鉴定试验中要求至少需要收集32 922个数据包的时延信息，因此至少需要仿真9.145h，才可到达此数量的数据包.应用OPNET仿真10h，总共收集到36 209个数据包，每个数据包的排队时延如图3所示.

取用户允许的最大时延要求Dmax＝60s，发现有969个数据包不符合要求，则可知网络不能满足R＝0.999的要求.

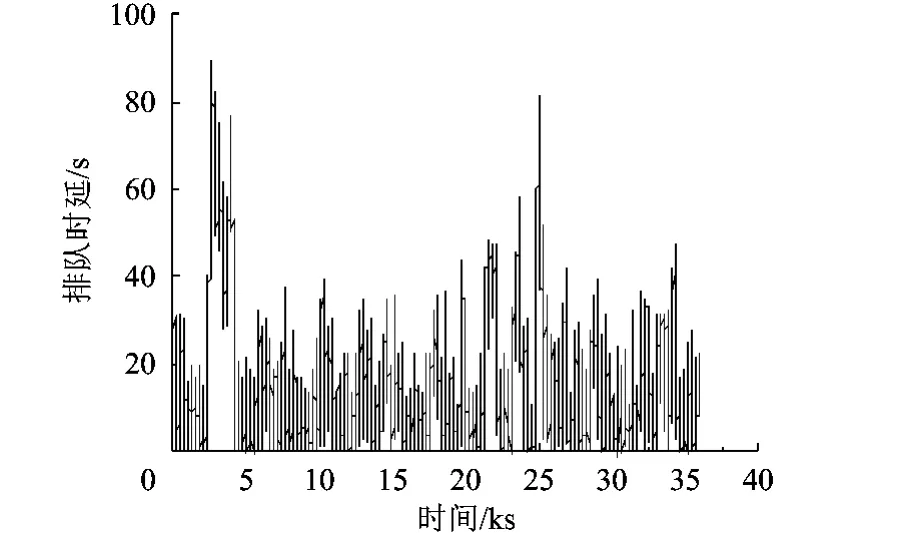
图3 原始网络每个数据包的排队时延

下面建立相似网络，根据第3节确定的加速模型，取cμ＝cλ＝4，cD＝ct＝0.25，t0时刻状态相同.如此，网络服务率为38 400bit／s，平均数据到达时间间隔服从均值为4.0包／s的负指数分布，数据包大小服从均值为9 000bit的负指数分布，服务机制仍采用M／M／1的排队模型.根据加速模型，仿真2.5h，共收集到36 180个数据包，每个数据包的排队时延如图4所示.由图可知，相似网络的排队时延与原始网络基本一致.

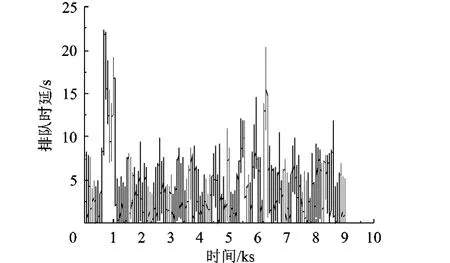
图4 相似网络每个数据包的排队时延

根据加速模型，取用户允许的最大时延要求Dmax＝15s，发现有969个数据包不符合要求，可知网络不能满足R＝0.999的要求，这一结论与原始网络相同.

随后，在原始网络和相似网络中分别以10min和2.5min为间隔，根据式（2）计算网络端到端及时可靠度的点估计值，两者的对比如图5所示，经计算其均方误差为0.012 06.

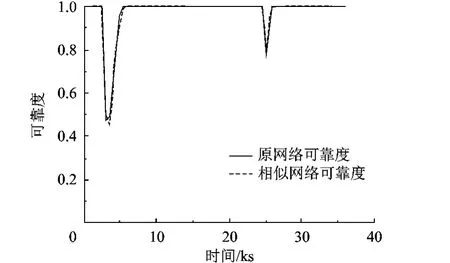
图5 原始网络和相似网络的及时可靠度对比

表1讨论了在不同的延迟故障判据下，原始网络和相似网络及时可靠度的均方误差.在本案例中，当原始网络时延阈值在30～60s变化时，两个网络及时可靠度的均方误差变化不大.由此可知，延迟故障判据的取值大小并不影响原始网络和相似网络在及时可靠度上的相似性.

表1 故障判据对加速模型的影响

表2进一步讨论了网络在不同的应力增加倍数下，原始网络和相似网络可靠度的均方误差.这里，当应力增加倍数在2～12倍变化时，两个网络及时可靠度的均方误差变化也不大.这说明，网络应力增加的倍数也不影响原始网络和相似网络在可靠度上的相似性.

在上述分析中，由于每个Δt时间段（原始网络中Δt＝10min，相似网络中Δt＝2.5min）只有约600个数据，故而两个网络的及时可靠性尚存在一定的误差.如果增加单位时间的数据量，则误差将大幅减小，如表3、表4所示，其绝对误差基本都在10－5附近.这也就是说，应用第3节提出的加速模型构建的相似网络，其及时可靠性与原始网络非常接近，且与延迟故障阈值、应力增大倍数的选取无关.

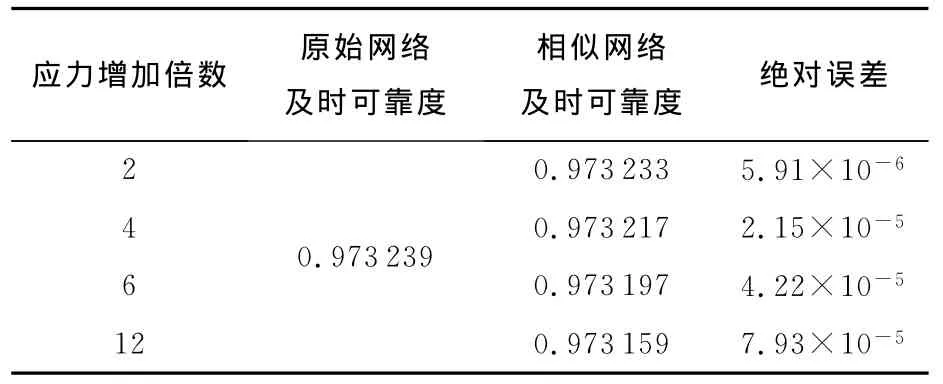
表4 应力增加倍数对加速模型的影响

4.2 数据到达强度变化的情况

网络运行过程中，数据到达强度随时间往往是变化的，这里再构造一个数据到达强度变化的案例.在该案例中，网络服务率为9 600bit／s，数据包大小服从均值为9 000bit的负指数分布，数据到达强度也服从负指数分布，其均值与时间的对应关系如图6所示（始终满足ρ＝λ／μ＜1）.服务机制采用M／M／1的排队模型.

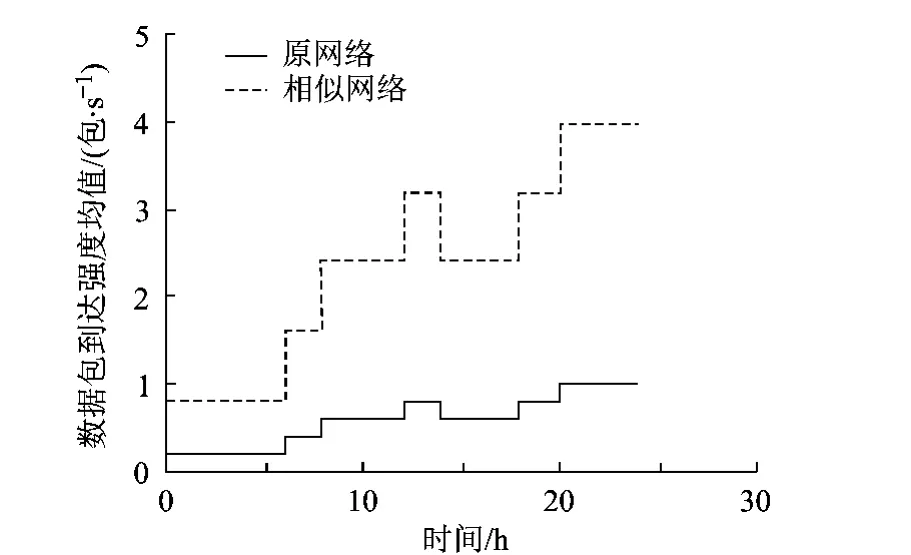
图6 数据到达强度随时间变化关系

根据第3节确定的加速模型，取cμ＝cλ＝4，cD＝ct＝0.25，t0时刻状态相同，建立相似网络.如此，网络服务率为38 400bit／s，数据到达强度均值与时间的对应关系变化如图6所示，排队模型中的其他信息不变.

应用OPNET在原始网络中仿真24h，得到50 612个数据包，在相似网络中仿真6h，得到50 611个数据包，两个网络中，每个数据包的排队时延分别如图7、图8所示，基本一致.

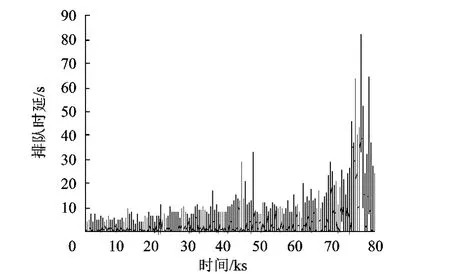
图7 原始网络每个数据包的排队时延

在原始网络和相似网络中分别以10min和2.5min为间隔，取用户允许的最大时延要求Dmax＝30s（相似网络中Dmax＝7.5s），根据式（2）计算网络端到端及时可靠度R（t）的点估计值，两者的对比如图9所示，经计算其均方误差为0.001 155.这说明，第3节的加速模型对数据到达强度变化的M／M／1排队网络仍然适用.

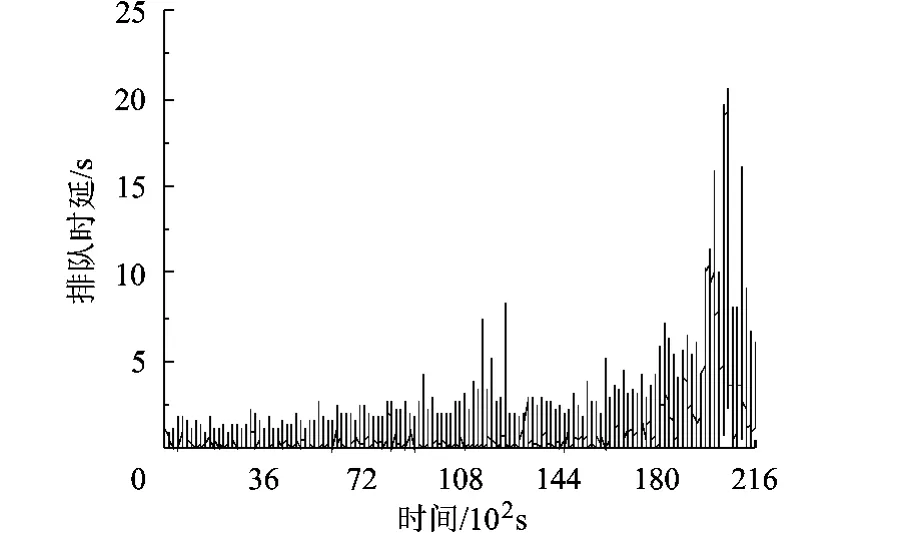
图8 相似网络每个数据包的排队时延

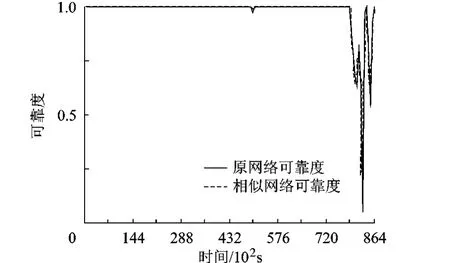
图9 原始网络和相似网络的可靠度对比

由此可知，对于服务机制采用M／M／1的排队模型的网络，在排队时延能达到稳定的情况下（即ρ＝λ／μ＜1），可以运用第3节的加速模型，设计加速试验方案，通过短时高应力条件下的网络及时可靠性反映正常应力下的及时可靠性.

5 结 论

本文分析了M／M／1排队网络的延迟故障机理，并根据相似三大定理，推导了端到端及时可靠性相似准则，得到了加速模型，并应用OPNET平台对该加速模型进行了验证.该加速模型适用于服务强度ρ＝λ／μ＜1的 M／M／1排队网络，通过增大数据到达强度，可有效缩短试验时间，解决网络可靠性试验时间长、成本高的问题.仿真结果表明相似误差小，且该加速模型的效用不随故障阈值、应力增加倍数变化，该加速模型为规划网络可靠性加速试验奠定了重要基础.接下来，需要进一步讨论其他排队模型下的网络可靠性加速模型，并进行试验验证.

（

）

［1］Duncan J Watts.The“new”science of networks［J］.Annual Review of Sociology，2004，30：243－270

［2］张建涛，张剑.军用通信网综合可靠性试验与检验［J］.电子产品可靠性与环境试验，2007，25（2）：19－22 Zhang Jiantao，Zhang Jian.Integrated reliability test and inspection for military communication network［J］.Electronic Product Reliability and Environmental Testing，2007，25（2）：19－22（in Chinese）

［3］Yurkowsky W，Schafer R E，Finkelstein J M.Accelerated testing technology［R］.RADC－TR－67－420，1967

［4］张春华，温熙森，陈循.加速寿命试验技术综述［J］.兵工学报，2004，25（4）：485－490 Zhang Chunhua，Wen Xisen，Chen Xun.A comprehensive review of accelerated life testing［J］.ACTA Armament Arii，2004，25（4）：485－490（in Chinese）

［5］Nelson W.Accelerated life testing－step stress models and data analysis［J］.IEEE Transactions on Reliability，1980，29（2）：103－108

［6］张志华.加速寿命试验及其统计分析［M］.北京：北京工业大学出版社，2002 Zhang Zhihua.Accelerated life testing and its statistics analysis［M］.Beijing：Press of Beijing University of Technology，2002（in Chinese）

［7］唐应辉，唐小我.排队论－基础与分析技术［M］.北京：科学出版社，2006：33 Tang Yinghui，Tang Xiaowo.Queuing theory－basics and analysis technology［M］.Beijing：Science Press，2006：33（in Chinese）

［8］朱信忠.网络分组交换中的排队论模型分析［J］.微机发展，2003，13：29－30 Zhu Xinzhong.Queuing theory model analysis of network packet switching［J］.Microcomputer Development，2003，13：29－30（in Chinese）

［9］何志鹏.基于排队论的Ad Hoc网络性能分析［D］.兰州：兰州理工大学电气工程与信息工程学院，2008 He Zhipeng.Network performance analysis for Ad Hoc based on queuing theory ［D］.Lanzhou：School of Electrical and Information Engineering，Lanzhou University of Technology，2008（in Chinese）

［10］徐挺.相似理论与模型试验［M］.北京：中国农业机械出版社，1982 Xu Ting.Similarity theory and model testing［M］.Beijing：Chinese Agriculture Machine Press，1982（in Chinese）

［11］金立兵，金伟良，王海龙，等.多重环境时间相似理论及其应用［J］.浙江大学学报：工学版，2010，44（4）：789－797 Jin Libing，Jin Weiliang，Wang Hailong，et al.Multi－environmental time similarity theory and its application ［J］.Journal of Zhejiang University：Engineering Science，2010，44（4）：789－797（in Chinese）

［12］张驰 李新东.相似理论中时间相似的达成与意义 ［J］.郑州铁路职业技术学院学报，2011，23（2）：15－17 Zhang Chi，Li Xindong.Time similarity and its significance in similarity theory［J］.Journal of Zhengzhou Railway Vocational ＆ Technical College，2011，23（2）：15－17（in Chinese）

［13］Li Ruiying，Kang Rui，Huang Ning，et al.A practical approach for network application reliability assessment［J］.Eesploatacja I Niezawodnosc－Maintenance and Reliability，2009，43（4）：17－27

［14］李硕，黄宁，李瑞莹，等.通信网络服务可靠性参数分析［J］.系统工程与电子技术，2012，34（9）：1946－1950 Li Shuo，Huang Ning，Li Ruiying，et al.Analysis for service reliability parameters of communication networks［J］.Systems Engineering and Electronics，2012，34（9）：1946－1950（in Chinese）

［15］裴昌幸.现代通信系统与网络测量［M］.北京：人民邮电出版社，2008：108－109 Pei Changxing.Modern communication system and network mesurement［M］.Beijing：Posts ＆ Telecom Press，2008：108－109（in Chinese）

［16］纪阳.通信网理论概要［M］.北京：北京邮电大学出版社，2008：109 Ji Yang.Communication network theory summary［M］.Beijing：Beijing University of Posts and Telecommunications Press，2008：109（in Chinese）

［17］邓宇，邓非，戴濒君，等.信息运动学与动力学－信息运动三定律［J］.职业与健康.2007，23（19）：1750－1752 Deng Yu，Deng Fei，Dai Pingjun，et al.Information kinematics and dynamics：three laws of information kinematic［J］.Occup Health，2007，23（19）：1750－1752（in Chinese）

［18］GJB 899A－2009可靠性鉴定和验收试验［S］GJB 899A－2009Reliability testing for qualification and production acceptance［S］（in Chinese）

［19］Li Meinan，Li Ruiying.The failure distribution for service layer of communication networks［C］／／The 2nd International Conference on Consumer Electronics，Communications and Networks.Three Gorges，China：IEEE，2012