面向下行多天线传输的能效最优上行训练

刘 鑫 韩圣千 徐志昆 杨晨阳

（北京航空航天大学 电子信息工程学院，北京100191）

为了满足人们日益增长的无线移动通信业务需求，未来的无线通信正朝着追求更高数据率的方向发展.然而，高数据率的通信系统往往会导致更大的能耗.从能源可持续利用、环境保护和蜂窝系统运营成本等多个方面考虑，能量高效的无线移动通信得到了越来越多的关注.

能量效率（EE，Energy Efficiency）是指单位能量所能够传输的比特数.当只考虑发射功耗时，文献［1］的研究结果表明EE在频谱效率（SE，Spectrum Efficiency）趋于零时达到最优.但是当进一步考虑电路功耗时，EE和SE的关系不再这样简单，会受到网络结构和传输方案等多方面的影响［2］.现有研究主要集中在器件层、链路层以及网络层等来提高系统的EE［3］，其中多输入多输出（MIMO，Multi－Input Multi－Output）传输技术及信令资源配置是链路层优化的问题之一.

在无线通信系统中，收发机需要利用信道信息进行数据解调和预处理.发送训练信号是收发机获取信道信息的主要途径，但是训练信号所占用的频谱开销以及功率消耗则会降低系统的SE和EE.文献［4－5］分别以最大化信道容量下界和最小化信道估计误差的克拉美罗界为准则，研究了训练信号的最优长度、位置和功率.文献［6］研究了开环MIMO系统中的最优下行训练信号长度，当系统对训练信号和数据进行最优功率分配时，最优的训练信号长度等于系统的发射天线数.针对闭环 MIMO系统，文献［7］提出了面向SE最优的训练信号和数据之间的资源分配方法.在现有文献中，针对训练信号长度的优化主要以SE最优为准则，然而面向SE最优的训练设计通常对于EE不再最优.目前，只有少量文献研究了以EE最优为准则的训练设计问题，例如，文献［8－9］分别考虑了单用户和多用户开环系统的训练设计问题.

在时分双工（TDD，Time Division Duplex）闭环多输入单输出（MISO，Multi－Input Single－Output）系统中，基站利用上行训练和信道互易性，获得下行信道信息做预编码.研究基于EE最优准则的训练长度设计.首先证明了系统EE和SE上界是上行训练长度的凹函数，并分析了两种准则下最优训练长度之间的关系、及它们对系统EE的影响.分析和仿真结果表明，高信噪比时，基于EE最优的设计将退化成基于SE最优的设计；在一般情况下，与最大化SE的设计相比，最大化EE要求系统配置更长的训练.

本文所采用的数学符号定义如下：黑斜体大、小写分别表示矩阵、行向量，I表示单位矩阵，表示向量的模和范数；上标表示对矩阵或向量进行共轭转置，⊗表示克罗内克积；E［·］表示期望运算，N表示非负整数集合.

1 系统模型

考虑一个TDD闭环MISO系统，N天线基站服务单天线用户.假设用户经历块衰落信道，信道信息在一个上下行帧内保持不变，但在不同帧之间相互独立.帧结构如图1所示，每个帧包含T个符号，其中有t个符号用于上行训练.

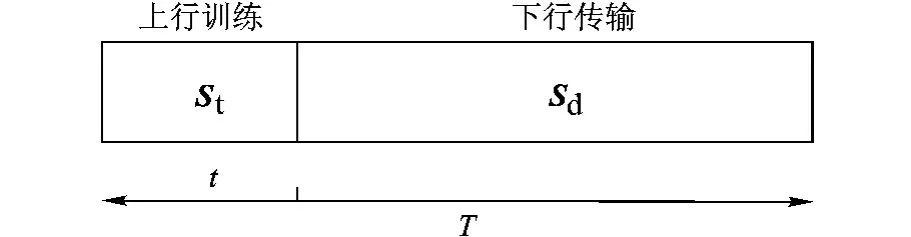
图1 TDD系统帧结构

令st表示上行训练信号，并满足stsHt＝Put，其中Pu为上行训练的发射功率，则基站接收到的训练信号可以表示为

采用最小均方误差（MMSE，Minimum Mean－Square Error）准则［10］，则基站可以得到上行信道估计值如下：

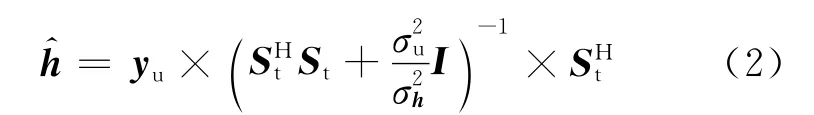
当采用MMSE估计时，估计信道与真实信道之间的关系可以表示为

基于TDD系统的信道互易性，基站可利用上行信道进行下行传输预编码，采用最大比发射（MRT，Maximum Ratio Transmission）传输［11］，预编码向量可以表示为

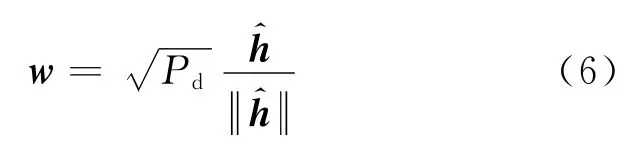
其中，Pd是下行数据发射功率.

用户的接收信号可以表示为

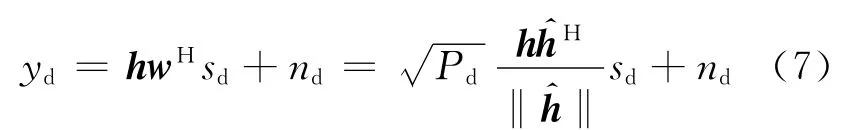
其中，sd为发送的数据信号；nd为均值为零方差为的加性白高斯噪声.

2 问题建模

2.1 净频谱效率

为了着重分析上行训练对系统性能的影响，假设用户能够获得理想的下行信道信息进行数据解调.由式（7）可以得到用户的接收信噪比为

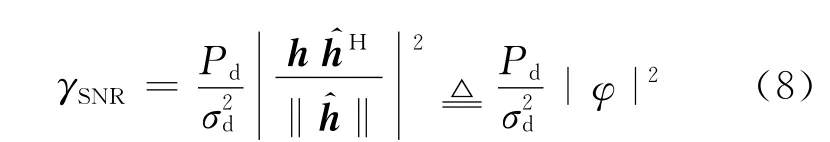
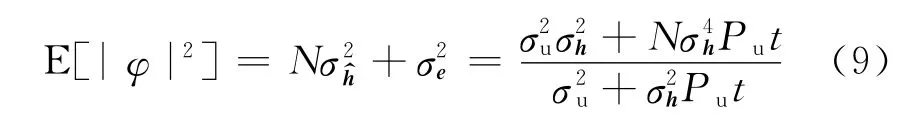
非理想信道下的各态历经容量可以表示为

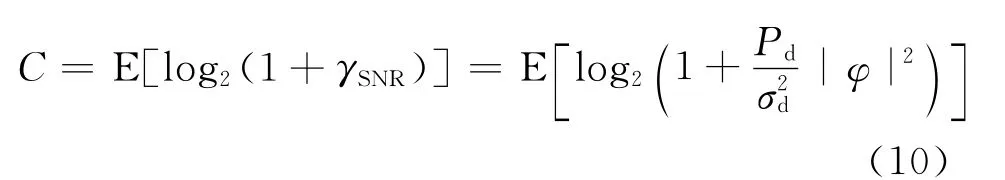
式（10）中的各态历经容量很难得到显示表达式，为了更容易地求解优化问题，利用詹森不等式，并代入式（9），可以得到各态历经容量的上界：

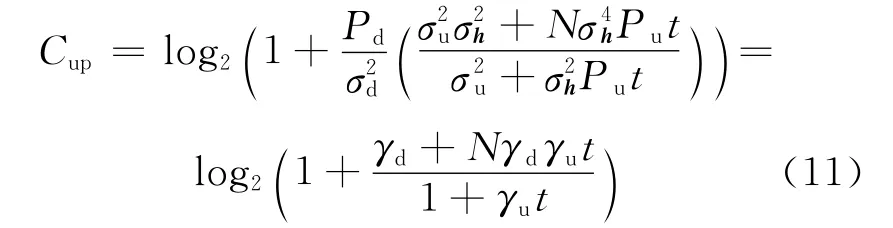
净频谱效率定义为

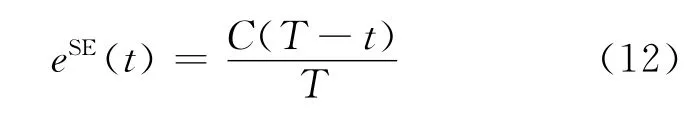
其上界可以表示为

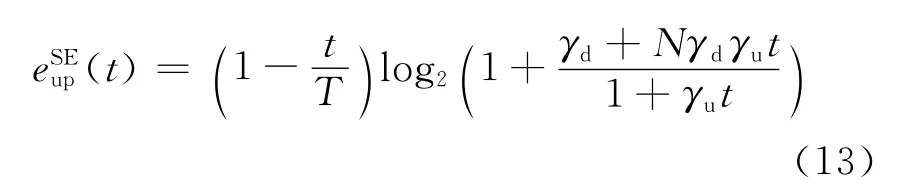
2.2 能量效率

用户端功耗远远小于基站功耗，为着重于系统整体能效设计，定义系统EE为净频谱效率与一个上下行帧内基站的总功耗之间的比值.

基站在上行训练阶段的总功耗只包括电路功耗，即

其中，PRXc为基站接收阶段的电路功耗，主要包括由射频链路、基带信号处理等引起的功耗.

在下行数据传输阶段，基站总功耗包括电路功耗和发射功耗.基于文献［12］给出的线性功耗模型，下行阶段基站总功耗Pbd可以表示为

其中，功耗参数μ反映了基站的功率放大器效率、制冷装置、供电等因素的影响；PTXc为基站发射阶段的电路功耗，主要包括由射频链路、基带信号处理等引起的功耗.

由式（14）和式（15）可以得到系统的总功耗：

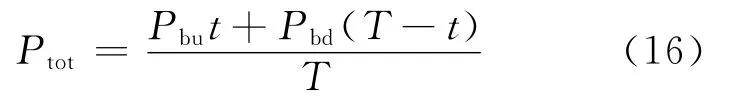
则由式（16）和式（12）可以得到能量效率为

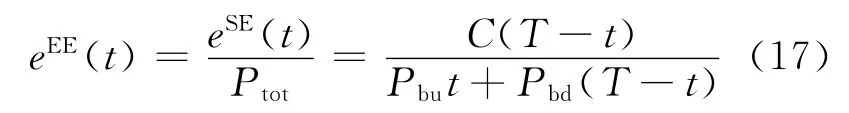
进一步考虑式（11），可以得到能效的上界：

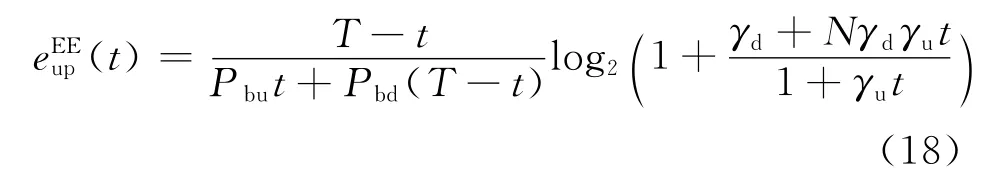
则以EE最优为准则的上行训练长度设计问题可以描述为

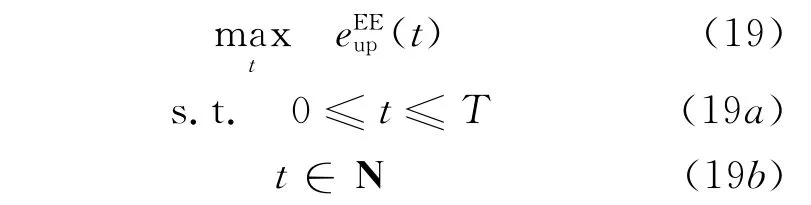
将在本文的第5节评估使用上界对训练优化带来的影响.

3 最优训练长度分析

3.1 最优训练长度

为求解优化问题（19），先将t松弛为［0，T］内的连续变量，再把最优解取整.下面证明松弛后的问题（19）是一个凸优化问题.

证明 为了简化符号，将能效上界式（18）表示为

不难得到其一阶、二阶导数分别为

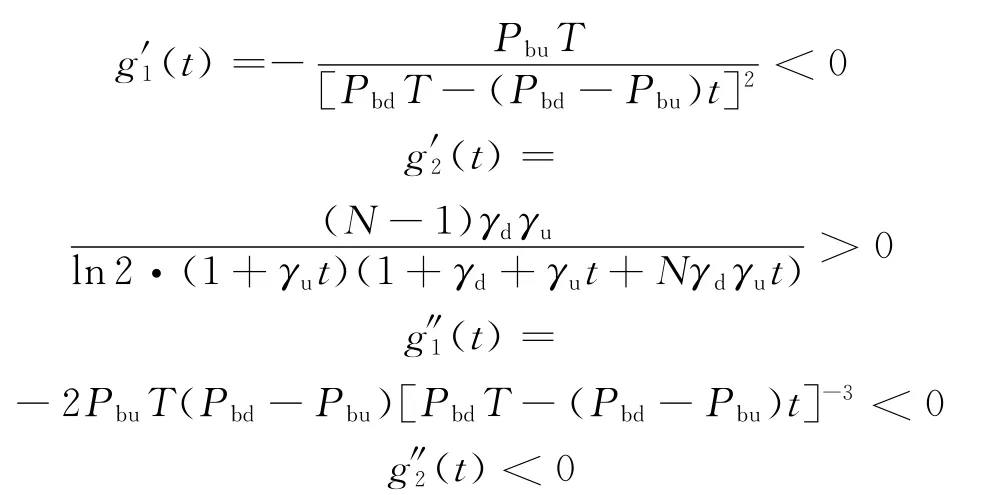
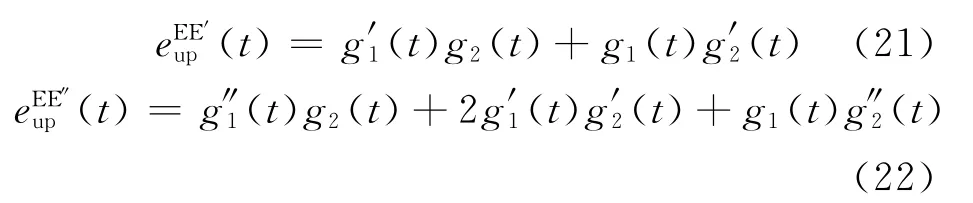
类似地，把谱效的上界（13）表示为

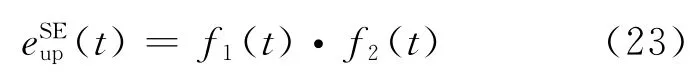
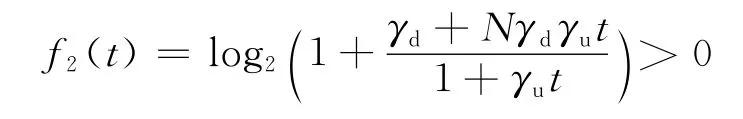
进而可以得到其一阶、二阶导数分别为

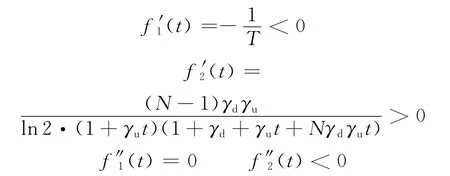
由此可以得到谱效的一、二阶导数如下：

3.2 两种准则下最优训练长度的差异

定义基于SE最优准则和基于EE最优准则下的最优训练长度分别为是优化问题（19）松弛后的最优解.由此，可定义两种准则下最优训练长度的差异为

命题2 Δt＊≥0恒成立.当时，当时，Δt＊＞0.

证明

令t＝0和t＝T，由式（21）、式（24）可以得到：

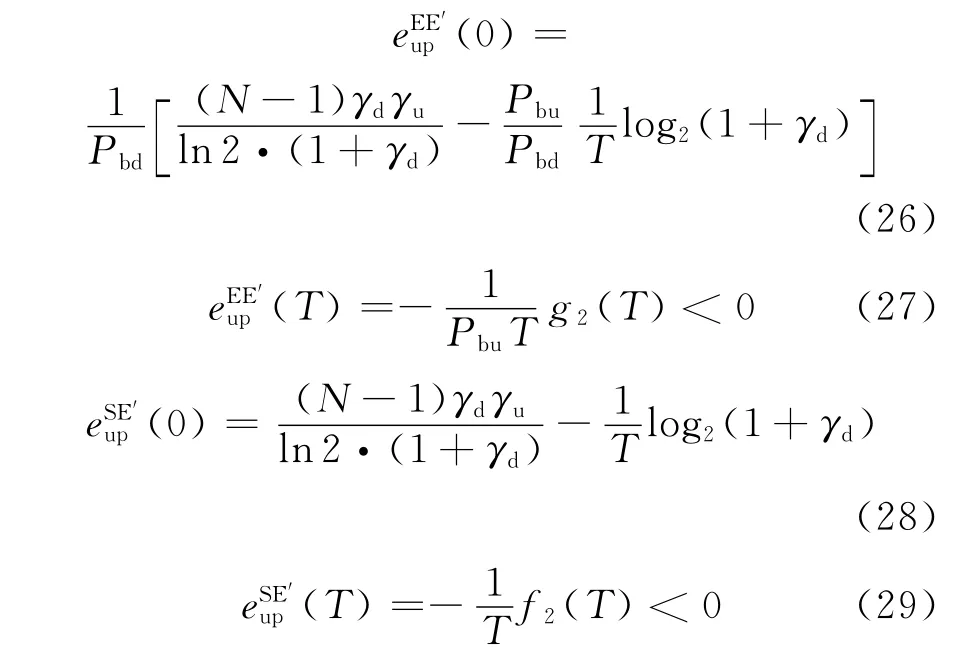
下面，分两种情况进行讨论.

这说明，此时能效最优和谱效最优的设计都不需要进行训练，Δt＊＝0.

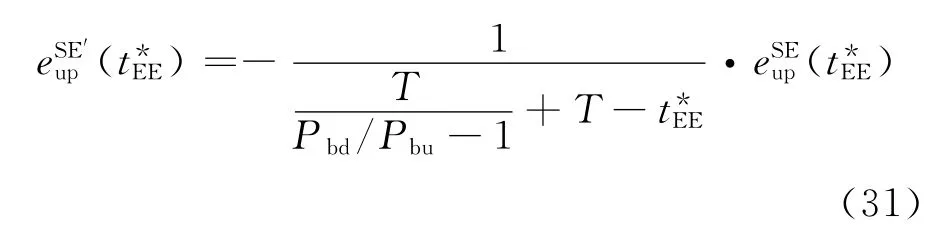
证毕

3.3 信噪比对最优训练长度差异的影响

因为上行训练的接收信噪比往往小于下行传输的接收信噪比，可将上下行信噪比之间的关系描述为由式（26）可见是信噪比的函数.为简化推导，用 G（γu）表示

其一阶导数为

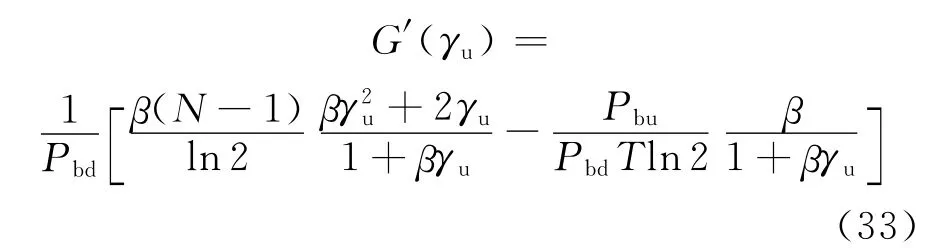
当γu→∞时下面分两种情况进行分析.

① 当t≥1时，由式（13）、式（18）可知，当γu趋 于 正 无 穷 时，趋 于趋于的渐进结果都是单调递减的，所以

3.4 电路功耗对最优训练长度差异的影响

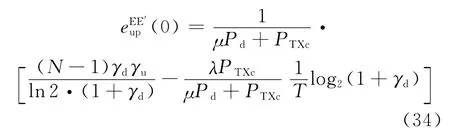
下面，分析基站发射阶段的电路功耗PTXc趋于零和趋于无穷大时的两种极限情况.

1）当PTXc→0时，趋于由命题2可知，此时先增后减

综上所述，当电路功耗足够小时，两种准则下的最优训练长度存在差异，Δt＊＞0；当电路功耗足够大时，是否存在差异取决于信噪比高低.

4 仿真结果

本节通过仿真评估最优上行训练长度对系统EE和SE的影响.如不做特别说明，仿真参数取值如表1所示.上下行发射功率、基站端电路功耗以及功耗参数取值来自文献［14］.

表1 仿真参数列表

为评估使用上界对训练长度优化的影响，分别给出利用式（11）信道容量上界和利用式（10）准确信道容量进行训练优化的结果.图2给出了两种情况下EE随上行信噪比的变化曲线.可以看到两种情况下的EE差别很小，这表明利用式（11）进行训练长度优化的有效性.

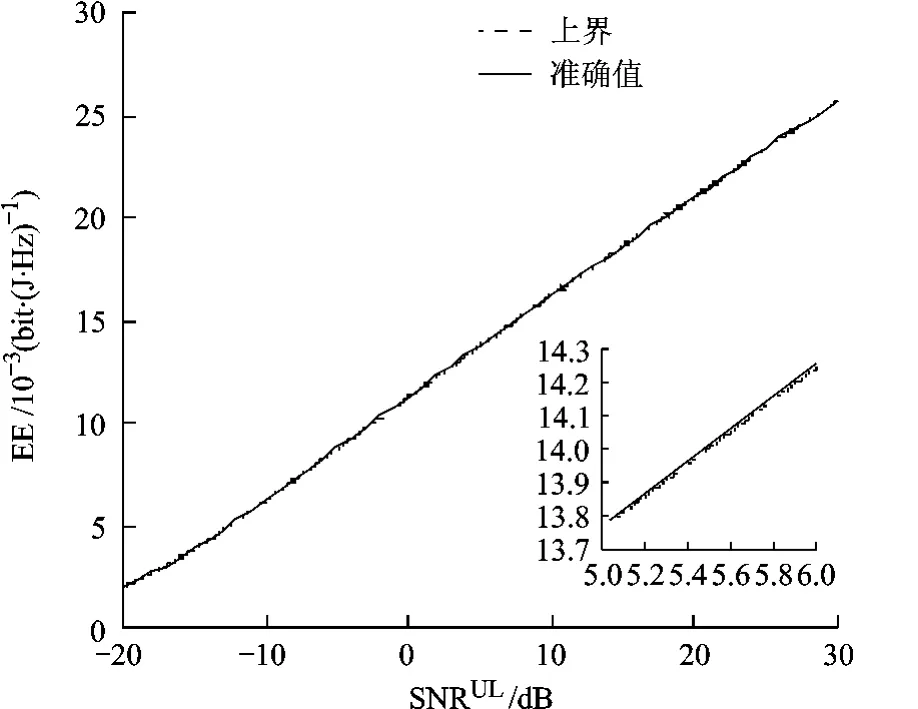
图2 能效随信噪比的变化曲线

图3给出了信噪比对最优训练长度的影响.如图所示，随着信噪比的增大，最优训练长度及差异逐渐减小.当上行信噪比γu取值较大、超过13dB时在一般情况下仿真结果与前面的分析一致.

最优训练长度差异Δt＊会受电路功耗的影响.如图4所示，当电路功耗很低时，两种准则下的最优训练长度存在明显差异；当PTXc逐渐增大时，最优训练长度是否有差异取决于信噪比.当给定信噪比时，最优训练长度差异Δt＊随着PTXc的增大而减小.仿真中，取接收和发送阶段的电路功耗之比λ为0.5，当λ取其他值时，可以得到类似的结果（由于篇幅限制没有给出）.

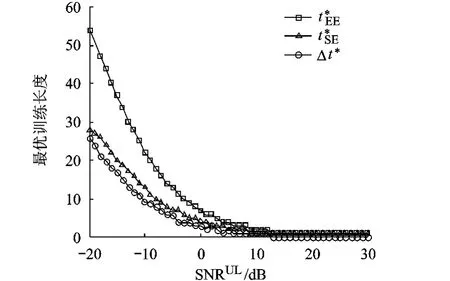
图3 最优训练长度随信噪比的变化曲线

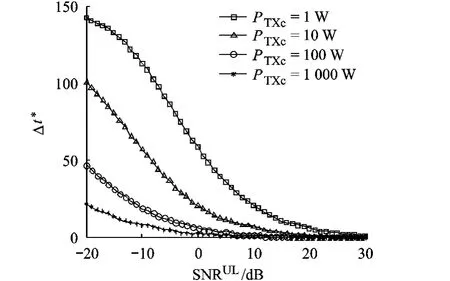
图4 最优训练长度差异受电路功耗的影响

图5给出了基于EE最优准则的设计相对于SE最优的设计所带来的EE增益和SE损失.用表示采用基于EE最优设计所达到的EE和SE；而用表示采用基于SE最优设计所达到的EE和SE.EE增益定义为，SE损失定义为如图5，随着信噪比的增大，EE增益和SE损失呈现减小的趋势，并随着电路功耗的增大而减小.这是因为最优训练长度差异伴随着信噪比和电路功耗的增大而减小.当信噪比足够高时，EE增益和SE损失接近于零，即EE最优设计将退化成SE最优设计.

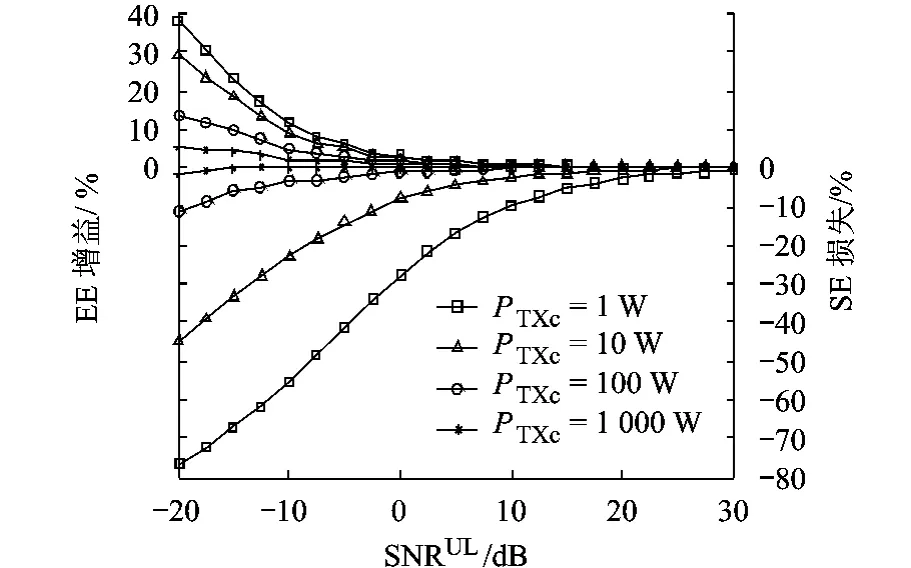
图5 EE增益和SE损失

5 结 束 语

本文研究了TDD闭环MISO系统中基于EE最优的上行训练长度设计问题.首先证明利用上界优化训练长度是凸优化问题；其次分析了基于SE最优和EE最优准则时最优训练长度之间的关系，指出了它们之间存在差异的条件.在此基础上分析了信噪比和电路功耗对最优训练长度的影响.理论分析和仿真结果表明，当信噪比很高时，基于EE最优与基于SE最优的训练设计结果相同；在一般情况下，与最大化SE的设计相比，最大化EE要求系统配置更长的训练信号.

（

）

［1］Verdu S.Spectral efficiency in the wideband regime［J］.IEEE Trans Inf Theory，2002，48（6）：1319－1343

［2］Li G，Xu Z，Xiong C.Energy－efficient wireless communications：tutorial，survey，and open issues［J］.IEEE Wireless Commun Mag，2011，18（6）：28－35

［3］Correia L，Zeller D，Blume O.Challenges and enabling technologies for energy aware mobile radio networks［J］.IEEE Commun Mag，2010，48（11）：66－72

［4］Adireddy S，Tong L，Viswanathan H.Optimal placement of training for frequency－selective block－fading channels［J］.IEEE Trans Inf Theory，2002，48（8）：2338－2353

［5］Dong M，Tong L.Optimal design and placement of pilot symbols for channel estimation［J］.IEEE Trans Signal Process，2002，50（12）：3055－3069

［6］Hassibi B，Hochwald B.How much training is needed in multiple－antenna wireless links［J］.IEEE Trans Inf Theory，2003，49（4）：951－963

［7］Kobayashi M，Jindal N，Caire G.Training and feedback optimization for multiuser MIMO downlink［J］.IEEE Trans Commun，2011，59（8）：2228－2240

［8］Gursoy M.On the capacity and energy efficiency of trainingbased transmissions over fading channels［J］.IEEE Trans Inf Theory，2009，55（10）：4543－4567

［9］Xu Z，Yang C，Li G.Energy－efficient power allocation between pilots and data symbols in downlink OFDMA systems［C］／／Proc IEEE Globecom.Houston，USA：IEEE，2011：1－6

［10］Scharf L.Statistical signal processing：detection，estimation，and time series analysis［M］.［S.l.］：Addison－Wesley Pub Co，1991

［11］Lo T.Maximum ratio transmission［J］.IEEE Trans Commun，1999，47（10）：1458－1461

［12］Fehske A，Marsch P，Fettweis G P.Bit per joule efficiency of cooperating base stations in cellular networks［C］／／Proc IEEE Globecom.Miami，USA：IEEE，2010

［13］Boyd S，Vandenberghe L.Convex optimization［M］.Cambridge，UK：Cambridge University Press，2004

［14］Auer G，Giannini V，Desset C.How much energy is needed to run a wireless network［J］.IEEE Wireless Commun Mag，2011，18（5）：40－49