综合评价脑循环功能的指标体系
,*,, ,
1. 复旦大学力学与工程科学系(上海,200433)2. 复旦大学生物力学研究所(上海,200430)3. 上海匡复医疗设备发展有限公司(上海,200433)4. 上海市东医院(上海,200438)
0 引言
脑血管疾病(如:卒中,脑出血等)是严重危害人类健康的三大疾病之一,具有发病率高、死亡率高、致残率高和复发率高的特点。大量动物与临床实验研究表明,如血管特性阻抗(Zc)、血管外周阻力(R)、动态阻力(DR)、血管顺应性(C)等脑循环动力学参数的异常,与脑卒中的发生与发展有着密切关系[1-10]。因此,检测脑循环动力学参数无论是对于脑血管疾病的早期诊断、脑血管疾病治疗措施和疗效的客观评价,还是对于脑循环的生理、病理学研究都有十分重要的意义。
随着血液动力学的发展以及新型无创检测技术的开发应用,目前已有几十个可以用于反映脑循环功能的动力学参数[1-11],而在诊断时往往还需要再加上各类临床诊断因素和血常规等,前后需要关注多达几十个参数,这让临床医生在解读数据时感到不便。因此,为了探讨通过脑循环动力学参数综合评价脑血管功能的方法,我们同时结合临床检测数据和部分血常规数据进行较为综合的建模,并得出能够反映脑循环总体功能的一个综合指标来便于医生判断及解读。为了验证模型的准确性和临床可读性,我们利用大样本临床病例数据对该综合指标进行了初步检验评价。
1 研究对象及方法
1.1 研究对象
800例,年龄25岁至70岁,平均年龄55.74±9.21岁,其中400例为脑血管病患者(如:卒中、脑出血等),均经CT或MRI确诊。400例为正常对照,要求为无糖尿病、高血压、心脑血管病史的健康者。
1.2 诊断定义及标准说明
脑卒中诊断按1986年全国第二次脑血管学术会议制定的中风诊断标准,并有头颅CT或核磁共振检查结果。各危险因素的暴露均有明确的定义和具体的判定标准:高血压病史为收缩压≥18.6kPa和舒张压≥12kPa,心脏病史包括先天性、高血压性、冠心病、心肌炎、心肌病和心律失常等。由患者本人提供,以县以上医院的诊断为准,糖尿病的诊断标准按照实用内科学第9版的标准。超重者为体重指数(BMI)≥24 E,脑卒中阳性家族史为一至三级亲属中有脑卒中病史者。
1.3 研究方法
采用上海匡复医疗设备发展有限公司研制生产的KF-3000脑循环分析仪(BCA)[16-18],分别通过连续波多普勒超声技术检测颅外流速,采用微型压力传感器检测颈动脉压力;脉冲超声波检测血管壁回波检测动脉血管管径;采用自动血压模块检测人体血压,经脑循环分析专用软件进行计算分析。获得反映脑循环功能状态的指标:
(1)运动学参数:平均、最大、最小脑血流速度(Vmean、Vmax、Vmin);平均、最大、最小脑血流量(Qmean、Qmax、Qmin)。
(2)动力学参数:①反映脑血管弹性指标的特性阻抗(Zc);②反映脑血管微循环通畅程度的外周阻力(Rc);③反映脑血管自身调节功能的动态阻力(Dr);④反映脑血管闭锁状态的参数临界压力(Pc)[1-12]。加上收缩压(Ps)与舒张压(Pd),共计12个指标。
1.4 统计学分析
建立数据库,用SPSS 10.0软件进行主成分分析、logistic回归分析[20,21],根据五种不同建模方法得出五个综合指标,利用ROC曲线对此五种计算方法所得指标进行评价,从而得出较优的一个方案。[24-25]
2 建模
2.1 年龄-体重-脑循环动力学指标第一主成分建模方案,得到综合指标1,记作M1
对400例样本数据的12个血液动力学指标和2个临床诊断指标(年龄,体重指数)进行主成分分析[22-24],确定主成分个数(累积贡献率达85%以上),并按贡献率大小对主成分进行排序。

表1 12个血液动力学指标及2个临床诊断指标各主成分的因子负荷量Tab.1 Principal component analysis of the 12 hydrodynamics parameters and 2 clinical diagnosis factors
由表1可见,前4个主成分的累积贡献率达到85.459%。其中第一主成分的贡献率为51.494%,各项变量的系数也与实际生理情况最为相符。根据主成分分析得出综合指标的常见方法,在此直接选取第一主成分得分作为综合指标1,记为M1。
2.2 年龄-体重-脑循环动力学指标主成分加权建模方案,得到综合指标2,记作M2
为了减少信息丢失量,在根据主成分分析得出综合指标中还有一种常见方法,就是将前几项主成分按照贡献率的大小进行加权得到综合指标。由表1可见,4个主成分的贡献率分别为51.494%、18.171%、9.810%、5.992%,综合指标=51.494%×第一主成分得分+18.171%×第2主成分得分+9.810%×第3主成分得分+5.992%%×第4主成分得分)/85.459%,记为M2。
2.3年龄-体重-脑循环动力学指标多元回归分析建模方案,得到综合指标3,记作M3
多元回归分析:以脑血管病的发病为应变量,以表1中的4个主成分作为自变量进行logistic回归分析[27],得到综合指标M3,见表2。根据表2的回归结果进行建模,可以看出第1主成分与脑血管病的发病相关度最高,而第2主成分与脑血管病的发病相关度极小。

表2 对前4个主成分进行logistic回归分析Tab.2 Logistic regression with front four principal components
2.4 血液动力学指标-临床诊断指标-血常规指标主成分加权建模方案,得到综合指标4,记作M4
对样本数据的12个血液动力学指标、7个临床诊断指标(年龄,体重指数,吸烟,饮酒习惯,脑中风史,心脏病史,高血压史)和血常规指标(甲状腺参数和血脂参数)进行主成分分析[22-24],并按贡献率大小对主成分进行排序。为了减少信息丢失量,将前几项主成分按照贡献率的大小进行加权得到综合指标,记为M4。

表3 12个血液动力学指标及7个临床诊断指标及血常规指标各主成分的因子负荷量Tab.3 Principal component analysis of the 12 hydrodynamics parameters,7 clinical diagnosis factors and CBC parameters

高血压史-0.21294-0.06613-0.30165-0.054780.1824320.014437-0.142880.382310.528908糖尿病史-0.33435-0.172570.0434620.1218130.042133-0.19110.4628940.001978-0.19026脑梗史-0.40538-0.28570.026990.048620.231319-0.063920.113182-0.02323-0.01052吸烟习惯-0.19479-0.15511-0.099280.0381060.0013510.5902260.186081-0.16593-0.27118饮酒习惯-0.18235-0.141690.0361160.040778-0.300640.3508920.013248-0.206540.080178收缩压-0.034360.6449750.134610.449823-0.01620.0216010.386919-0.05440.157977舒张压0.3813110.5815870.1607340.597540.0222210.0114360.053211-0.0381-0.04006胆固醇(CHOL)-0.50184-0.360370.562221-0.05539-0.10618-0.04806-0.06155-0.041830.181813甘油三酯(TRIG)-0.37046-0.289280.2478720.036284-0.269020.0213130.2537550.0833490.093081低密度脂蛋白(LD1)0.13076-0.043840.841679-0.1205-0.04009-0.06278-0.15796-0.079440.0944高密度脂蛋白(HDL)0.7844690.4162950.052998-0.064880.061821-0.04045-0.13769-0.0211-0.09257APOA0.4273950.3228860.1411620.0093760.063851-0.1332-0.297990.008415-0.15841APOB0.141198-0.005420.810459-0.13561-0.087340.032363-0.02479-0.196330.104243TPOA-0.1293-0.037210.292372-0.030480.4957330.4837160.0706580.227568-0.12404T3-0.011730.044670.202180.024986-0.22638-0.130590.1213580.612819-0.31392T4-0.26956-0.130630.1244950.0129190.23419-0.480850.1644250.220935-0.03869MTSH0.3372980.2045530.000658-0.01554-0.040410.062917-0.102340.2662520.428428TG-0.120470.0137180.25202-0.041480.6396120.3941660.1031580.2356040.05938FT30.0315430.0118660.091783-0.17243-0.405790.1338010.0131050.484612-0.27621FT40.0367060.0479470.126003-0.031780.423821-0.438450.060981-0.03377-0.08633平均流速(Vm)0.927026-0.230180.0127090.0213170.0250150.0041240.1726730.0090020.053401最大流速(Vs)0.68866-0.46065-0.030790.320720.0076710.0128510.197222-0.025090.142034最小流速(Vd)0.945981-0.019470.001667-0.13960.0085780.0107020.125131-0.001640.00174最大流量(Qs)0.791729-0.3648-0.022960.3010170.0125340.0063150.165505-0.013420.099865最小流量(Qd)0.950334-0.014020.002333-0.118130.0157150.0057640.1156380.002209-0.00847平均流量(Qm)0.949771-0.179940.0119670.0333460.028608-0.000520.1492950.0139040.028369特性阻抗(Zc)0.0132040.556501-0.00896-0.366560.080732-0.050320.310033-0.125870.057132外周阻力(Rc)-0.895230.2532870.0169530.0925520.0090740.017463-0.05634-0.02312-0.02226动态阻力(Dr)-0.437840.61682-0.00989-0.36989-0.062920.0260670.34089-0.086440.103817临界压力(Pc)-0.385010.0810260.1106660.8095190.057736-0.00737-0.272990.01916-0.09881累计贡献率29.50%48.10%54.71%60.70%65.31%69.71%73.48%77.15%80.33%
2.5 血液动力学指标-临床诊断指标-血常规指标多元回归分析建模方案,得到综合指标5,记作M5
多元回归分析:以脑血管病的发病为应变量,以表3中的九个主成分作为自变量进行logistic回归分析[27],得到综合指标M5,见表4。根据表4的回归结果进行建模。
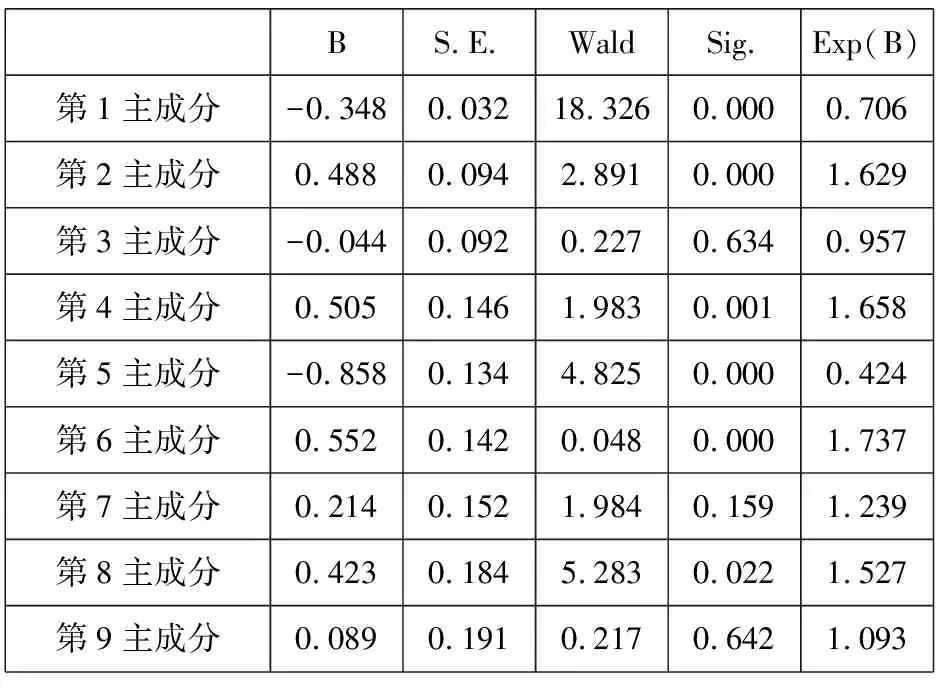
表4 对前九个主成分进行logistic回归分析Tab.4 Logistic regression with front nine principal components
3 检验分析
3.1 用原计算数据对4种模型进行检验分析
对原数据800例,年龄25岁至70岁,平均年龄55.74岁,其中400例为脑血管病患者(如:卒中、脑出血等)。400例正常人为无糖尿病、高血压、心脑血管病史的健康对照组。根据上述过程求得的综合指标值和实际发病情况,绘制ROC曲线图。ROC曲线下面积分别如表5所示:

表5 不同模型对应ROC曲线下面积Tab.5 The area under the ROC curve correspondin to different models
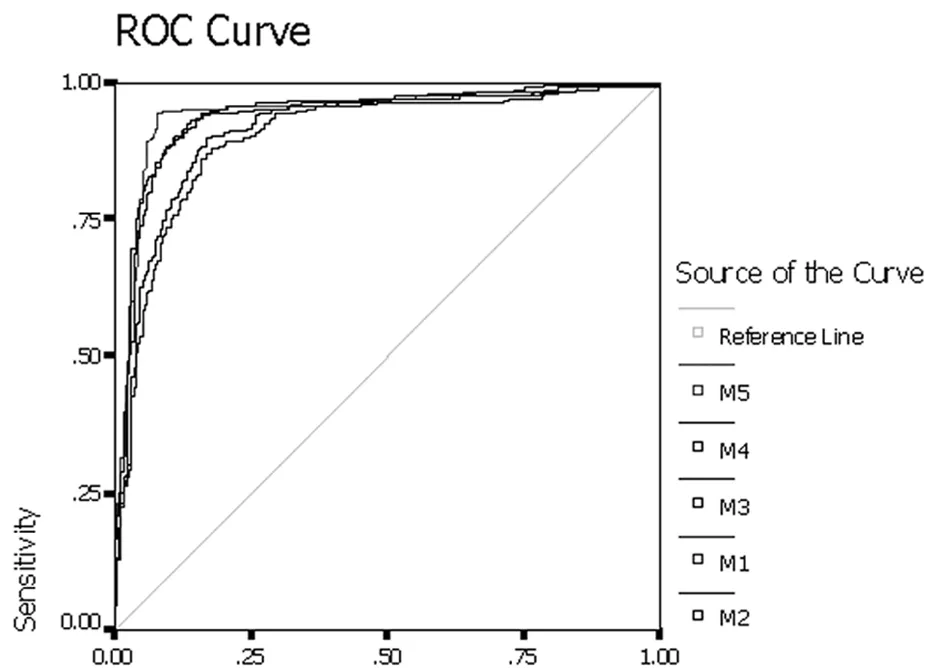
图1 800例人群患病概率与实际发病的ROC曲线Fig.1 ROC curve of 800 subjects probability of illness and actual incidence
从图1可以看出,5个综合指标的ROC曲线下面积均大于0.9,说明这5种建模方法在临床判定方面均较为准确,而使用了多元回归分析的M3和M5,ROC曲线下面积更是高达0.942和0.945,说明多元回归分析建模方法准确性更高。
3.2 另取人群进行临床应用检验分析
将5种计算模型应用到临床上的其他人群共计788例,年龄25岁至70岁,平均年龄51.34岁,其中368例为脑卒中患者。420例正常人为无糖尿病、高血压、心脑血管病史的健康者。利用上面得到的计算模型求出5个综合指标M1、M2、M3、M4、M5,根据综合指标值和实际发病情况,绘制ROC曲线图。ROC曲线下面积分别如表6所示:

表6 不同模型对应ROC曲线下面积Tab.6 The area under the ROC curve correspondin to different models

图2 788例人群患病概率与实际发病的ROC曲线Fig.2 ROC curve of 788 subjects probability of illness and actual incidence
ROC验证结果显示:5个综合指标的ROC曲线下面积均大于0.9,其中M4和M5分别高达0.957和0.961,与原始病历上反应出的结果一致,说明五种建模方式在区分正常人群和脑循环功能疾病患者方面都表现出了较好的性能。尤其是引入临床诊断指标和血常规指标的建模方式,得到的评价指标准确性更高。
3.3 对特殊年龄段人群检验分析
将5种计算模型应用到另一批数据680例,年龄为50岁至65岁,其中310例为脑血管病患者,370例正常人为无糖尿病、高血压、心脑血管病史的健康者。利用上面得到的计算公式求出五个综合指标M1、M2、M3、M4、M5,根据综合指标值和实际发病情况,绘制ROC曲线图。ROC曲线下面积分别如表7所示:

表7 不同模型对应ROC曲线下面积Tab.7 The area under the ROC curve corresponding to different models

图3 114例50岁至65岁人群患病概率与实际发病的ROC曲线Fig.3 ROC curve of 114 subjects aged 50-65 probability of iliness and actual incidence
根据临床数据表明,该年龄段是脑血管功能最易发生障碍的人群,而该年龄段的其他诊断干扰因素也最多。ROC曲线评价显示M1和M2的ROC曲线下面积均降低到0.9以下,但M3的ROC曲线下面积仍达到0.937,而M5模型因为引用更多临床参数而表现得更加准确,达到0.973。说明在干扰较多的情况下,多元回归模型所计算出的指标稳定性较高。
4 讨论
本研究通过结合脑血流动力学指标和临床诊断指标建立综合评价脑循环功能的模型,致力于得出便于临床医生解读和评价患者脑循环功能的综合评价指标。为了让指标具有更高的临床诊断价值和较高的稳定性,本研究在数据分析中引用了常用临床诊断因素和血脂及甲状腺功能参数。为了减少检测指标信息量的丢失,本研究选用了主成分分析和Logistic回归分析进行综合建模。
在选取建模变量时,模型M1,M2,M3分别使用的是脑血流动力学指标及年龄、体重指数,而模型M4和M5则引入了临床诊断时需要重点考虑的各种血脂、甲状腺功能指标和其他临床诊断指标。
在使用主成分分析进行建模时,本研究使用了二种方法:一是直接选用第1主成分(模型M1),二是根据各主成分的贡献率进行加权(模型M2)。而通过ROC曲线验证后发现模型M1的检验性能始终高于M2,可见直接选取第1主成分对比几个主成分加权的方法更能准确的综合反应脑循环功能。
在Logistic回归分析建模时,对自变量的选择目前尚无明确的规定,有研究仅选用对全部指标进行主成分分析后累积贡献率较高的前几项主成分为自变量[13],也有研究利用分析共线性,仅针对具有明显共线性的指标进行主成分分析,然后得到新的自变量。本研究根据前者得到评价模型,经ROC曲线验证,证明多元回归分析(主成分后logistic回归分析)具有更好的稳定性和评价效果。
本研究在建模后首先对原计算数据进行检验分析,5个综合指标的ROC曲线下面积均大于0.9,而使用了多元回归分析的M3和M5更是高达0.942和0.945。然后我们另外选取了一些样本(年龄25岁~70岁,788例)来评价模型在临床实际运用中的普适性,5个综合指标的ROC曲线下面积依然均大于0.9,其中M4和M5分别高达0.957和0.961,与原始病历上反应出的结果一致,说明各模型在区分正常人群和脑循环功能疾病患者方面都表现出了较好的性能,而引入更多临床诊断指标的M4和M5表现更为凸出。为了进一步验证模型的稳定性,我们选取了一组年龄在50岁-65岁的样本人群,根据临床数据表明,该年龄段是脑血管功能最易发生障碍的人群,而该年龄段的其他诊断干扰因素也最多,因此选择(50~65)岁人群进行检测具有特别的意义。ROC曲线评价显示M1和M2的ROC曲线下面积均降低到0.9以下,但采用多元回归分析法的M3与M5依旧表现稳定,M3的ROC曲线下面积达到0.937,而M5模型因为引用更多临床参数而表现得更加准确,达到0.973。
5 结论与展望
通过以上大样本ROC曲线检验评价可见,几种综合指标计算模型均能较好的反映脑循环的总体功能,可以对临床诊断起到一定的指导作用。而进行多元回归分析的M3和M5作为综合评定指标可能具有更好的稳定性和更高的检验价值。
在进一步研究中,我们还发现,不同的参数选取在针对不同患病人群进行检测时的表现各有优劣(例如加入血脂等血常规指标得出的参数对于区分脑梗病人和其他三高病人有更高的敏感性),这说明综合指标在实际应用中还可以进行针对不同病理的进一步细分。在接下来的研究中,我们希望能利用脑循环能量学参数将模型进一步优化,并从脑部供血状态、脑血管微循环状况、脑血管弹性等不同的方面制定更加具有针对性的指标,从而使研究结果更适合临床的推广应用。
[1] 丁光宏,王桂清,汪昕.脑循环动力学与脑血管疾病[J].中华神经精神科杂志,1995,28(脑血管疾病增刊):21
[2] 王盛章,姚伟,丁光宏.脑血流自动调节功能的三单元模型[J].医用生物力学,2007,22(3):268-272.[3] 龚剑秋,陆瑾,丁光宏,等.颈动脉血管壁切应力的分析[J].上海生物医学工程杂志,2004,25(4):10-14.
[4] Wei Yao, Guanghong Ding, A mathematical method to solve the inverse problem of a hemodynamics model. Recent Development in Theories & Numeric. [J]. World Scientific, 2002:403-410.
[5] Miroslaw Latka, Malgorzata Turalska, Marta Glaubic Latka, et al. Phase dynamics in cerebral autoregulation[J]. Am J Physiol Heart Circ Physiol,2004,289:2272-2279.
[6] Meng Law, Stanley Yang, James S. Babb,et al. Comparison of cerebral blood volume and vascular permeability from dynamic susceptibility contrast-enhanced perfusion MR imaging with glioma Grade, AJNR Am J Neuroradiol ,2004,25:746-755.
[7] 姚伟,丁光宏,吕传真.脑循环动力学参数识别与临床应用[J].中国生物医学工程学报,2003,20(2):120.
[8] 丁光宏、覃开荣、高建,等.脑循环血液动力学研究:Willis定常流力学模型[J].中国生物医学工程学报,1998,17(1):88-95.
[9] Ding Guanghong, Lu Chuanzhen, Yao Wei, et al.A hemodynamic model and a mathematical method to calculate the dynamics index for cerebral circulation[J]. of Hydrodynamics, Ser.B.9(4),71-81.
[10] 丁光宏,魏岗之.脑循环动力学模型与血管输入阻抗模拟[J]生物医学工程学杂志,1997, 14(1):4-10.
[11] 丁光宏,吕传真.脑循环脉动流的集中参数模型[J].力学学报,1996,28(3):336-346.
[12] 王京,史荫绵,李惜惜,等.脑血管疾病的超声及脑血管动力学指标检查[J].医用生物力学,1992,7(3):148-151.
[13] 曹奕丰,王桂清,黄久仪,等.脑血管血液动力学参数脑卒中预测模型的建立[J].中华流行病学杂志,2003,24(9):798-800.
[14] 王盛章,刘辉,丁光宏,等. 脑循环分析仪的研制[J].中国医疗器械杂志,2001,25(4):196-199.
[15] 刘辉,丁光宏,王盛章,等.脑WILLIS环循环分析专用软件研制:II临床应用[J].上海生物医学工程,2000,21(4):8-10.
[16] 刘辉,丁光宏,王盛章,等.脑WILLIS环循环分析专用软件研制:I软件功能介绍[J].上海生物医学工程,2000,21:(4)3-7
[17] 陆瑾.一种脑血管循环动力学检测分析仪器[P].中国专利:ZL200620047415.5,2006-11-01.
[18] 陈慎任.检测分析仪器(脑血管循环动力学)[P].中国专利:ZL200630043622.9,2006-11-01.
[19] 龚剑秋、李丽、丁光宏.脑循环功能检测技术近三十年进展[J].生物医学工程学进展, 2008,29(1):45.
[20] 张文彤,闫洁.SPSS统计分析基础教程[M].高等教育出版社,2004.
[21] 张文彤,董伟.SPSS统计分析高级教程[M].高等教育出版社,2004.
[22] Peter M. Okin, Richard B. Devereux, Richard R. Fabsitz, et al . Principal component analysis of the T wave and prediction of cardiovascular mortality in American Indians: The Strong Heart Study [J]. Circulation,2002,105:714-719.
[23] Anna Kiessling, Peter Henriksson.Perceived cognitive function is a major determinant of health related quality of life in a non-selected population of patients with coronary artery disease - a principal components analysis[J]. Quality of Life Research, 2004,13: 1621-1631.
[24] T. A. Hillier . A. Rousseau . C. Lange . et al. Practical way to assess metabolic syndrome using a continuous score obtained from principal components analysis[J]. Diabetologia, 2006, 49: 1528-1535.
[25] Patrick J. Heagerty, Yingye Zheng. Survival model predictive accuracy and ROC curves[J].Biometrics, 2005,61 (1) , 92-105.
[26] Yingye Zheng, Tianxi Cai, Ziding Feng. Application of the Time-Dependent ROC Curves for Prognostic Accuracy with Multiple Biomarkers[J]. Biometrics, 2005, 62(1): 279 - 287.
[27] Yokota T, Ishiyama S., Saito T,et al. Lymph node metastasis as a significant prognostic factor in gastric cancer: a multiple logistic regression analysis[J]. Scandinavian Journal of Gastroenterology,2004, 39:4, 380 - 384 .
[28] Howard Lee, Hui C. Kimko, Mark Rogge, et al, Population pharmacokinetic andpharmacodynamic modeling of etanercept using logistic regression analysis[J]. Clin Pharmacol Ther 2003,73:348-365.
[29] Donna Henderson,Christopher J. Williams, et al Forecasting late blight in potato crops of Southern Idaho using logistic regression analysis[J]. Plant disease, 2007, 91(8):951-956.

