一种新的变步长LMS自适应算法

杨飞飞，阴亚芳

(西安邮电大学电子工程学院，陕西西安 710121)

自适应滤波是现代信号处理的重要组成部分。20世纪60年代由Widrow和Hoff提出最小均方误差(Least Mean Square，LMS)算法。由于其结构简单、计算量小、易于实时处理，因此，在噪声对消、谱线增强、系统辨识等方面得到广泛应用［1］。

针对传统的LMS算法中收敛速度、时变系统的跟踪能力和稳态误差之间的矛盾［2］，人们作了各种改进［1－11］，提出了多种变步长LMS算法。变步长的自适应滤波算法的指导思想为［3］:在迭代初始阶段或未知系统参数发生变化时，应使用较大的步长，以加快收敛速度或提高对时变系统的跟踪能力;而在算法逐渐进入稳态时，无论主输入端有多大的干扰信号，都保持较小的步长以达到较小的稳态失调误差。文献［4］中提出的S函数变步长LMS算法，其步长μ是误差e(n)的Sigmoid函数，由于 Sigmoid函数过于复杂，且在e(n)接近于零处变化过大，不具有缓慢变化的特性，使得该算法在自适应稳态阶段仍有较大的步长变化，从而影响稳态误差［5］。文献［6］通过改进文献［4］的算法，提出了新的变步长自适应算法，该算法简单且在参数稳定后具有缓慢变化的特性，进一步减小了稳态误差。但是，该算法在提高收敛速度的性能上依然存在不足。

本文针对以上问题，在文献［7］的基础上提出了一种新的改进LMS算法，更好地解决了加快收敛速度和减小稳态误差之间的矛盾。

1 LMS改进算法的提出

1.1 LMS自适应滤波

自适应滤波的原理如图1所示。

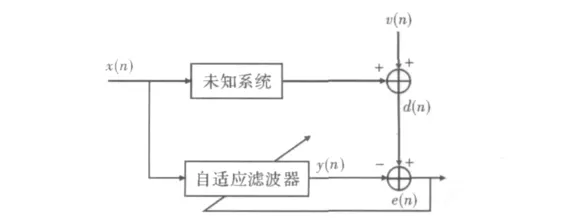
图1 自适应滤波器原理框图

基本的LMS算法的迭代公式为

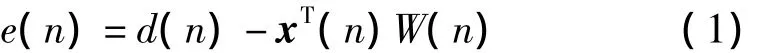
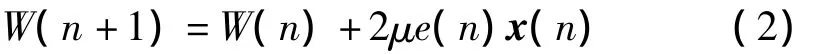
式(1)和式(2)中，x(n)为n时刻输入信号矢量;W(n)是n时刻自适应滤波器的系数;e(n)是误差信号;d(n)是期望信号;v(n)是测量噪声;μ是迭代步长。LMS算法的收敛条件是1＜μ＜λmax，其中，λmax是输入信号自相关矩阵的最大特征值。

1.2 改进的变步长LMS算法

文献［7］中的步长更新公式为

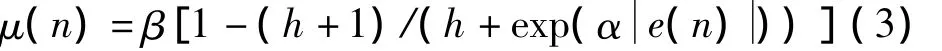
式中，μ(n)为步长;e(n)为误差信号，常数α控制双曲正切函数的形状，常数β控制函数的取值范围，常数h用来改善函数底部形状。

从上式可以得到

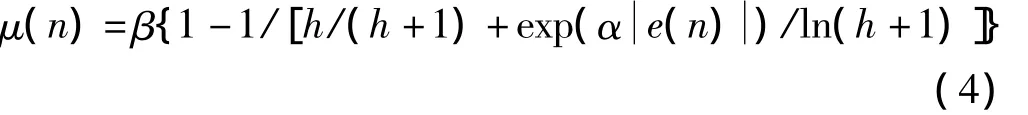
由文献［7］得出，h越大上式中μ(n)函数的底部越平缓，步长在误差接近零时具有更缓慢的变化趋势，在稳态时误差也更小。而当h过大时，(h/h+1)近似等于1。这里，假设γ=α/ln(h+1)，所以上述公式可以写做

由于LMS算法的收敛条件为［8］0＜μ(n)＜式中，R=E{x(n)xT(n)}，tr［R］为矩阵R的迹。因此，只要限制就能满足LMS算法收敛。

由变步长自适应算法的指导思想［3］，可以进一步改进算法，使得β正比于误差e(n，即e(n越大β越大越小β越小。这样，在迭代初始阶段较大，对应β较大，可得到较大步长μ(n)，从而获得较快收敛速度;当算法逐渐进入稳态时，逐渐地变小，对应β也随之变小，从而μ(n)更小，由此获得更小的超量均方误差。

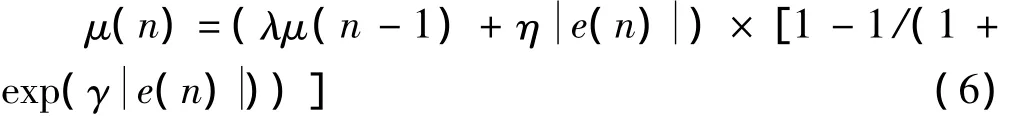
式中，参数λ是遗忘因子，且0＜λ＜1;参数η为＞0的常数。λ和η的值可依据实际情况来设定。参数γ用于改变双曲正切函数的形状。

这里增加以下约束，以满足算法收敛条件，

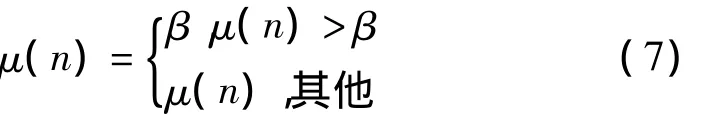
2 计算机仿真及分析

为说明新算法的收敛性能以及各参数对算法性能的影响，下面计算机仿真新算法应用于系统识别。

采用的仿真条件为:

(1)自适应FIR滤波器的阶数M=2。

(2)未知系统的FIR权系数为W*=［0.8，0.5］T。

(3)参考输入信号x(n)是零均值、方差为1的高斯白噪声。

(4)v(n)为与x(n)不相关的高斯白噪声，其均值为0，方差为0.04。

为得出每一条曲线，分别做1 000次独立的仿真，采样点数为500，再取统计平均，得到学习曲线。

图2为λ=0.01，η=0.99，γ=5时，不同β时的算法学习曲线，从上到下的3条曲线对应的β值依次为0.01，0.02，0.1。图3 为 γ =5，β=0.1，λ =0.01 时，不同η时的算法学习曲线。由图可知，随着β、η值的变大，算法的收敛速度逐渐提高。

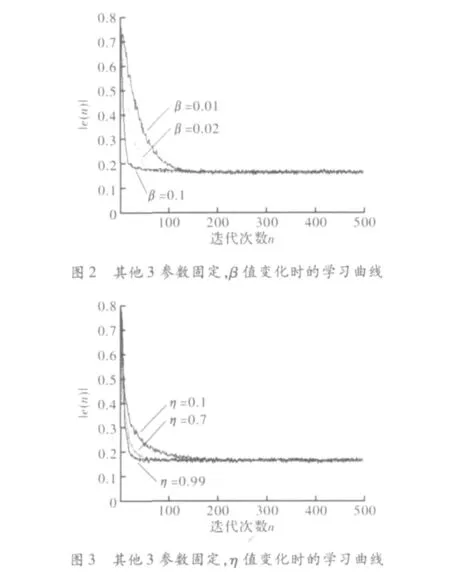
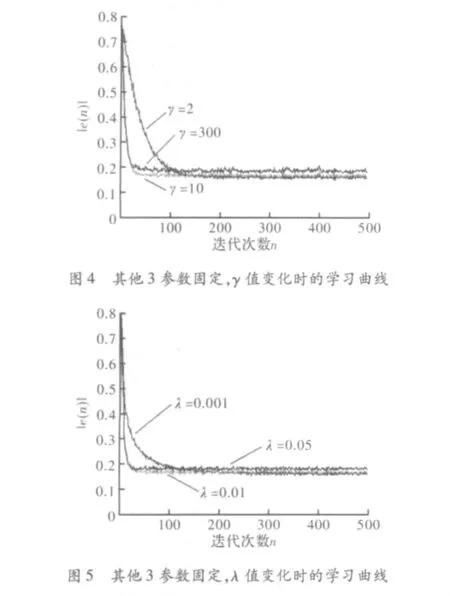
图4为β=0.1，λ =0.01，η=0.99时，γ分别为2，10，300时得出的3条学习曲线。图5为β=0.1，η=0.99，γ =5 时，λ 分别为0.001，0.01，0.05时的算法学习曲线。由图可知，随着γ、λ的增大，算法收敛速度提高的同时，超量均方误差也随着增大。

3 与其他算法的性能比较

下面通过计算机仿真实验对新算法和文献［4，6］提出的算法进行比较，以说明新算法的优越性。

仿真条件与上述实验条件(1)(4)相同，但在第250个采样点时刻未知系统发生时变，系统权系数变为 W*=［0.4，0.2］T。采样点数是 500，分别做 1 000次独立仿真，再取统计平均，得到算法学习曲线。

图6是新算法与文献［4，6］中的算法收敛速度的比较结果。其参数设定为 λ=0.98，η=0.12，β=0.06，γ=6。图7是新算法与文献［4，6］中的算法超量均方误差的比较结果。其参数设定为λ=0.86，η=0.06，β =0.23，γ =30。

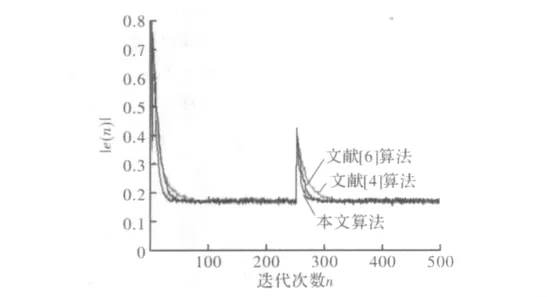
图6 与文献［4，6］算法收敛速度的比较

易得以下结论:在超量均方误差相同时，新算法比文献［4，6］算法的收敛速度更快，如图6所示;而在收敛速度相同的情况下，新算法比文献［4，6］算法的超量均方误差更小，如图7所示。

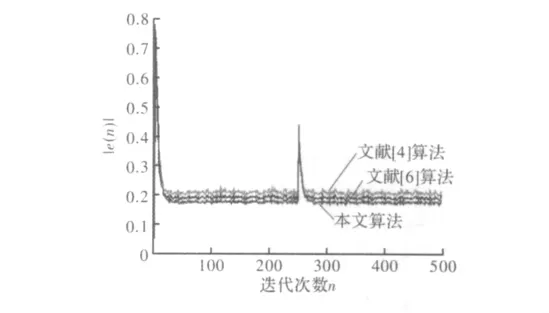
图7 与文献［4，6］算法超量均方误差的比较

4 结束语

本文是在文献［7］中提出的双曲正切函数改进形式的基础上提出的变步长改进算法，算法中β是时变的，是正比于误差信号e(n)的函数，这样在初始收敛阶段算法有较大的步长μ(n)及较快收敛速度;当算法逐渐进入稳定状态时μ(n)变小，由此得到更小的超量均方误差。此算法能更好地解决加快收敛速度和减小稳态误差的内在矛盾。仿真结果也表明，此算法性能优于文献［4］和文献［6］中的算法。

［1］刘杰.一种新的变步长 LMS自适应滤波算法仿真研究［J］.微计算机信息，2008，24(1－11):238－239.

［2］吕强，冯驰.一种变步长 LMS算法及其Matlab仿真［J］.应用科技，2006，33(6):80 －82.

［3］孙恩昌，李于衡，张冬英.自适应变步长LMS滤波算法及分析［J］.系统仿真学报，2007，19(14):3172 －3175.

［4］覃景繁，欧阳景正.一种新的变步长自适应滤波算法［J］.数据采集与处理，1977，12(3):171 －194.

［5］盛三元，王建华.一种新的变步长LMS自适应滤波算法［J］.华东船舶工业学院学报:自然科学版，2002，16(3):50－52.

［6］高鹰，谢胜利.一种变步长 LMS自适应滤波算法及分析［J］.电子学报，2001，29(8):1094 －1097.

［7］张中华，张端金.一种新的变步长LMS自适应滤波算法及性能分析［J］.系统工程与电子技术，2009，31(9):2238 －2241.

［8］FEUER A，WEINSTEIN E.Convergence analysis of LMSfilters with uncorrelated Gaussian data［J］.IEEE Transaction Acoustics，Speech，Signal Processing，1985(33):222 －229.

［9］张薇薇.一种改进的快速自适应滤波算法［J］.西安邮电学院学报，2011，16(3):6 －8.

［10］TANG J，ZHANG S J，WANG J.An improved variable step size LMS adaptive filtering algorithm and its analysis［C］.Guilin:Proc.of International Conference on Communication Technology，2006:1 －4.

［11］YAN Yonggang，ZHAO Junwei.An novel variable step size LMSadaptive filtering algorithm based on hyperbolic tangent function［C］.ICCASM，2010:233－236.