三相四线制电网谐波电流检测ip-iq法的改进

亓建英， 邹 黎， 李 超， 赵双东， 陈 群

(山东理工大学 电气与电子工程学院， 山东 淄博 255091)

有源滤波器中应用的基于瞬时无功功率理论的ip-iq谐波电流检测法已经在三相三线制电网中得到了广泛的应用[1]，但是运用在三相四线制电网中还存在一些问题：传统的ip-iq检测法为获得基波频率通过锁相环PLL产生与a相电压同相位的正、余弦信号[2]，而由于三相四线制电路中三相电压不对称，所以实际的正、余弦信号会有相、频差[3].文献[4]对该种情况下的锁相环进行了相应的改进，但改进后的电路设计较为繁琐，实际应用中不是最(佳选择．在三相四线制电路中，由于电路中零序电流的存在，使得Clarke变换不能直接应用，文献[5]中也提到了针对这一问题的改进，该方法是在Clarke变换得到α、β两相的基础上再加一个对应于零序的相,这种方法使得检测更加复杂．在谐波检测的过程中，滤波器的选用直接影响到谐波检测的精度．传统的谐波检测中选用低通滤波器LPF，一般采用Butterworth滤波器[6]，但是在滤除谐波时，需要滤除高次谐波，低通滤波器具有一定的延迟性且滤除不够精确[7]．

根据上述提出的问题，对ip-iq法在三相四线制电网中进行谐波检测时存在的问题做出三方面的改进：PLL环节的改进、电流正序分量算法的改进、LPF低通滤波的改进．

1 PLL环节的改进

在谐波电流检测中，PLL及正余弦发生电路得到的相位期望与a相电压的正序分量同相，频率期望为工频，而由于三相四线制电路中三相电压不对称，所以实际的正、余弦信号会有相位偏差和频率偏差，设该相位差为φ，经计算得相位偏差和频差不影响电流检测的准确性．以下给出计算过程：

首先，计算瞬时有功电流直流分量和瞬时无功电流直流分量为

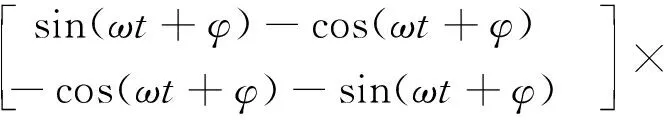
(1)

(2)

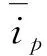
(3)

式中：iαf为α相基波电流；iβf为β相基波电流．

计算基波正序分量：

(4)

式中：iaf为a相基波正序分量；ibf为b相基波正序分量；icf为c相基波正序分量．

经计算，变换矩阵仅在变换过程中起作用，得到的基波正序分量与三相对称电路的正序分量相同，即电压不对称引起的正余弦信号的相位偏差以及变换矩阵与电网中电流存在的频差并不影响最终的检测结果.

除此之外，由于锁相环电路的设计较为繁琐[8]，且需要考虑产品成本的因素，而实际电力系统中经过补偿后期望得到50Hz的电流[9]，因此ω可直接设为314rad/s．

综上，谐波检测的过程中去掉传统方法中的PLL，只需设定固定角速度ω即可．

2 电流正序分量算法的改进

在三相四线制电路中，由于电路中零序电流的存在，使得Clarke变换不能直接应用．本文提出一个新的矩阵M用在Clarke变换之前，提前剔除零序电流带来的计算复杂性，再经过ip-iq法计算得到的正序电流分量即为谐波检测计算中需要用到的正序分量．下面给出新的方法中计算电流正序分量的具体计算过程：

(5)

(6)

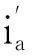
根据上述公式在进行Clarke变换之后，遵从传统的ip-iq法公式(1)～(4)继续计算，即可得到三相四线制中电流正序分量，这种方法将复杂问题简单化，且方便应用．

3 低通滤波器LPF部分的改进

陷波滤波器是一种特殊的带阻滤波器,其阻带在理想情况下只有一个频率点,它能在保证其他频率的信号不损失的情况下，有效的抑制输入信号中某一频率信息，因此也被称为点阻滤波器.这种滤波器主要用于消除某个特定频率的干扰，具有较高的精确度．针对低通滤波器LPF的延迟性和不精确性，基于改进中需要良好的选频特性和比较高的品质因数，本次设计采用的是电路比较简单，易于实现的双T型陷波器．

在我国采用的是50Hz频率的交流电，所以在平时需要对信号进行采集处理和分析时，常会存在50Hz的工频干扰[10]，对信号处理造成很大干扰，因此50Hz陷波器在日常生产生活中被广泛应用，其技术已基本成熟[11]．本文中关于滤波器的改进即是基于这种应用思想，将其反向应用，在滤掉工频后，再求差得到电流基波．

4 仿真分析

改进前后的原理图分别如图1、图2所示．

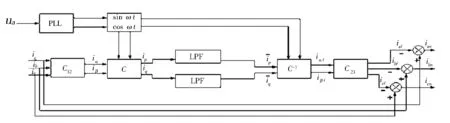
图1 传统ip-iq法谐波检测原理图

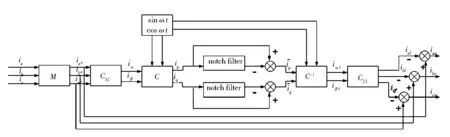
图2 改进后的谐波检测原理图

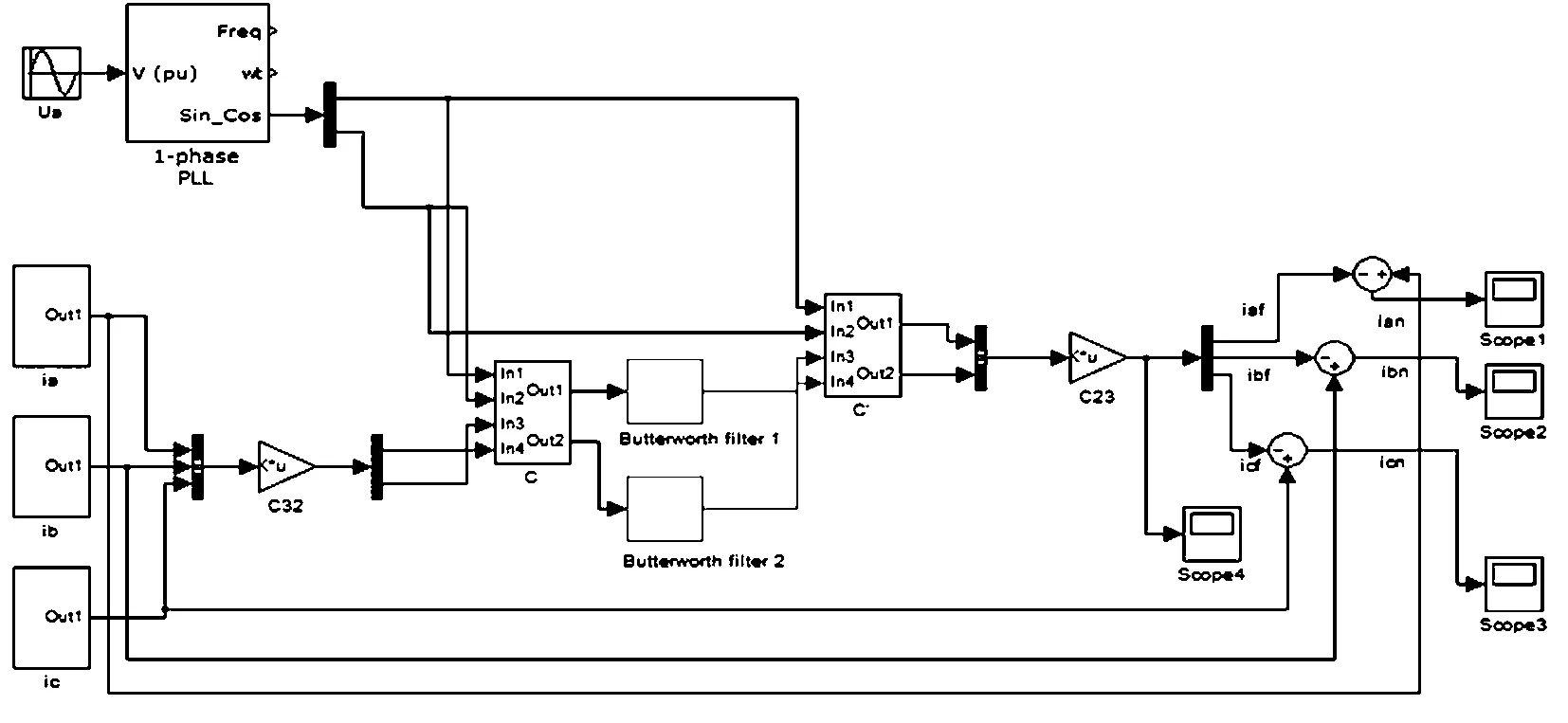
图3 传统的谐波电流检测模型

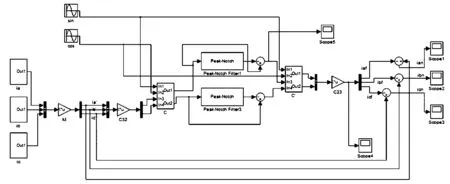
图4 改进后的谐波电流检测模型

在传统谐波检测原理的基础上，将锁相环PLL去掉，并在Clarke变换之前增加矩阵增益M，以去掉三相四线制中的电流零序分量，最后将低通滤波器PLF换成陷波器，并如图2所示进行连接．

4.1 仿真设置

根据以上分析在MATLAB仿真平台上分别搭建改进前如图3所示与改进后如图4所示的谐波电流检测的simulink仿真模型．模型中的三相电流由幅值220V的工频电流和小谐波电流(本仿真中取7次、13次、17次谐波)叠加而成；LPF选用二阶滤波、带宽为40Hz；为了取得更好的陷波作用，将notch-filter的陷波深度设置为40～50dB,中心频率设为50Hz，理论上双T型陷波器品质因数Q可调到50以上[12]，但是为了防止频率振荡，品质因数设置为50，将会取得较好效果．

4.2 仿真结果

根据前面所述进行设置，采用陷波滤波器的陷波效果：

如图5所示，当陷波器在频率为50Hz时,带宽窄、陷波深，具有精确的滤波效果．

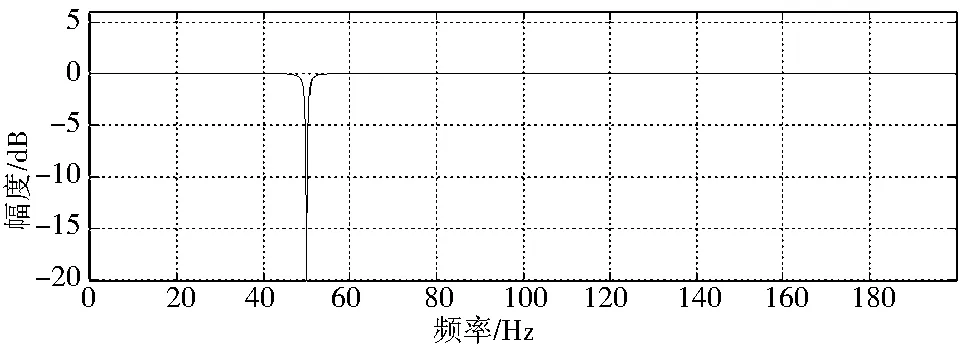
图5 陷波滤波器中心频率为50Hz时陷波

传统谐波检测得到的基波和谐波电流波形分别如图6、图7所示．

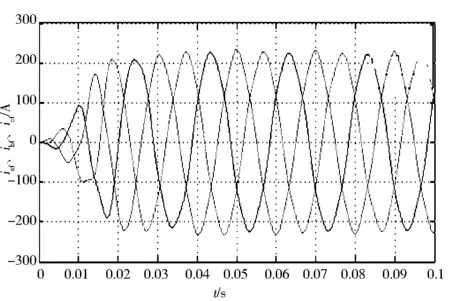
图6 传统ip-iq法中基波电流波形

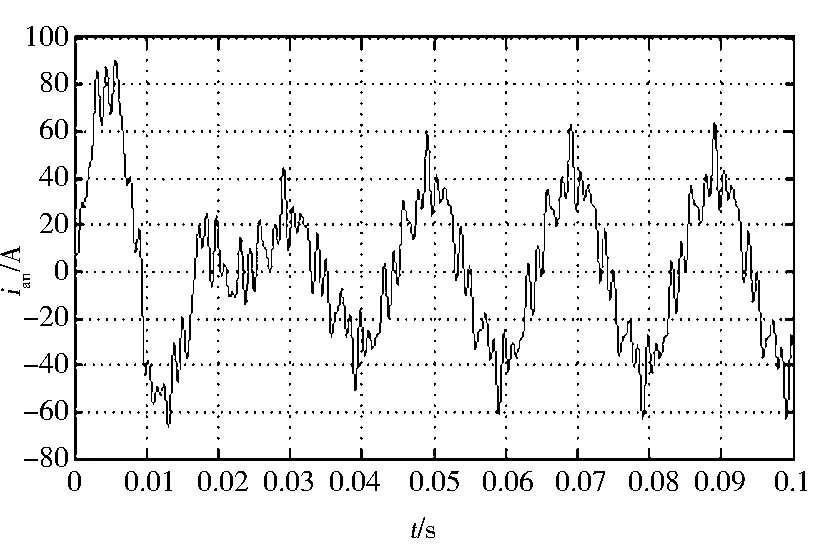
图7 传统ip-iq法中检测到的谐波电流波形

图6显示，传统ip-iq法对基波电流的跟踪存在延迟，该仿真中延迟时间约为0.01s,对谐波的检测不够准确，如图7所示，在0.01s之前检测到的谐波存在较大波动。

改进后谐波检测中得到的基波和谐波电流波形分别如图8、图9所示．

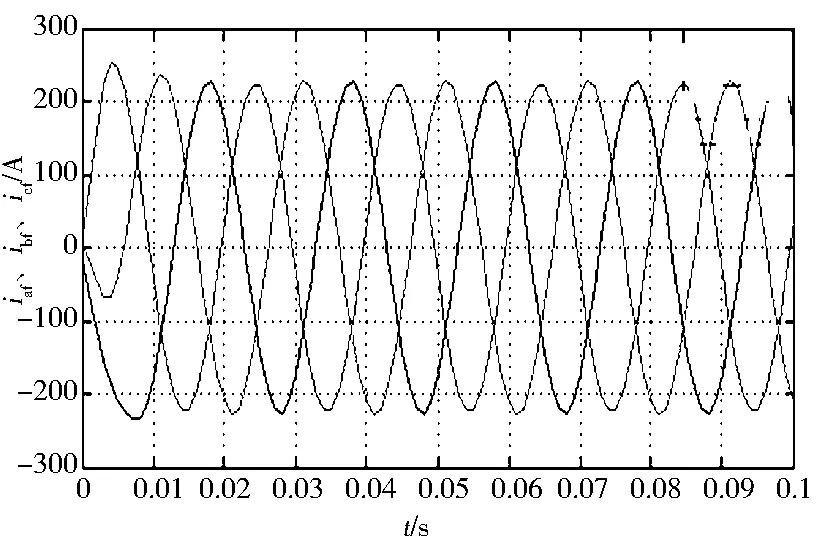
图8 改进后检测到的基波电流波形

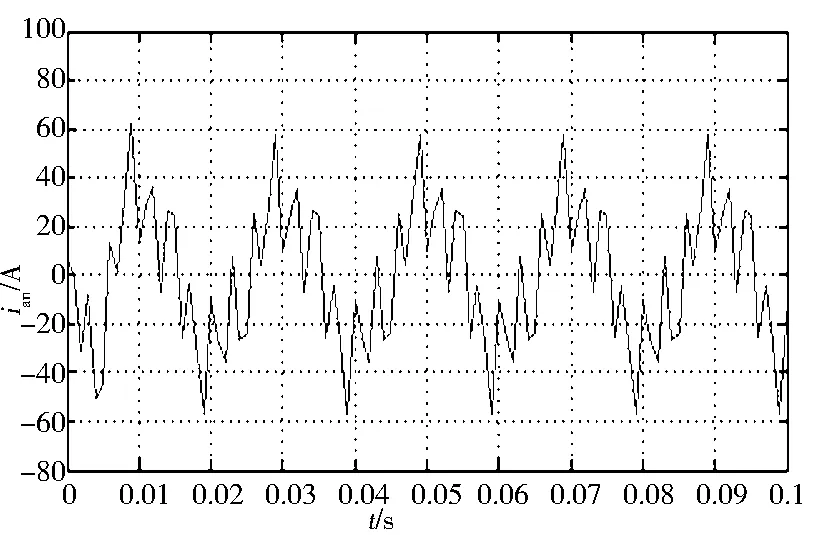
图9 改进后检测到的谐波电流波形

将图6和图8、图7和图9分别比较，得到的基波和谐波电流对比明显，传统检测方法中低通滤波器存在相对较大的延迟，不能及时跟踪基波、补偿谐波从而使得到的波形不够精确；检测方法改进后，响应速度快，几乎实现了瞬时跟踪，且谐波补偿接近理想状况，检测更为精确．

5 结束语

基于瞬时无功功率理论的基础，将传统三相四线制中谐波电流ip-iq检测法从锁相环、电流正序分量计算以及滤波器的重新选用这三方面进行改进并仿真，得到了较为理想的结果：去掉锁相环，直接构造正、余弦电路，缩小了整个检测电路，使得结构更为简单；构造矩阵去除三相四线制中的零序分量进而计算电流正序分量，使得所采用的算法不受三相四线制的约束；将低通滤波器改用陷波器,滤出50Hz电流后与含有谐波的原电流求差得到了更为精确的基波，使得整个谐波检测过程响应更快、更为准确．

[1] 王兆安, 杨军, 刘进军,等. 谐波抑制和无功功率补偿[M]. 2版. 北京: 机械工业出版社, 2009.

[2] Akagi H, Kanazawa Y, Nabae A. Generalized theory of the instantaneous reactive power in three-phase circuits[J]. IEEE & JIEE. Proceedings IPEC, 1983,103(4): 1375-1386.

[3] 王兆安, 李民, 卓放. 顺势无功功率理论和功率有源滤波器[C]//90年代电工科技进步学术年会论文集. 北京: 中国电工技术学会出版社，1991:10-12.

[4] 龚锦霞, 解大, 张延迟. 三相数字锁相环的原理及性能[J]. 电工技术学报, 2009,24(10): 94-99.

[5] Akagi H, Kanazawa Y, Nabae A. Instantaneous reactive power compensators comprising switching devices without energy storage components[J]. IEEE Trans Ind Appl, 1984, 20(3): 625-630.

[6] 曲学基, 曲敬铠, 于明扬. 电力电子滤波技术及其应用[M]. 北京: 电子工业出版社, 2008.

[7] 王秋生, 袁海文. 数字多频陷波滤波器改进设计方法[J]. 北京航空航天大学学报, 2011, 37(10): 1250-1255.

[8] 曾庆贵. 锁相环集成电路原理和应用[M]. 上海: 上海科学技术出版社, 2012.

[9] Kamichik S. 阻挡不需要频率的PLL滤波器[J]. 电子设计技术, 2011(3): 56.

[10] Li X Y, Rymer W Z, Li G L. The effects of notch filtering on electrically evoked myoelectric signals and associated motor unit index estimates[J]. Journal of Neuro Engineering and Rehabilitation, 2011(8): 64.

[11] Mao W L, Ma W J, Chien Y R. New Adaptive All-pass Based Notch Filter for Narrowband/FM Anti-jamming Receivers [J]. Circuits, Systems and Signal Processing, 2011, 30(3): 527-542．

[12] Chi B Y, Zhang C, Wang Z. A low noise amplifier with automatically Q-tuned notch filter[J]. Analog Integrated Circuits and Signal Processing, 2007,50(2):159-162．