应急项目中多组织协同治理策略研究

孙亚男，孙丽华

(1.山东财经大学工商管理学院，山东 济南 250014;2.山东财经大学 金融学院，山东济南 250014)

一、问题的提出

由于突发应急事件的发生对国家、社会和民众将产生重大影响，世界各国专家对应急项目管理从多个方面展开研究，取得了较丰富的成果。米特罗夫(Mitroff)、库姆斯(Coombs)等专家对危机管理主要影响变量和因素进行了研究，提出危机管理的四个主要变量包括:类型(Types)、体系(Systems)、阶段(Phases)和利益相关方(Stakeholders)［1］;以及四个基本因素包括:预防(Prevention)、准备(Preparation)、绩效(Performance)和学习(Learn)［2］。在此基础上，古斯(Guth)、希斯(Heath)、奥古斯丁等危机管理专家对危机管理生命周期阶段进行了梳理，提出了危机前(Precrisis)、危机(Crises)和危机后(Postcrisis)三阶段模型;减缓(Mitigation)、准备(Preparation)、反应(Response)和恢复(Recovery)的应急项目管理四阶段模型;和缩减(Reduction)、预备(Readiness)、反应(Response)、恢复(Recovery)和恢复力(Resilience)的SR模型、以及包括危机的避免、危机管理的准备、危机的确认、危机的控制、危机的解决和从危机中获利六阶段模型等一系列危机管理理论模型［3］。祁明亮等人在分析已有文献资料的基础上，指出当前对应急项目管理体系的研究主要从应急项目管理机理和机制两方面展开，并将公共事件分为自然灾害、事故灾难、公共卫生事件、社会安全事件等四类［4］。张江华则将已有相关研究概括为: 分级分类的研究主要集中在突发事件分级分类的事后评估、预案体系分级分类研究以及灾害风险评估三个方面，而对应急项目管理机制层面的研究主要针对应急项目管理体系中的机构设置以及法律、法规、标准的制定［5］。对应急项目管理决策的定量方法和模型的研究主要包括运筹学/管理科学的方法、基于博弈论的研究方法、复杂系统理论的研究方法以及基于模拟仿真的方法［6，7］。这些方法主要用于对资源管理问题、人员撤离问题、应急预案编制、应急处置中在线决策支持以及教育培训等内容进行分析研究［8，9］。

综上所述，当前针对应急项目管理的研究主要集中在应急项目管理理论模式、应急项目管理体系以及应急项目管理决策的定量方法与模型三个方面。但由于应急项目管理所面对的突发事件具有突发性、公共性、复杂性、破坏性、事先非可控性、变化发展的不确定性、处置的紧迫性以及影响的广泛性等特点，这就决定了应急项目管理必须具有临战统一决断性，与此同时，应急项目管理过程涉及多个组织和部门，各组织间的行为又相互影响，因此应急项目管理面临一个基本的冲突困境，即临战统一决断与多元组织间协同合作的脱节或者互斥。林凇等学者从组织内生性诉求出发，分析造成上述互斥的主要原因来源于内生性诉求缺乏满足的条件，即组织间缺乏清晰的权限和责任边界，缺少清晰的激励机制，以及缺失长效的合作伙伴关系和开放的信息平台等方面的问题［10］。张立荣等学者也指出“如何调动多元社会力量特别是企业组织、非政府组织以及公民个人的力量协同应对”将成为应急项目管理研究的重心［11］。为此，本文应用合作博弈理论对应急项目管理中多组织协同条件进行分析，提出合理的多组织协同策略，以保证应急项目管理中多组织间协同的高效性、稳定性和持续性。

二、问题描述

应急项目管理过程和组织具有临时性、动态性和一次性的特点，上述特点决定了应急项目管理需要在一个有限的时间范围内，采用临时性组织运行机制，通过有效的计划、组织、领导与控制，充分利用既定有限资源来完成一个既定的目标，因此，从应急项目角度分析，应急项目管理的核心是通过构建稳定的多组织协同关系满足应急项目管理过程的需求和达到既定的项目目标，上述协同关系的实现过程是一个对应急项目进行治理的过程，其本质属于项目治理研究范畴［12］。

应急项目管理过程作为一个项目治理过程，涉及多部门、多组织，并且各组织的行为相互影响和制约。政府作为应急项目管理过程中不可缺失的核心组织，通常利用其行政手段影响其他组织的行为，但仅依靠行政指令并不能保证多组织对应急项目的承诺，尤其是企业组织在整个应急项目管理过程中，将呈现出一种动态性，即各组织在参与应急项目的过程中，可能表现出积极参加、消极躲避或者威胁退出等行为。因为在社会责任体系不健全的环境下，参与应急项目的企业组织在考虑自身投资回报的时候，可能会将资源投入到其他有利可图的项目中，并利用各种借口逃避或者退出应急项目，以获得更高的收益，因此，政府各级部门在兼顾各参与组织的利益和总体效率的前提下，除了依靠行政指令之外，探寻更多的政策工具促进多组织协同完成应急项目将成为核心问题。上述协同的实现须包含两个方面的条件:一个条件是保证多组织优先选择应急项目;另一个条件是保证项目利益的合理分配。只有以上两个条件都得到满足，才能真正保证多组织对应急项目的承诺得以实现。

政府作为应急项目管理的核心组织仅依靠行政指令难以奏效，需要制定规范的决策机制促进多组织对应急项目的承诺。应急项目中的多个组织，特别是企业组织受到应急项目预算等资源的约束时，参与组织间将具有竞争行为。但应急项目管理过程中却需要各组织以应急项目的整体利益最大化为目标，来选择各自组织的行为，此时组织间的合作行为称之为协同。因此，本文运用合作博弈理论模型分析并建立规范的协同决策机制，促进多组织协同完成应急项目。基于合作博弈理论，本文提出如下前提假设:(1)参与应急项目的组织是个体或者群体理性的; ( 2) 参与应急项目的组织通过货币收益或者损失衡量各自的得失①企业收益不仅仅包括货币收益，也包括声誉、品牌、知识等无形资产收益，对应急项目而言，无形资产的收益更为重要。文中均采用货币价值对其计量。; ( 3)通过参与应急项目，各组织不会变得更差; ( 4)各参与组织博弈的最终目标是得到一个整体高效或者最优的结果，这个结果应促进多组织的协同。如果多组织将资源投入其他项目，或者通过非合作的形式可以获得更高的收益，则上述协同将变得不稳定。

基于以上的前提假设，运用合作博弈理论分析应急项目选择时，如果各组织没有预算的限制，非竞争的各组织往往乐于参与完成应急项目。如果各组织有预算的限制，特别是企业组织中股东利益受到损害的情况下，背离应急项目可能是最优策略，例如，各组织在应急项目中的既得利益不能满足组织的需求，或者参与应急项目的其他组织的预算与获利相比较少时，都可能出现上述情况。为此，本文将对以下问题进行分析和验证，即在没有预算限制的情况下，多组织协同完成应急项目是最优策略;在预算存在限制的情况下，当多组织协同完成应急项目作为最有效的实施形式时，可能对单个组织而言并非最优决策，在这种情况下，分析多组织协同策略同时满足个体和整体最优时的充分条件，因为参加应急项目是各级社会组织所必须承担的社会责任。

三、模型构建

(一)研究假设

在对问题描述的基础上，为合理构建分析模型，提出如下假设:

1.应急项目参与组织间不存在商业竞争。在这种情况下，单个组织从项目中获得收益数额简单相加即为应急项目中多组织协同的收益。由于不存在商业竞争，一个组织的收益增加并不会造成另外组织收益的减少。当然，即便存在商业竞争的组织间，如果应急项目仅从内部促使组织的运行效率提升，例如企业组织加班加点完成应急项目中的任务，而没有通过完成其他组织的项目任务获得利益，本文的结论也具有实用性。因此，应急项目的价值可以认为是单个组织所完成的项目价值的总和。

2.应急项目对每个组织的价值(value)是各组织潜在收益/损失分布的确定等值(CE，certainty equivalents)。因为在危机项目开支中，假设可以明确计算每个组织从每个项目中的获利是不现实的。因此，如果各组织的收益存在一个期望，U(value)表示项目价值的效用函数值，则U(value)=U(CE)，U(x)为效用函数。

3.多组织协同收益不少于项目的成本，否则组织不会选择参与完成应急项目。应急项目的估算成本是已知数，在此基础上将明确的应急项目的预算。

4.应急项目作为一个突发项目，是一个独立项目，因此不存在多应急项目间的协同作用。即多组织不会通过参与相关的项目而获得增效。参与应急项目的组织认为每个项目都是孤立的，确保组织完全参与到应急项目中。

(二)模型设计

基于以上研究假设，本文设定如下模型参数:

1.设N表示n个协同组织的有限集合，N={1，2，…，n};

2.设M表示m个备选项目的有限集合，M={1，2，…，m};

3.设Cj表示项目j的估算成本(或者预算支出)Cj，j∈M;

4.设组织 i从项目 j中得到的收益为 Bij，i∈N，j∈M;

5.设组织 i的预算为 Di，i∈N;

6.设组织 i承担项目 j的成本为 Sij，i∈N，j∈M;

解决前文提出的问题，即需要组织选择完成应急项目，同时还需要促使每个参与组织协同完成。因此，只有满足每个组织从应急项目中获取的收益比其他项目高，即决策目标需实现组织项目收益最大化，才能解决上述问题。为此，本文定义了一个混合整数线性规划模型，其中设Yj为(0－1)整数变量，作为选择最优项目的指示变量;同时设变量Sij作为组织所能承担项目费用的最优值。在此需要明确说明，变量Yj和Sij取值并非唯一。而每个组织所能承受的项目费不能超过其项目预算，同时参与协同的多个组织也不会接收净损失，以上将成为上述问题的核心约束条件。基于以上分析，混合整数线性规划算法1如下:

设共有S个组织参与应急项目中，S⊆N。

约束条件(1)表示组织的预算约束。约束条件(2)保证组织完全承担每个所选项目的费用。约束条件(3)表明各组织为理性组织，即组织的投入不会多于项目收益。在此需要说明，所选项目数以及各组织所要承担的项目费用额并不是唯一的，但是从组织协同整体而言，其净利润将会取得最大值。通过应用上述算法解决多组织选择项目的问题是“第一层最优结果”，而服从费用分配机制的约束条件时，将得到“第二层最优结果”。例如，可以设计一个让所有组织向某个特定项目中投入相同数额的预算，即采用均分策略，或者在一个受计划管制的环境中，合作成员可以依据计划规定的收益投入与之相“匹配”的预算。在这种情况，需明确一个约束条件，即组织投入应急项目的预算不会超过应急项目收益。同时也必须指出，某个应急项目的超额利润不会阻止理性组织的全面协同。依据总体效率性，包括上述约束条件的解，都将给出“第二层最优结果”。

在应用上述算法选择项目时，各组织的隐私信息值得关注。为了得到有效解，各组织在参加应急项目期间应完善信息披露机制。为保证理性组织披露信息的真实性，需要激励相容(incentive compatible)机制。Ferejohn等人研究表明，当组织仍然为每一个项目提供全部资助时，不存在同时保证有效性和激励相容的机制。Aloysius和Rosenthal进一步研究表明，不能通过任何激励兼容机制获得有效解。然而在完全信息情况下，他们提出了有效的费用分配机制，并说明了上述机制比实际中应用的一般方法更加有效;但是在信息保密和预算不做限制的情况下，虽然他们也提出了一个激励相容机制，但这种机制却无效［13］。需要指出，如果执行一个明确的费用分配机制，将因为其非线性整数约束，导致机制实现算法的计算困难。Han等人给出了一个算例，但是需要启发算法解决现实世界的规模问题［14］。

四、应急项目选择博弈分析

(一)没有预算约束的情况

定义1:任意非空的局中人集合N={1，2，3，…，n}的子集S⊆N，称之为联盟(Coalition)，所有联盟的全体记为P(N)。

定义2: n 人合作博弈( n≥3) 的特征函数是指定义在P( N) 上的一个实值有界函数v( S)，其中v( S)表示联盟S通过协调其所包含局中人的策略所能保证得到的可转让效用的总量。

一个特征函数也可被称为一个联盟型博弈(game in coalitional form)或一个联盟博弈(coalitional game)，简记为v(S)或v。

定义3:核心(core)是满足以下条件的支付向量X=(x1，x2，…，xn)的集合:

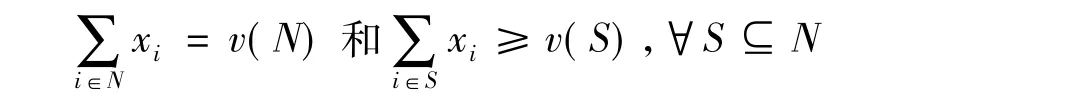
如果博弈的核心非空，就可以将协同总效用v(N)按照这样一种方式分配给各个局中人，使之不仅满足个体理性条件和集体理性条件，而且满足联盟合理性条件。但是，非空的核心并不能保证一个核心分配(core allocation)，原因在于博弈解是由合伙执行的费用分配组合所决定的。

定义4:博弈(N，v)具有超可加性，如果满足:v(S∪T)≥v(S)+v(T)，则∀S，T⊆N，S∩T=Ø。

定义5:博弈(N，v)是一个凸对策，如果满足:v(S)+v(T)≤v(S∪T)+v(S∩T)，则所有的S，T⊆N。

上述条件也可以记为:

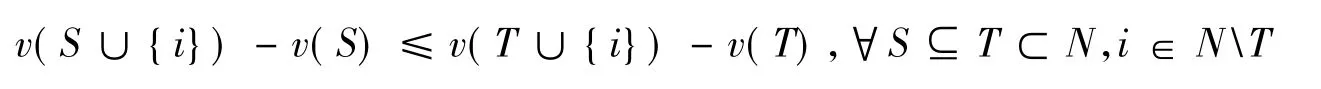
由上式可知，参加联盟的“诱因”将随着联盟成员数的增加而增大，因此当博弈合作时，将具有“滚雪球”或者“从众”效应。Shapley(1971)证明凸策略的核心总是非空［15］。

基于以上定义，本文提出命题1:

命题1:没有预算约束情况下，博弈G={N，v}的特征函数v(S)由算法1中目标函数所定义，则博弈具有非空核心。

证明如下:

如果没有预算的限制，同时联盟从S项目j获得的总收益远大于项目的投入，则联盟S将承担项目j的费用。如果组织集合T不承担项目的费用，则联盟S⊆T也不会承担项目费用。

由命题1对特征函数v(·)的定义可得:

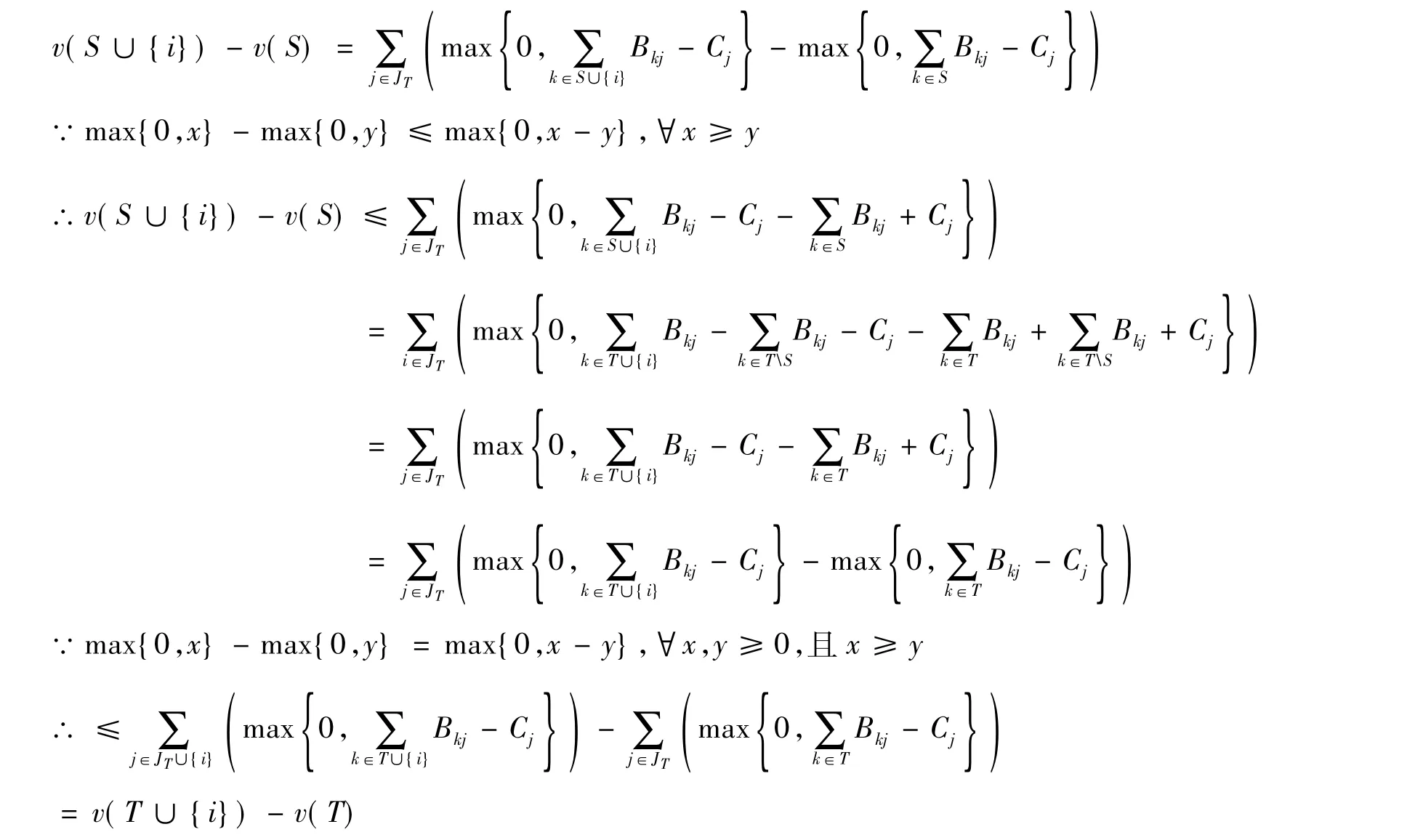
由定义5 可知，G = { N，v} 是一个凸对策，则凸对策核心非空。

命题1揭示出如果组织之间不存在竞争，同时不受到项目预算的约束时，各组织不能通过离开合作联盟而获利，因此，在这种情况下，多组织合作完成应急项目是一个最有策略，只要合作的组织间使用成本分担机制则必然有一个核心分配(core allocation)。

(二)存在预算约束的情况

当多组织对于应急项目有预算约束时，此外联盟S的值由算法1求得，本文提出命题2。

命题2:有预算约束的情况下，项目选择博弈的特征函数由算法1所定义，则博弈可能存在空核心。

证明如下:

有3个组织可参加包括应急项目在内的3个项目，分别记为组织1、组织2、组织3和项目1、项目2、项目3。具体参数如表1所示，不同联盟的净值如表2所示。

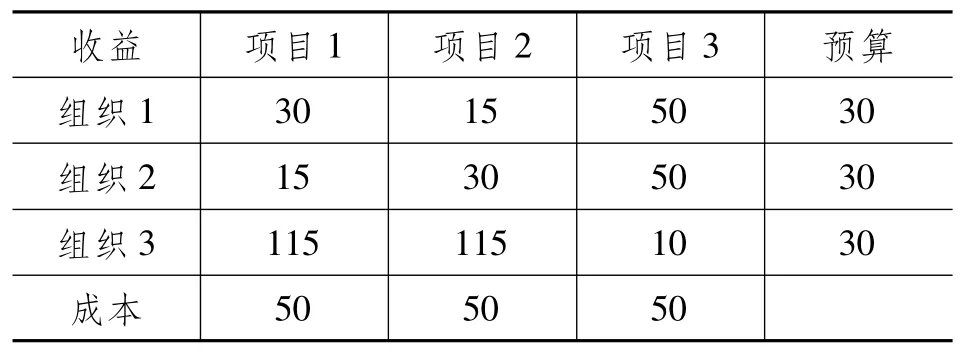
表1 案例相关参数

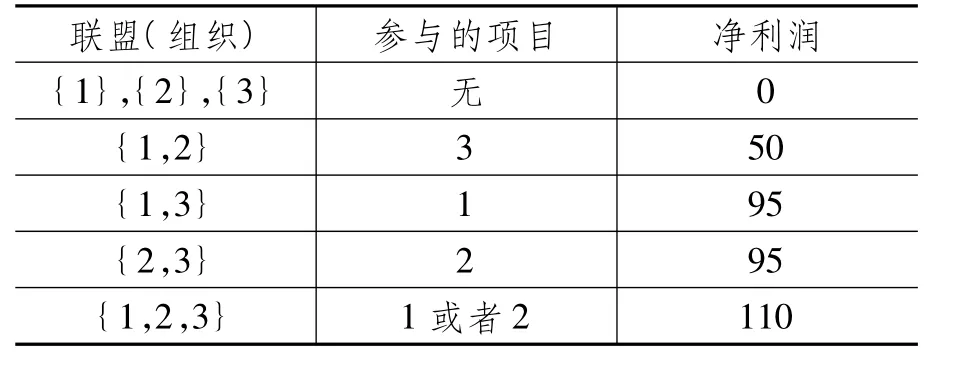
表2 不同联盟净值

如果存在核心分配(core allocation)，则任意一个核心分配必须对大结盟(the grand coalition)净利润110进行再划分，同时满足以下条件:

由条件(7)、(8)、(9)可以得出:

由于条件(6)和条件(10)相互矛盾，所以上述博弈的核心为空。这个结果表明，可能存在某些情况，使得各组织合作完成项目不是最优解。依据定义4的超可加性，不相交的联盟至少可以获得各自独立完成项目时的收益。由此可知，在预算约束的条件下，通过提升各组织间的协作能力，以此建立健全多组织联营机制，进而促使各组织协同完成应急项目。因此，通过对命题2进一步的论证得出，在预算约束下，需建立强制性事前契约来促使各参与组织协同完成应急项目。

虽然预算约束下的项目选择博弈可能存在空核心，但这不是必然结果。通过上述分析可以帮助我们找寻某种情形，使得多组织协同成为最优解。

设bj和d作为组织从项目j中获利和项目预算的基准值。则组织i的预算可以由基准值d与组织设定的某个常量δi的乘积表示。常量δi可以通过组织参与应急项目的意愿或者具有的能力加以测算。例如，作为企业组织，常量δi可以表示为企业的规模。同理，组织i的收益可以由基准值bj与常量δi的乘积表示。这意味着组织从项目中获得的收益与组织对项目的付出成比例关系。在此基础上，本文提出命题3。

命题3:如果在项目选择博弈中，满足如下条件:

(1)组织i从项目j中获得的收益

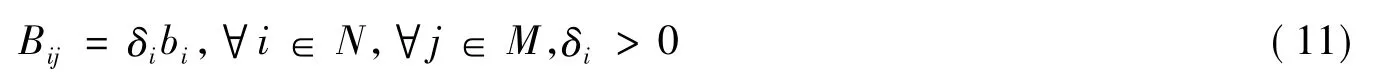
(2)组织i的预算满足

则博弈的核心非空。

证明如下:

设JS⊆M表示联盟S所选定并合作完成的项目集合;SSij(i∈S，j∈M)表示联盟中各组织所要承担的每个项目的费用。上述费用由算法1得到一个或者多个最优解。

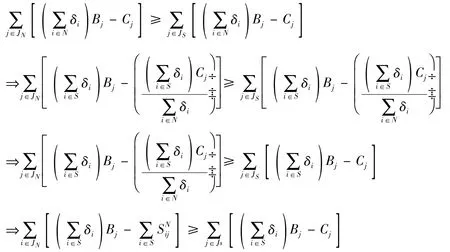
既然组织参与的项目所需的费用不会超过大结盟中各组织的项目预算，即:

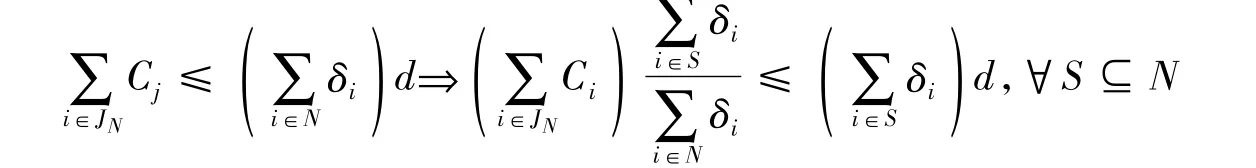
从上述不等式中可以得出，各组织所承担的应急项目费用小于各组织的项目预算，所以，上述不等式表明是可行的。

由条件(2)结合条件(1)可以得出，如果组织i从参与的应急项目中获利高于组织k，则组织i应该比组织k更加乐于承担相应的、更高的应急项目费用份额。举例说明如下:

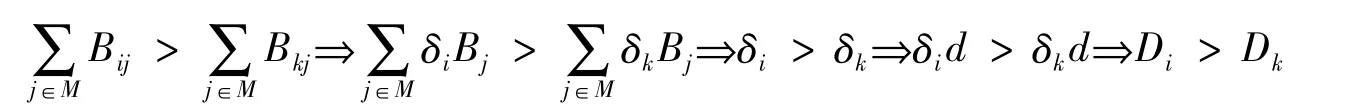
需要着重指出的是，命题3中提出的条件是严格的，对于非空核心而言，他们是充分条件，但非必要条件。一般而言，只有当组织参与应急项目的驱动力不同，同时组织从应急项目中获得的收益高于预算时，项目选择博弈存在空核心。同时，我们也无法弱化上述充分条件。例如:可以验证顺序优先级条件Bij＞Bik⇒Blj＞Blk(∀i，l∈N，∀j，k∈M)并不是非空核心的充分条件。

五、结论与建议

本文设计并给出了一个多组织协同完成应急项目的算法。基于合作博弈理论，运用上述算法对多组织协同完成应急项目时的协同策略进行了分析。在多组织协同完成应急项目时，协同策略作为最优选择时，必须满足以下任一条件:

(1)组织间不存在市场竞争，同时组织没有应急项目预算的约束。

(2)组织间不存在市场竞争，当组织有项目预算的约束时，各组织须有足够的类似的参与应急项目的驱动力，同时参与项目预算与预期项目收益呈正比，即如果组织希望从应急项目中得到较大的回报，则必须准备投入相应比例的预算。

依据上述研究结果，在应急项目管理过程中，政府为鼓励和促进多部门、企业、个人等协同完成应急项目，可参考以下建议［16，17］:

(1)应尽量减少行业内竞争者共同参与应急项目管理。当前应急项目的管理过程中，仍简单认为投入的组织和人员越多，对应急项目的实施越有利，但当参与的组织较多，特别是同行业有多个企业参与应急项目时，因企业间存在利益竞争，或将对应急项目管理带来负面影响。

(2)在财政投入不足，存在预算约束的情况下，政府应依据不同组织和部门的责任、能力和资源量等，建立强制的事前约定或者应急补充办法。当前应急项目通常采用事后的表彰奖励等方式对参与组织、个人等进行鼓励和认可，促使其今后积极参与应急项目，但仅通过上述方式仍不能满足应急项目的要求，需要通过建立事前预定，才能完善透明、持续和长效的应急管理制度。

(3)明确各组织和部门对应急项目投入的行业基准值以及不同规模组织的投入系数，只有通过事前对投入和收益关系的规治，才能实现各组织和部门对应急项目的承诺和所得利益成正比。

本文运用合作博弈理论研究得到的结论，强调了组织协同完成应急项目时，参与组织预算的约束和组织间非竞争关系对合作完成应急项目的影响。所得结论并没有考虑以下情况:

(1)组织间非对称的费用承担机制，这将体现出各组织间应急能力的差异。

(2)组织间“垂直”管理关系，例如上下级政府部门之间;产业链的上下游企业之间。本文仅假设组织间“水平”合作。

(3)由于项目收益的不确定性，不完全信息将对协同策略产生影响，例如，应对风险的态度在此将起到一定作用。

(4)组织间存在竞争时的合作博弈。

(5)合作过程中的溢出效应。

以上不足之处可作为后续研究的方向。虽然存在上述局限，但本文的研究结果对于预测应急项目管理中多组织的经济行为，以及制定规范的多组织协同战略决策仍具有现实指导意义。

［1］MITROFF I I.Crisis Management and Environmentalism:A Natural Conflict［J］.Califomia Management Review.2009，36(2):101 －113.

［2］COOMBS W T.Ongoing Crisis Communication:Planning，Managing，and Responding［M］.London:Sage Publication，Inc，1999:243－277.

［3］奥古斯丁N R.危机管理［M］.北京:中国人民大学出版社，2001:2－57.

［4］祁明亮，池宏，赵洪，等.应急管理研究现状与发展［J］.公共管理与公共策略，2006，18(4):35－45.

［5］张江华.应急管理研究［D］.上海:复旦大学，2008:9－24.

［6］张梦雨.公众参与政府自然灾害应急管理问题研究［D］.长春:吉林大学，2013:6－15.

［7］刘天虎，许维胜，吴启迪.大规模突发事件下医疗资源配置建模及算法［J］.计算机工程与应用，2010，46(29):13－17.

［8］张海龙，李雄飞，王仁彪.启发式遗传算法求解应急资源调度［J］.吉林大学学报，2010，40(3):758－762.

［9］王晓，庄亚明.基于案例推理的非常规突发事件资源需求预测［J］.西安电子科技大学学报(社会科学版)，2010，20(4):22－26.

［10］林凇.主体内生性诉求:我国应急资源管理模式的挑战与突围［J］.求索，2010(4):93－96.

［11］张立荣，冷向明.协同治理与我国公共危机管理模式创新—基于协同理论的视角［J］.华中师范大学学报(人文社会科学版 )，2008(2):67 －74.

［12］孙亚男.基于社会网络结构演化的产学研合作项目治理风险研究［D］.济南:山东大学，2012:10－17.

［13］ALOYSIUS J A.Membership in A Research Consortium:the Project Selection Game［J］.Journal of Economic Behavior＆ Organization，1999，40:325－336.

［14］HAN Z Q，DENG J Y.Emergency Process Capability Assessment Based on Stochastic Petri Nets［C］.Proceedings 2010 IEEE International Conference on Emergency Management and Management Sciences，2010:367 －371.

［15］SHAPLEY L S.Cores of Convex Games［J］.International Journal of Game Theory，1971(1):11 － 26.

［16］薛澜，刘冰.应急管理体系新挑战及其顶层设计［J］.国家行政学院学报，2013(1):10－14.

［17］丁荣贵.项目治理的基本思想［J］.项目管理技术，2007(1):72－75.