基于宏程序的非圆曲线最短加工路线设计
冯大鹏,黄耀威
( 佛山科学技术学院,广东佛山528000)
在非圆曲线轮廓的轴类的数控加工编程中,宏程序具有独特的优势。手工常规编程无法编制出非圆曲线加工程序,而应用宏程序,可通过变量赋值、运算等变化,形成插补的更新,用细段直线逼近轮廓线,并自动完成下一接点的计算及插补运动,从而完成非圆曲线加工。粗加工时,宏程序所形成的切削路线为轮廓等距线,按同一轨迹重复切削,每次切削刀具向前移动一次,直至加工完成。这种循环进给路线是由于宏程序的特点而形成的,它与常用的复合车削循环指令G70、G71 的刀具路线相差较大,而与仿形复合粗车循环指令G73 所形成的刀具路线相仿。从刀具路线优化角度来看,这种走刀方式的加工效率有待提高。
1 沿坐标轴平行切削是实现最短进给路线的有效方法
使加工程序具有最短的走刀路线是优化加工程序的主要目标之一。走刀路线是指切削加工过程中刀具相对于被加工零件的运动轨迹,它包括参与切削和不参与切削两大部分,其中不参与切削部分指空程走刀路线。对于如何减少走刀空程,特别是减少进给走刀空程的研究,已经有较多的论述。但对于参与切削部分的刀具路线,如何实现优化设计,其研究还有待深入,其目的在于使切削进给路线最短,减少切削加工时间。
在切削过程中,切削进给路线长短与切削方式有关。对工件某切削区域的粗加工,一般有两种切削进给路线选择:(1)平行轮廓的等距路线;(2)平行坐标轴的“矩形”走刀路线。这两种切削路线的长短是不同的,下面可通过实例对比进行分析。
图1 所示斜线a'为粗加工完成后的轮廓线,而a为a'的等距线。加工a 以下区域有两个方案: (1)平行a 进行切削,其刀路如图1 虚线所示,分n 次走刀完成,背吃刀量为b/n;(2)走平行坐标轴的矩形循环进给路线,其刀路如图1 实线所示。粗加工最后一刀轨迹相同。
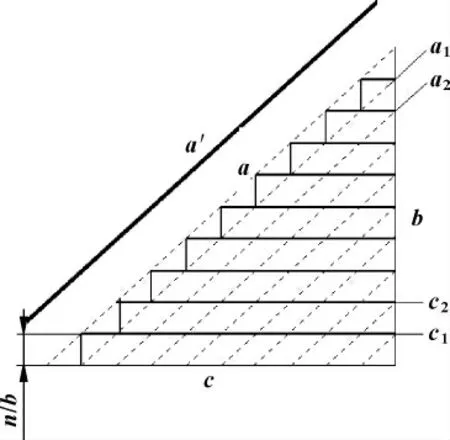
图1 两种切削进给路线
由图1 可得:
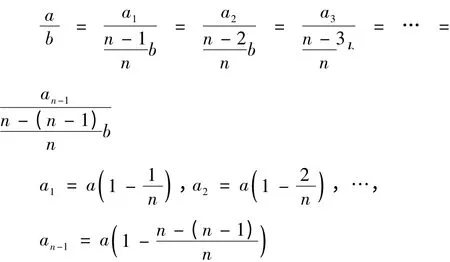
则方案一的切削路线长度总和:
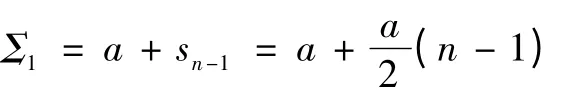
同理可得出方案二切削路线长度总和:

因为a >c,即Σ1>Σ2,故方案二的平行坐标轴的切削路线较短。
以上仅以斜线作为加工对象进行对比,对于由多段斜线和直线组成的轮廓线,当其直径呈递增变化时,上述两种加工方案的对比结果同样适用。对于各种非圆曲线及圆弧,其刀具路线长度的计算复杂,难以直接进行比较,不过,如果曲线的斜率没有出现急剧的变化,可设想由多个台阶内接这些曲线,如图2所示。
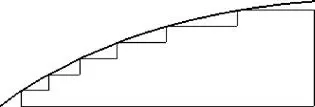
图2 曲线斜率变化不大时刀路设计
加工这些台阶可采用方案二的平行坐标轴切削方法,其效率显然比平行轮廓的切削方法要高,而且对粗加工的精度影响不大,因为之后还要沿曲线的等距线完成粗加工的最后一刀。
以上分析说明:沿坐标轴平行切削是实现最短进给路线的有效方法。为了实现平行切削,数控系统都提供一些复合循环指令如G71、G72 等,但这些指令一般只能加工由直线、圆弧组成的轮廓曲线,对于非圆曲线零件的粗加工无能为力。因此,在应用宏程序加工非圆曲线时,如果设计出一种类似于复合循环指令的沿坐标轴平行切削方法,将使切削进给路线最短,加工效率高。
2 非圆曲线零件的矩形循环路线的设计方法
设计分为两部分:第一部分是沿z 轴平行切削循环,第二部分加工非圆曲线的最后形状。
设计流程图见图3。

图3 设计流程图
3 实例及结果对比
例1 对图4 所示的A - B 段曲线进行粗加工,毛坯直径为94 mm,留精加工余量1.0 mm。z 向零点在小端“O”处。应用FAUNC 宏功能编程。

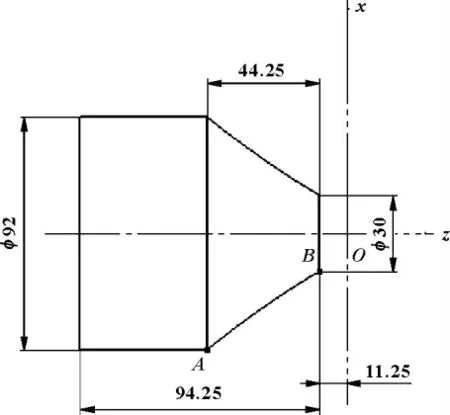
图4 示例零件
零件分别采用如下方案加工: (1)沿坐标轴平行切削方法; (2)平行轮廓切削方法。两种切削方法的刀具路线分别用虚线和细实线表示,见图5。
A1-B1为粗加工结束前最后一刀,两个方案的最后一刀路线相同,A2-B2为粗加工结束前倒数第二刀。


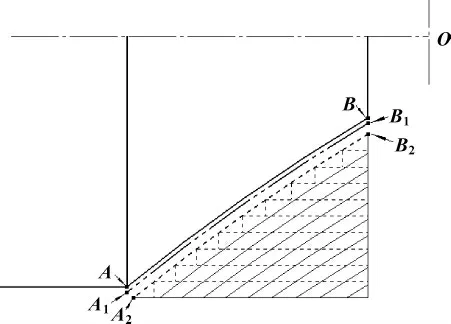
图5 两种切削方法的刀路
(1)沿坐标轴平行切削方法。
设:#1 为Z 变量,#2 为Z截止变量,#3 为X 变量。
O0001
S400M3
T0101
G0X94Z-11.25
#3 =48//X 变量赋初值
N2 G0U2//退刀
G0X94Z-11.25
#3 =#3-2.0//X 变量递减
IF [#3 LE 18.0]GOTO 5//判断X 变量
#1 = -11.25//Z 变量赋初值
#2 =SQRT [225* [[#3 -3] * [#3 -3] /144 -
1]] //计算Z 截止值
N4#1 =#1 -0.5//Z 值递减
G01X [2* #3]Z#1F100//直线插补
IF [[#1]LT #2]GOTO 2//判断Z 值是否到截止值
GOTO 4
N5 G0X94Z-11.25//准备加工A1 -B1 段
#1 = -11.25//Z 赋初值
N6 #3 =SQRT [144* [1 +#1* #1/225]] +1//计算
X
G01X [2* #3]Z#1F80//插补运动
#1 =#1 -0.2//Z 递减
IF [#1 GT-55.5]GOTO 6//判断Z 值是否到终点
G0X94Z-11.25
M30
(2)平行轮廓切削方法。
设:#1 为Z 变量,#2 为X 变量,#3 为切削余量变量,#6 为中间变量。
O0002
S400M3
T0101
G0X94Z-11.25
#3 =32//切削余量变量赋值
N2 G0X94Z-11.25
#3 =#3 -2.0//切削余量递减
IF [#3 LE 0]GOTO 5//判断切削余量
#1 = -11.25//Z 变量赋值
N4 #2 =SQRT [144* [1 +#1* #1/225]] +1//计算
X
G01X [2* [#2 +#3]]Z#1F120//直线插补
#1 =#1 -0.5//Z 值递减
#6 =2* [#2 +#3]
IF [#6 LT 94]GOTO 4//刀是否超出毛坯
GOTO 2
N5 G0X94Z-11.25
M30
两种方案的刀具路线长度总和(A2-B2以下部位)见表1。

表1 两种方案的刀具路线长度总和
从表1 可知:采用方案一切削路线明显缩短,这对于提高加工效率有较大帮助。
4 结束语
通过设计一种近似于矩形的循环进给路线,实现粗加工垂直进刀→水平切削→退刀→再进刀的加工循环,使加工路线较短,效率提高。这种加工方法对于单调变化的非圆曲线,如双曲线、对数曲线等的加工非常有效,而对于非单调变化的非圆曲线加工,单一的矩形循环进给路线并不适用,此时需要采用平行轮廓的等距路线,其优点是节省了换刀时间,一次加工完成。但由于零件外圆含有凹弧,为避免刀具副切削刃与工件发生干涉现象,刀具副偏角一般较大,而副偏角加大不利于刀具强度的提高和加工散热,影响刀具寿命,同时限制了切削用量,不利于加工效率的提高。从优化加工路线角度综合衡量,需寻找更加合理的加工方案的配对组合。
【1】王娟平.回转体类零件的数控加工工艺路线及工序进给路线的设计[J].新技术新工艺,2011(6):56 -58.
【2】陈光明.数控加工中工艺路线设计原则及方法[J]. 组合机床与自动化加工技术,2005(11):69 -72

