三相电压型PWM整流器的稳定性研究

钟炎平，陈耀军，吴胜华

(空军预警学院，湖北 武汉 430019)

0 引言

三相电压型PWM整流器与传统的不控整流器和相控整流器相比，具有单位功率因数、网侧电流正弦化、能量可实现双向流动等优点，因此，PWM整流器得到越来越广泛的应用，并成为研究的热点。

对PWM整流器的研究，目前主要集中在整流器工作在整流状态下如何提高系统的动态及稳态性能上，例如克服非线性以及电流耦合影响的研究。然而，由于整流器可四象限运行，其可以工作在整流状态或有源逆变状态，能量可实现双向流动，有些控制策略在整流状态下可能是最优的，但在其它不同的工作状态下，控制性能就可能变差，系统产生振荡甚至不稳定。因此，对在不同负载性质、不同工作状态下整流器的性能的分析和研究具有重要意义。本文对PWM整流器在整流和有源逆变两种工作状态下的稳定性进行了研究，研究结果有助于对PWM整流器稳定性的深入认识，对整流器的设计具有一定的参考意义。

1 PWM整流器的数学模型

三相电压型PWM整流器如图1所示。

PWM整流器广泛采用在d－q同步旋转坐标系的双闭环控制，在一定的条件下，电流内环控制可认为是理想的，为研究稳定性，只需研究电压外环的稳定性。为此先建立PWM整流器的电压方程。

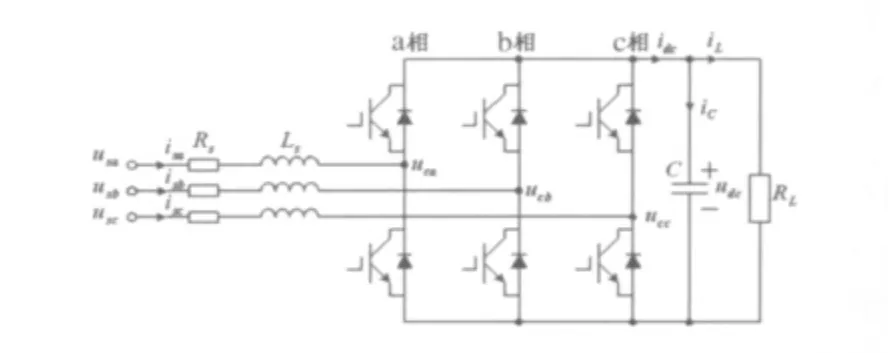
图1 PWM整流器原理图

根据功率平衡原理，当忽略交流侧电感及整流器桥路自身的损耗[1]，交流侧有功功率 pac应与直流侧功率pdc相等，即:

在d－q同步旋转坐标系中，有:

式中usl、isl(l=d，q)分别为d－q同步旋转坐标系下的电源电压和输入电流，IL为负载电流。上述分析忽略了交流侧电感的等效电阻Rs的损耗及桥路功率器件的导通和开关损耗。

在d－q同步旋转坐标系中，通常将d轴定向于与电网电压矢量同方向上，若三相对称电源相电压的最大值为Um，则:

将式(2)代入式(1)，有:

显然，方程(3)中，输出电压udc和有功电流isd之间存在着非线性关系，为便于分析，采用微偏线性化的方法对方程进行线性化处理[2－4]，得到直流电压相对于有功电流的扰动传递函数为:

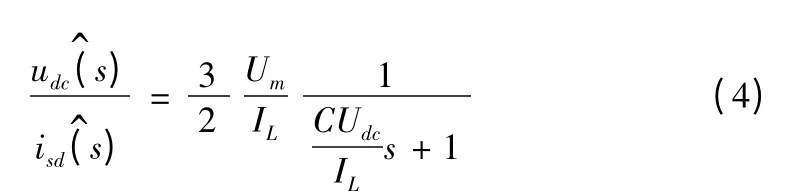
在上述推导中，假设负载的电流为IL，当负载为阻性时，吸收功率，IL＞0，系统工作在整流状态;当负载为有源负载时，产生功率，IL＜0，系统工作在逆变状态。

研究PWM整流器在逆变工作状态即负载为有源负载情况的稳定性是非常有意义的。例如，若PWM整流器的负载为感性负载而突然断开时，或是当整流器的指令输出电压突然由高变为低时，或者负载为另一PWM逆变器驱动一个频繁改变转向的电动机，逆变器将电动机的制动能量回馈到直流端，为保持直流电压的恒定，则PWM整流器工作在逆变状态。在以上n种情况下，可认为整流器的负载为有源负载，也就是说在PWM整流器工作时，负载为有源负载的情况经常发生，整流器的工作状态是在整流与有源逆变之间频繁转换的[5]。

2 负载对稳定性影响的研究

PWM整流器在d－q同步旋转坐标系的控制中，典型的控制方法是电压外环采用线性PI控制器，若整流器的电压方程采用微偏线性化处理所得到的线性方程式(4)，则电压控制框图如图2所示。

设PI控制器的传递函数为:

图2 PWM整流器电压控制

在负载电流大于零、等于零和小于零三种情况下，根据式(5)作出系统随比例增益Kpu变化的根轨迹，如图3所示。仿真参数为:Udc=600 V，C=3 200 μF，Um=311 V，Klu=5。

从系统根轨迹可以看出[6]，当负载电流大于零时(IL=12 A)，根轨迹始终位于复平面的左半平面，系统是稳定的;而在同样参数的情况下，当负载电流小于零时(IL=－12 A)，根轨迹有部分位于复平面的右半平面，系统不稳定。当负载电流从大于零向等于零和小于零变化时，根轨迹逐步从左半平面向右半平面移动，系统由稳定变成不稳定。

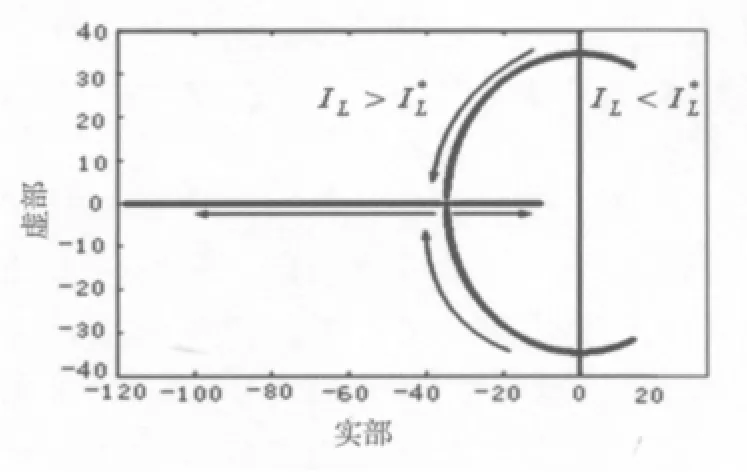
图4 系统特征根随ⅠL变化时的轨迹

图4 所示为对于给定的KPu和 KIu，负载变化时系统的根轨迹，显示了负载变化对系统性能的影响。在给定参数的情况下，有一临界负载电流(由式(5)得，当 IL＜时，根轨迹位于右半平面，系统不稳定;当IL＞I*L时，根轨迹位于左半平面，随着负载电流绝对值从大减小到零(此时IL＜0)并从零逐渐增大(此时IL＞0)，系统根轨迹向实轴交汇，表明系统超调减小，稳定性增强。

由以上分析可见，当电压环采用线性PI控制时，系统存在一个随负载变化的极点，因而，PWM整流器的稳定性和动态性能与负载情况有很大的关系。同样的控制参数，在负载不同的情况下，系统的动态响应性能也不相同，甚至可能变得不稳定。

引起这一问题的原因是由于系统存在一个可变的极点，该极点随负载电流变化而变化，而线性PI控制不能消除这一极点，也就无法消除这一极点对系统性能的影响，这一点是在设计整流器控制参数时必须认识到的。

3 有源逆变状态下，比例系数的选取与稳定性

从上一节的分析看出，当PWM整流器工作在有源逆变状态下，随着PI控制器比例增益Kpu的变化，闭环传递函数的部分特征根位于复平面的右半平面，系统不稳定。因此，必须仔细选择比例增益，使系统工作在稳定状态。

对于一个二次多项式，根据二次方程根的性质可知，当多项式系数有一项小于零时，多项式对应的方程至少有一个根大于零，令式(5)中分母的一次项系数小于零，可得:

图3 不同负载电流时，系统的根轨迹

若式(6)立，则系统闭环极点位于右半平面，系统不稳定。可见，要使系统稳定，应选取较大的比例增益，使比例增益大于其临界值，且负载电流的绝对值越大，比例增益也应取的越大。图5所示为固定有源负载(IL=－12 A)条件下系统的特征根随 Kpu变化时的轨迹。可以看出，当Kpu＜时，特征根位于右半平面，系统不稳定;随着 Kpu的增大，根轨迹从右半平面向左半平面移动;当Kpu＞K*pu时，根全部位于左半平面，系统稳定。而且随着Kpu的增大，系统的根从虚轴正负轴同时向实轴靠近交于实轴，然后向实轴两端延伸。由此可见，要想保持系统的稳定必须适当增加Kpu。

图5 系统特征根随Kpu变化时的轨迹

图6 不同Kpu时输出电压波形

对采用线性PI控制器时比例增益 Kpu对稳定性的影响，用MATLAB/Simulink进行了仿真研究。负载电阻在2.5秒时从正变为负，使整流器从整流状态变为逆变状态，在不同的Kpu时，输出电压的波形如图6所示。从仿真结果看出，随着Kpu从大于临界值变到接近临界值再变为小于临界值，输出电压从稳定变为振荡直至不稳定。仿真结果验证了以上分析。

在逆变状态时，PI调节器要选择较大的比例增益，才会使系统更加稳定，这是由于增益越高，可以使直流侧的能量向电网回馈越快的缘故。

以上研究表明，PWM整流器在有源逆变工作状态下，当采用线性PI控制时，比例增益的选取直接决定了系统的稳定性。只有当比例增益大于临界值时，系统才稳定。由于整流器的工作状态是在整流与有源逆变之间频繁转换的，在设计PI控制器参数时，不能仅考虑整流工作状态，而必须考虑有源逆变工作状态。在整流状态下，过大的比例增益会引起系统超调和振荡;在有源逆变状态下，过小的比例增益会使系统不稳定。因此，应根据负载变化范围以及要求的超调量、过渡过程时间等指标设计PI调节器的比例和积分系数，同时检查比例系数是否满足式(6)的稳定性要求。当系统不稳定时，应合理调整比例系数。

4 结束语

在PWM整流器工作时，负载为有源负载的情况经常发生，整流器的工作状态是在整流与有源逆变之间频繁转换的，对整流和有源逆变工作状态下的稳定性研究具有实际意义。

PWM整流器在采用线性PI控制时，稳定性和动态性能与负载有关。系统存在一个随负载变化的极点，因而系统的动态性能随负载的不同而改变，并且在有源逆变工作状态下系统存在不稳定极点，这是在设计整流器控制参数时必须充分认识到的。

比例增益的选取直接决定了系统的稳定性。比例增益在整流状态下不能太高，在有源逆变状态下不能太低，因此在设计参数时应综合考虑。参考文献:

[1]张崇巍，张兴.PWM整流器及其控制[M].北京:机械工业出版社，2003.

[2]胡跃明.非线性控制系统理论与应用[M].北京:国防工业出版社，2002.

[3]P.Verdelho，G.D.Marques.DC voltage control and stability analysis of PWM voltage type reversible rectifiers[J].IEEE Transactions on Industrial Electronics，1998，45(2):263 －273.

[4]Y.Ye，M.Kazerani，V.H.Quintana.A novel modeling and control method for three－ phase PWM converters[C].PESC.2001 IEEE 32th Annual.2001，1:102 －107.

[5]J.Espinoza，G.Joos，M.Perez，et al，Stability issues in three － phase PWM current/voltage source rectifier in the regeneration mode[C].ISIE＇2000，Cholula，Puebla，Mexico，453 －458.

[6]吴麒.自动控制原理[M]，北京:清华大学出版社，1990.