基于matlab的滚动轴承智能监测应用实例分析
张雅楠
(西南交通大学,四川 成都 611756)
0 引 言
滚动轴承广泛用于各类旋转机械[1]。据统计,旋转机械中约30%的故障是由滚动轴承损坏引起[2],因此,研究滚动轴承的故障诊断技术十分重要。若能通过监测轴承产生的异常信号、实时快速诊断出轴承的故障,从而及时维修更换轴承,则可有效减少企业经济损失,提高企业生产效率。
现在普遍的监测方法主要有:人工监测、空转实验、仪器监测等。监测效率最高、且精确的是用仪器监测滚动轴承运行状态。本文采用振动传感器和仪器对滚动轴承运行状态进行智能化监测。
1 信号的采集和基于matlab的信号处理分析
预先采用振动传感器对正常轴承和同型故障轴承分别进行数据采集。测取的滚动轴承振动信号接入电荷放大器放大信号,再经A/D 卡转换为计算机可以识别和处理的数字信号,再经DSP信号处理器对数据处理后接入计算机。形成正常数据采集样本和故障数据采集样本(实际处理中尽可能多的采集样本,以保证结果的准确性)[3]。
matlab 是高性能的数值计算和可视化软件,它集数值计算、信号处理、图形分析等功能于一体,被称演算纸式的语言。计算机上可用matlab编程实现以下功能:时域分析、频域分析、提取有效特征向量[4]。使用matlab分析处理的过程为:将采集的数据导入matlab,并绘制出时域图像;先对时域的信号进行快速傅里叶变换,通过读出数据x,直接调用fft函数,并用plot函数绘出幅频曲线图,见图1。
现以故障轴承采集的数据G2015为例,(本文采集到故障轴承编号:G2015、G3015、G2515、G20610、G25610、G30610 的运行数据;正常轴承编号:Z2015、Z3015、Z2515、Z20610、Z25610、Z30610 的运行数据)进行实例分析,相关matlab编程语言如下:
n=100 000;%采集的数据数
fs=10 000;%采样频率
t=0:1/10 000:9.999 9;%定义时间变量,采样间隔
m=G2015-(sum(G2015)/n);%零均值化
subplot(2,1,1);
plot(t,m);%作时域内的图像
x=fft(G2015,n);%进行fft
y=abs(x);%求幅值
f=(0:n-1)*fs/n;%横坐标频率的表达式
subplot(2,1,2);
plot(f,y);%作频谱图
axis([0 5000 0 2500])
G2015时域与频域的分析结果,见图1。通过对六组数据的分析,得到了监测数据的时域和频域图。从图看出,故障轴承和正常的时域图和频域图有很大的区别;但仅凭人的观察很难完全判断准确,需对收集数据的时域和频域图进行特征值的提取,并进行归一化处理形成一种模式。通过将提取到的特征值输入神经网络进行训练,以此利用神经网络可对轴承是否故障进行准确判断。
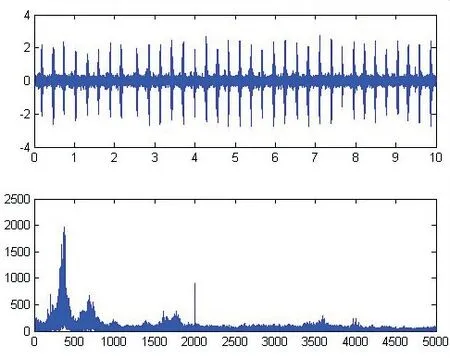
图1 G 2015时域与频域的分析结果
1)对信号的时域和频域提取特征值:信号的时域特征一般包括:均值、方差、均方根、峰值、峰值因子、峭度系数、波形因子、裕度因子、脉冲因子。其在matlab中编程如下:
fc=sum((m-jz).^2); %方差
jfg=sqrt(sum(m.^2)/n); %均方根
fz=(max(m)-min(m))/2; %峰值
fzyz=fz/jfg; %峰值因子
qdxs=sum(m.^4)/((jfg.^4)*n);%峭度系数
bxyz=(jfg*n)/sum(abs(m)); %波形因子
ydyz=fz/(sum(sqrt(abs(m)))/n).^2; %裕度因子
mcyz=(fz*n)/sum(abs(m)); %脉冲因子
MAX=max(GY) %找出数组(命名为GY)中的最大值
MIN=min(GY) %找出数组(命名为GY)中的最小值
GYJZ=(GY-MIN)/(MAX-MIN)%求这组数据归一化之后的数组
归一化处理后的各项数据形成一个数据表格进行对比,利用特征值相差特别明显、重复性好的特征,对神经网络进行训练。通过分析,选取峰值、峰值因子、峭度系数、波形因子、裕度因子对神经网络进行训练。
2)以故障轴承G2015 与正常轴承Z2015 为例,对其频域进行特征值提取,见图2。将所有六组数据的频域特征值进行归一处理,并且列表分析。通过分析选取200 Hz、2000 Hz、3600 Hz、4000 Hz 训练神经网络,从而利用神经网络识别故障轴承。分析对比各个已知故障轴承的故障原因,并将数据送人神经网络训练得到相应的输出,之后就可对未知故障轴承进行诊断。
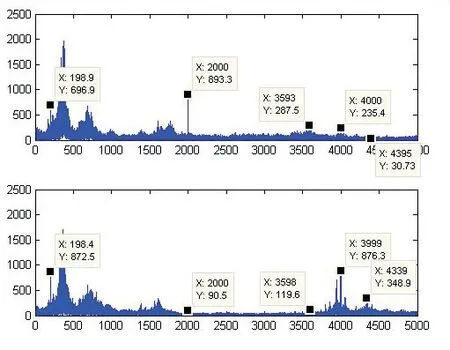
图2 特征值提取
2 人工神经网络在故障诊断中的应用
人工神经网络(NN,Neural network)是由一组功能简单的信息处理单元在一定连接方式下构成的动力学系统,它以并行机制处理数据信息,具有自适应性、自学习、自组织的能力。一个基本的神经网络包括:神经元、网络拓扑结构、学习规则(训练法)[5]。神经元的功能是求得输入向量与权向量的内积后,经一个非线性传递函数得到一个标量结果。神经元可形象地作为一个阀门,经对输入向量进行加权求和后,再与预先设定的阀值进行比较。如果大于阀值则输出某一结果,小于阀值输出另一结果。
神经元网络结构由输入层、输出层、若干隐含层构成:每一层都由若干个节点组成,每个节点表示一个神经元,上层节点与下层节点之间通过权连接,层与层间的节点采用全互联的连接方式,每层内节点之间没有联系。
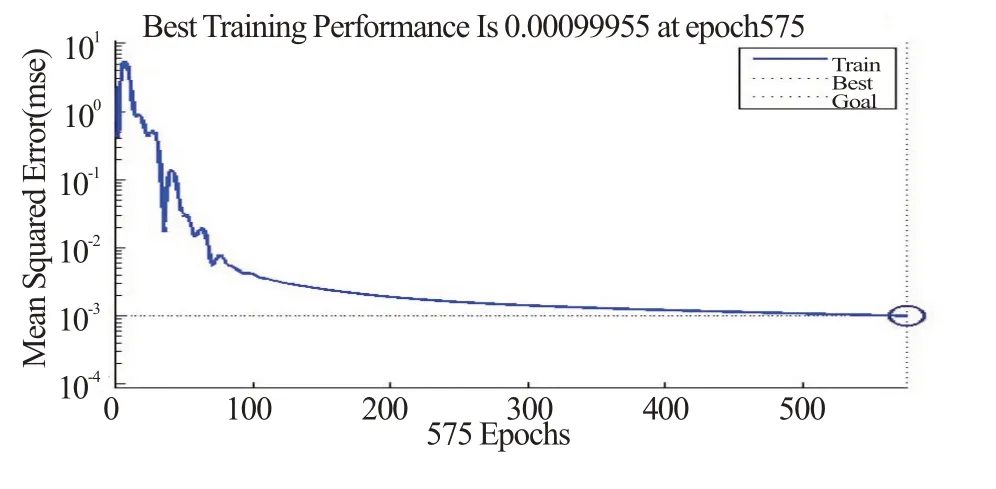
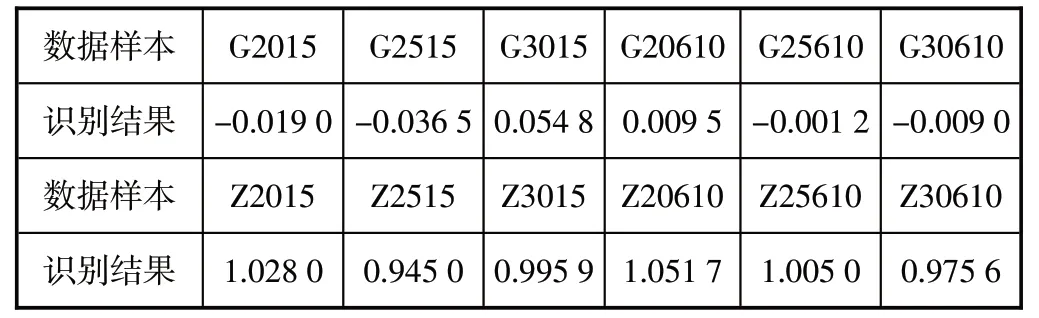
目前,人工神经网络的实际应用中,大多数的模型采用前馈反向传播网络(Back-Propagation-Ne tw ork,BP 网络)或其变形。标准的BP 网络采用梯度下降算法,对非线性可微分函数进行权值训练的多层网络。对于一个三层BP 神经网络,只要隐层节点数足够多,就有逼近任意复杂的非线性映射能力。通用的隐含层神经元数的确定经验公式有[6]:i= n+m +a.式中:i为隐含层神经元的个数;n为输入层神经元的个数;m为输出层神经元的个数;a为常数、且1 1)训练前初始参数的选取。初始权值的选择一般在(-1,1)之间的随机数。学习速率的选择一般在0.01~0.80 之间。期望误差值一般作为对比,可同时对2 个不同期望误差值的网络进行训练,最后通过考虑综合因素采用其中一个网络,本系统BP网络期望误差值为0.01。 2)权值的训练。将已提取出的故障轴承和正常轴承的时域与频域特征归一化后的数据输入神经网络。建立一个3层BP神经网络,根据特征矩阵确定输入的特征为9项,即有9个输入神经元。通过经验公式计算隐层的神经元数量约为13。输出层设为一个神经元,当输入为故障轴承数据时,显示结果为0。mat⁃lab编程如下: P=gy' %将归一化后的数据导入matlab,并且命名为‘gy’。 T=[0 0 0 0 0 0 1 1 1 1 1 1]; % 创建一个新的前向神经网络 net_1=newff(minmax(P),[n,1],{'tansig','purelin'},'traingdm') %建立新的神经网络net,newff(输入,输出,{隐层数量及该层的节点个数},{传输函数名},训练函数); % 当前输入层权值和阈值 inputWeights=net_1.IW{1,1} inputbias=net_1.b{1} % 当前网络层权值和阈值 layerWeights=net_1.LW{2,1} layerbias=net_1.b{2} % 设置训练参数 net_1.trainParam.show=50; net_1.trainParam.lr=0.05; net_1.trainParam.mc=0.9; net_1.trainParam.epochs=10000; net_1.trainParam.goal=1e-3; % 调用TRAINGDM 算法训练BP 网络 [net_1,tr]=train(net_1,P,T); % 对BP 网络进行仿真 A=sim(net_1,P); %测试 x=[测试数据]'; sim(net_1,x) 神经网络训练结果,见图3。从图看出,对神经网络训练到第575 次时达到训练精度;收敛较快,效果较好。 图3 神经网络训练结果 3)对建立的神经网络进行仿真测试。在Matlab中设计完整的BP 网络权值训练程序。训练结束后,通过查看BP 网络输出层的输出值是否符合预期要求,可分析出是否建立了较理想的故障诊断BP 网络模型[7]。分别将6 组正常轴承和6 组故障轴承的特征值输入神经网络,利用matlab仿真语句: % 对BP 网络进行仿真 A=sim(net_1,P); %测试 x=[测试数据]'; sim(net_1,x) 表1 对输入数据进行识别的结果 从表1可看出,故障轴承的输出值均在0左右,正常轴承的输出值均在1左右。建立的神经网络收敛性较好,误差在范围内。 滚动轴承状态监测是现代生产中的重要一环。对滚动轴承的运行状态进行智能化监测,可有效地减少企业损失、节约人力物力。通过采集轴承运行过程中的振动信号,将信号输入电脑,进行时域和频域的特征值提取,建立人工BP 神经网络进行智能化识别,就能准确检测轴承的状态,根据训练的数据来源,不仅能识别本文所提到的故障和正常鉴别,还能识别到底是什么故障,能为维修工作提供准确信息。达到滚动轴承智能化监测的目的。 [1] 肖军.滚动轴承常见故障及诊断[J].工程机械与维修,2007(12):18-21. [2] 艾莉,华静.基于多传感器信息融合的滚动轴承故障诊断[J].轴承,2012(3):47-49. [3] 戴静君,刘丽华,薛庆齐,等.滚动轴承故障诊断中振动信号的采集[J].北京石油化工学报,2008(6):32-38. [4] 孙苗钟,赵鹏.基于MATLAB 的振动测试信号处理与分析系统设计与实现[J].工程技术与产业经济,2008(10):44-48. [5] 李翔著.从复杂到有序-神经网络智能控制理论新进展[M].上海:上海交通大学出版社,2001. [6] 焦淑华. BP神经网络预测的MATLAB实现[J].金融理论与教学,2009(3):55-56. [7] 张凤蕊,朱清慧.小波遗传神经网络在大型直线振动筛故障诊断中的应用[J].矿山机械,2012(8):64-68.3 BP 神经网络预测的matlab实现
4 结束语

