基于Bayes方法的雷达系统可靠性评估

丁 贝

（海军装备部，陕西 宝鸡 721000）

0 引 言

现代质量观念中的可靠性，已成为产品的一项重要基本质量标志[1]。对于雷达系统而言，其可靠性直接影响到雷达系统能否正常实现预定功能和使用要求。因此，必须在雷达系统定型前对其可靠性进行评估，以检验是否满足可靠性要求。可靠性评估就是根据产品的可靠性结构（系统和单元间的可靠性关系）、产品的寿命分布模型、产品的验前信息和试验数据，利用概率统计方法对产品可靠性的特征量进行统计、推断、决策，包括点估计和区间估计。本文采用著名的Bayes方法，利用较少的实验数据，对雷达系统的可靠性进行合理评估。

1 Bayes可靠性评估方法

1.1 可靠性评估的定义

可靠性评估是对元件或系统的工作（或固有能力或性能改进措施）效果是否满足规定的可靠性准则进行分析、预计、认定的过程，它是衡量产品可靠性是否达到预期设计目标，从而促进产品可靠性增长的重要方法。系统的可靠性是在规定条件下和规定时间内无故障完成规定功能的概率。系统的可靠度函数为[2]：

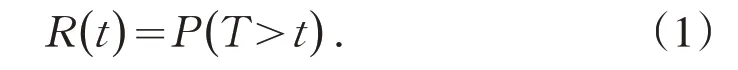
式中：T为系统正常工作的寿命时间，是随机变量；t为要求的任务时间。对系统的可靠性评估是要寻求如下概率方程的系统可信置信下界RL值：

式中：γ 为置信度，通常在产品研制初样阶段取0.6~0.7，正样定型阶段取0.8~0.9。

任何大系统均由若干分系统组成，各分系统由很多单机和部件组成，各单机和部件由很多元器件组成，它们之间的关系可以建立一个金字塔模型。因此，对系统的可靠性评估，可以从金字塔的最下层、依次向上进行，局部进行各层次的可靠性评估、直至整个系统，先对单元的可靠性进行评估，再逐级评估整个系统的可靠性。

1.2 B ayes方法

贝叶斯方法进行可靠性评估，能够准确体现金字塔式逐级综合的思想，是由单元到系统的信息融合过程。对指数寿命型产品的可靠性评估，采用著名的贝叶斯公式如下：

式中：失效率λ 为随机变量，且赋予一种适当形式的概率分布g(λ) ，由元件的试验数据拟定一个抽样分布f( x )λ ，联合参数λ 的验前分布和抽样分布，给出λ的验后分布，进而对元件的可靠性做出验后推断。采用Bayes方法对系统的可靠性进行综合评估的过程如下：1）系统可靠性框图的建立以及系统、分系统、单元的寿命分布的确定。2）积累获取系统单元的可靠验前信息，并对其进行可信性分析；依据已获取的单元验前数据，得到样本似然函数。3）根据已获取的单元验前信息，确定参数的验前分布。4）根据步骤2）、3），运用Bayes公式，计算单元可靠性参数的验后分布，进而算得单元可靠度的验后分布和验后矩。5）分别将组成系统的各单元可靠度的验后矩，代入系统结构函数算出系统可靠度的验前矩，并由此算出系统验前分布中的参数。6）类似步骤2）、4）对系统试验数据进行处理，算出系统可靠度的验后分布。7）依据系统可靠参数的验后分布，对系统的可靠性进行评估，包括可靠性参数的点估计、置信区间估计及假设检验等，见图1。

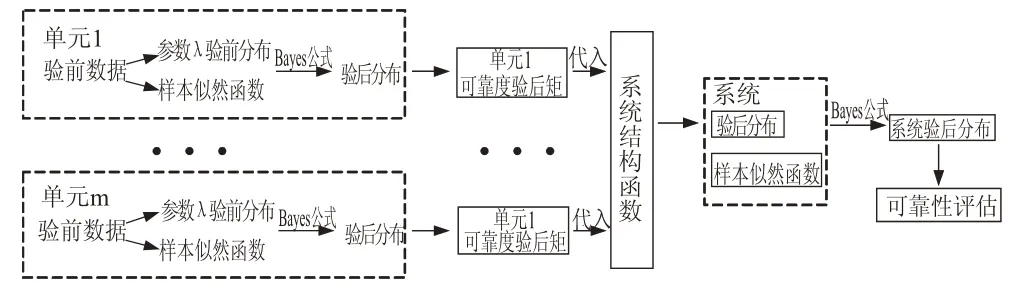
图1 Bayes可靠性评估过程图

2 雷达系统可靠性评估模型

雷达系统由天馈线、天线转台、信号处理机、数据处理机及显控、伺服控制、配电等分机组成，根据雷达系统工作原理，导出雷达系统各单元之间的功能关系，并由此构建雷达系统的可靠性框图，见图2。图2雷达系统由相互独立的指数寿命分布的分机组成，可靠性模型是串联模式，任何一个单元发生故障，雷达系统都算发生故障一次，需要维修，其失效率服从指数分布。

图2 雷达基本可靠性框图

对于串联模式可靠性模型的整机失效率应为各个单元失效率之和，雷达系统的整机失效率可由下式算得：

因此，雷达系统的平均故障间隔时间为：MTBF=1 λS.

对指数型寿命分布的可靠性分析中，对于失效率λ 广泛采用伽玛验前分布Γ(α， β )，利用Bayes 公式，可以得到雷达系统失效率λs的验后均值和方差[3]：

式中：z 为试验中产品失效次数；τ 为试验时间；j 为元器件数量。利用伽玛函数：

3 结束语

根据上述基于Bayes 方法的可靠性评估模型，可以利用较少的现场试验数据对雷达系统的可靠性进行评估，从而更加真实反应雷达系统的可靠性水平，能为雷达系统的设计定型提供参考，并能促进雷达系统研发、生产、后续使用中的可靠性管理工作。

[1] 张士峰.Bayes 可靠性评估方法评述[J].飞行器测控学报，2000(19)：32-36.

[2] 郭维长.卫星电子系统可靠性评估（Bayes 方法）[J].航天器工程，1997(6)：44-47.

[3] Merrill l.Skolnik. 雷达系统导论[M]. 北京：电子工业出版社，2010.