GNSS点位误差转换方法研究

孙小荣，张书毕，卞和方，刘支亮

(1.宿迁学院建筑工程系，江苏宿迁223800;2.中国矿业大学国土环境与灾害监测国家测绘地理信息局重点实验室，江苏徐州221116)

一、引 言

在测量中，空间点的位置常在地心坐标系和参心坐标系下表示，两者都有大地坐标系、空间直角坐标系和高斯平面直角坐标系3种常用表达形式［1-3］。GNSS定位模型一般是在空间直角坐标系下建立的，以P点为例，解算的定位结果包括点的坐标(X，Y，Z)和方差-协方差阵DXYZ。DXYZ的形式如下［4-6］

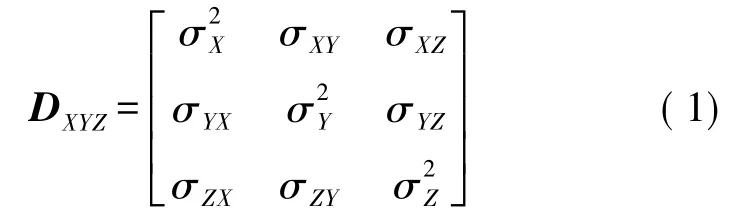
目前最常用的点位误差度量方法是Helmert表示法，P点的点位误差可表示为［4-6］

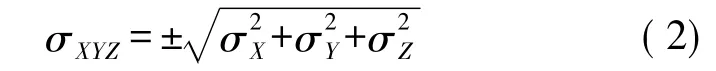
在实际应用中，GNSS定位除进行不同表达形式之间坐标值的转换［1-3］，还需进行表达形式之间的误差转换［3，7-10］。文献［7—8］给出了空间直角坐标(X，Y，Z)与大地坐标(B，L，H)之间的全微分及误差转换公式，式中d B、d L以角度为单位，d H以长度为单位。以角度量表示的误差在数值上非常小，且同一经差所相应的平行圈弧长在不同纬度处相差较大，不利于实际应用，且系数矩阵较为复杂［9-10］。文献［9］借助子午圈曲率半径和平行圈半径将B、L的角度量误差转换为以长度为单位的误差(等效长度量误差)，但文献［9］的推导过程较复杂，本文将推导简化公式，并从理论证明和算例验证该公式可代替现有的空间直角坐标系与高斯平面直角坐标系之间复杂的误差转换公式。

二、(X，Y，Z)与(B，L，H)误差转换

1.(B，L，H)误差转换为(X，Y，Z)误差

(X，Y，Z)与(B，L，H)之间的关系式为［1-3，8］

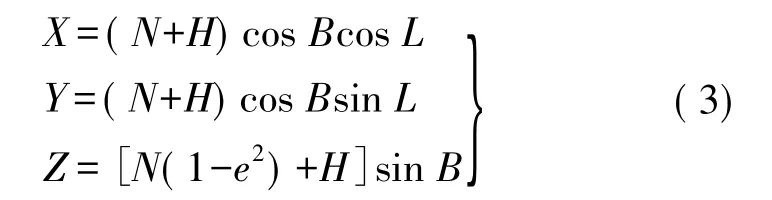
式(3)的全微分形式为［3，8，11］

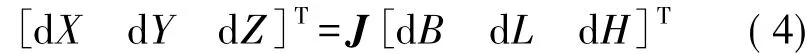
式中，dX、dY、dZ、dH以m为单位;dB、dL以秒为单位;

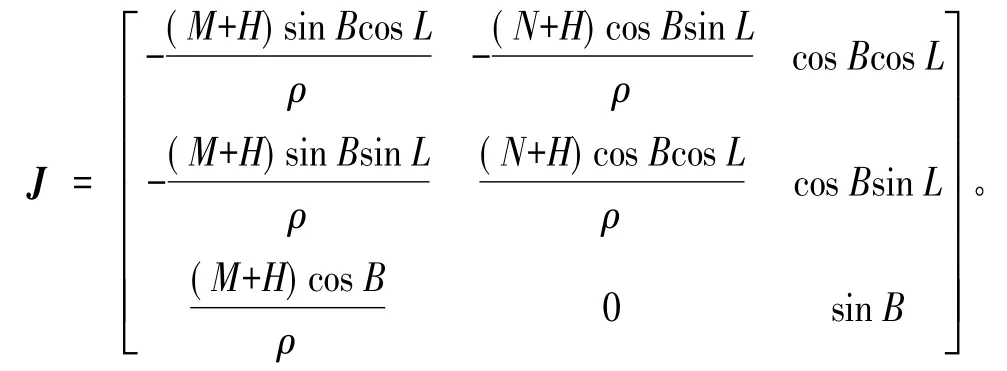
其中，M为P点法线与椭球面交点的子午圈曲率半径，M=a(1－e2)/W3;ρ=180/π×3600。

由式(4)，根据误差传播定律，P点在空间直角坐标系下的方差协方差阵为

P点在空间直角坐标系下的DXYZ和点位误差表示方法见式(1)、式(2)。

2.(X，Y，Z)误差转换为(B，L，H)误差

因 J 是可逆矩阵，由式(4)可得［3，8，11］

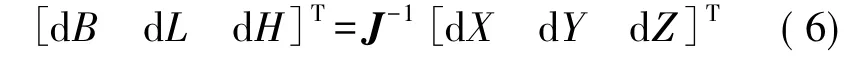
式中

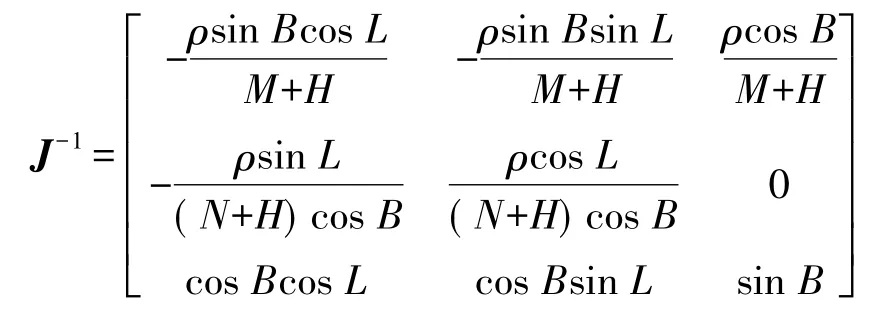
由式(6)，根据误差传播定律，P点在大地坐标系下的方差协方差阵为

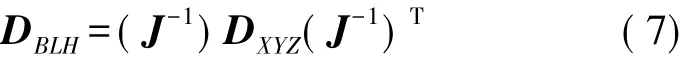
三、(x，y)与(B，L)误差转换

1.(B，L)误差转换为(x，y)误差

当略去l的4次及以上项，高斯投影坐标正算公式为［1-3，8］

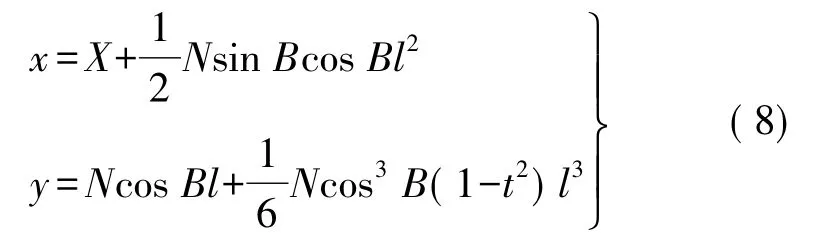
式(8)的全微分形式为［8］

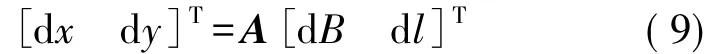
式中，d x、d y以 m为单位;d l以秒为单位;A=

其中

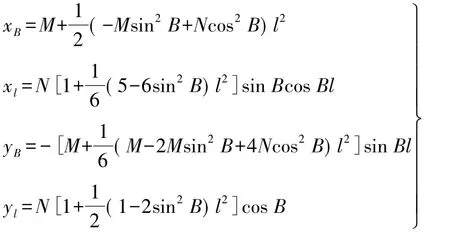
由式(9)，根据误差传播定律，P点在高斯平面直角坐标系下的方差-协方差阵为［4-6］

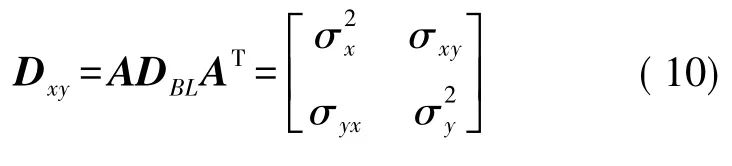
P点在高斯平面直角坐标系下的点位误差可表示为［4-6］

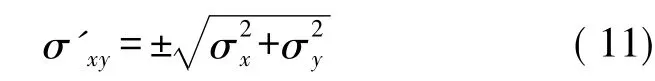
2.(x，y)误差转换为(B，L)误差

因A是可逆矩阵，由式(9)可得［8］

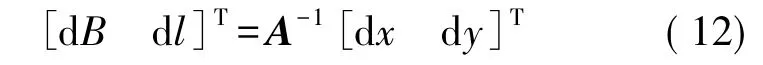
式中

由式(12)，根据误差传播定律，P点在大地坐标系下的方差-协方差阵为

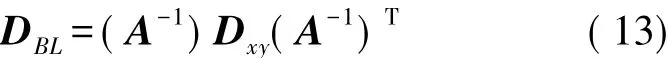
四、(X，Y，Z)与(x，y，H)误差转换

1.(X，Y，Z)误差转换为(x，y)误差

转换过程分两步进行：首先将(X，Y，Z)误差转换为(B，L，H)误差;然后将(B，L)误差转换为(x，y)误差。综合式(6)、式(9)，得

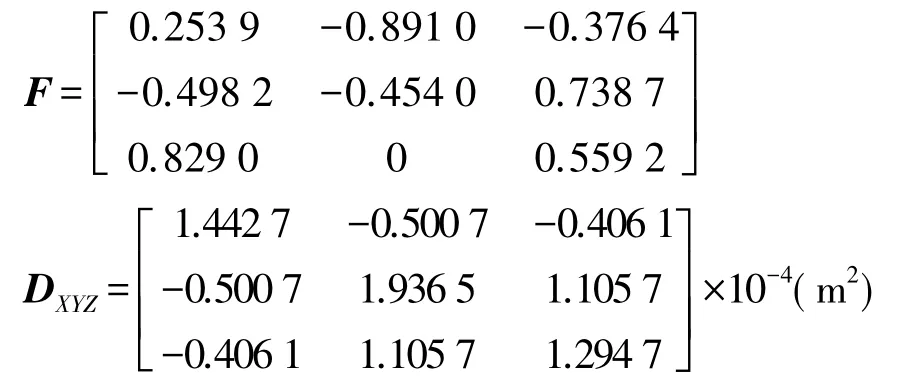
2.(x，y，H)误差转换为(X，Y，Z)误差

转换过程分两步进行：首先将(x，y)误差转换为(B，L)误差;然后将(B，L，H)误差转换为(X，Y，Z)误差。综合式(4)、式(12)，得

式中，C=JF;F=diag(A－11);DxyH=diag(Dxy)。其中，σH为P点的高程误差，diag()表示对角矩阵。

五、(X，Y，Z)与(N1，E，U)误差转换

1.(N1，E，U)误差转换为(X，Y，Z)误差

因P点的子午圈曲率半径M'=M+H，所在平行圈半径r=(N+H)cos B，令dN1=M'd B/ρ、d E=r d L/ρ，则d N1、dE分别表示P点的角度量误差引起的沿子午圈方向(南北方向)和平行圈方向(东西方向)的长度量误差。由于dB很小，在［B，B+d B］区间内完全可视M'不变，这相当于以子午圈和平行圈上两个微小的曲线长度来表示P点的南北方向和东西方向误差。则

垂直方向(法线方向)误差用d U表示，则

将式(16)～式(18)代入式(4)，得

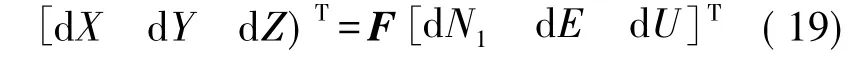
式中

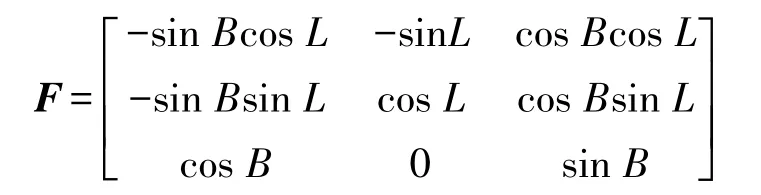
由式(19)，根据误差传播定律，P点在空间直角坐标系下的方差-协方差阵为

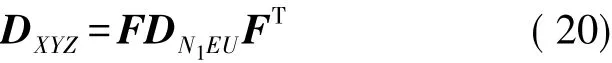
2.(X，Y，Z)误差转换为(N1，E，U)误差

因T为正交矩阵［9］，其逆矩阵等于转置矩阵。由式(19)可得

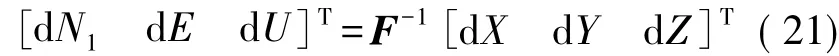
式中

由式(21)，根据误差传播定律，P点在大地坐标系下的方差-协方差阵为［4-6］

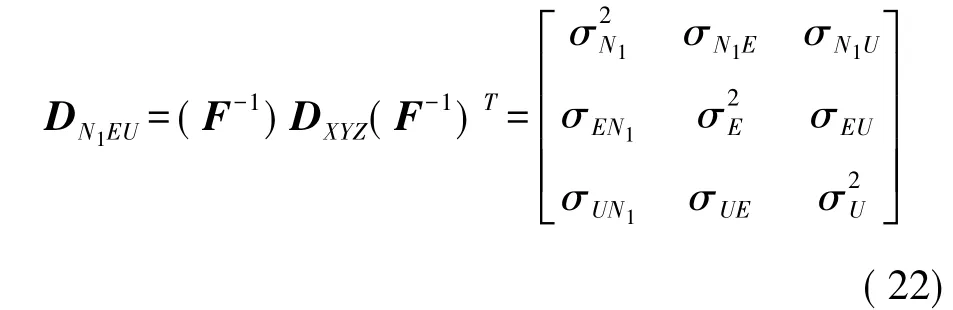
P点在大地坐标系下的点位误差可表示为［4-6］

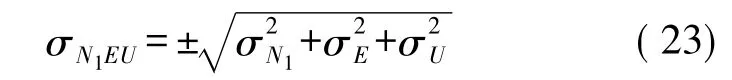
由于P点所在的子午圈、平行圈和法线方向相互垂直，则N1、E、U方向相互垂直。由于Helmert点位误差度量在二维和三维情形下具有旋转不变性，与坐标系的选择无关，即二维和三维点位方差等于任意2个和3个垂直方向的方差之和［5-6］，即理论上σN1EU=σXYZ，但各方向的方差不等。

因N1、E方向分别和x、y方向相同，若忽略P点高斯投影长度变形和大地高H(因H最大也不会超过9 km，与地球曲率半径相比为微小值)的影响，得

六、计算与分析

截取中国矿业大学CORS站点(KDJZ)的1.5 h的GNSS实测数据，采用精密单点定位模型进行解算，得到该点在WGS-84坐标系中的概略B=34°，

取最不利的情况，l=3°，H=10 000 m。

1.(X，Y，Z)误差转换为(x，y)误差

由式(14)可得

2.(X，Y，Z)误差转换为(N1，E，U)误差

由式(22)可得

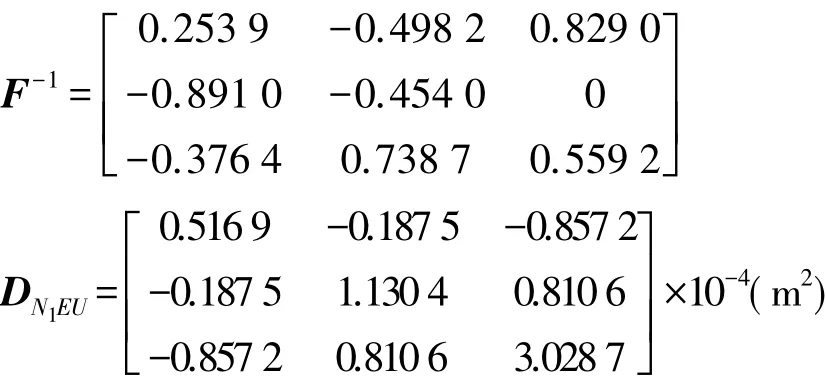
根据DXYZ、Dxy和DN1EU分别计算该点在空间直角坐标系、高斯平面直角坐标系和大地坐标系下各方向误差和点位误差，结果见表1。

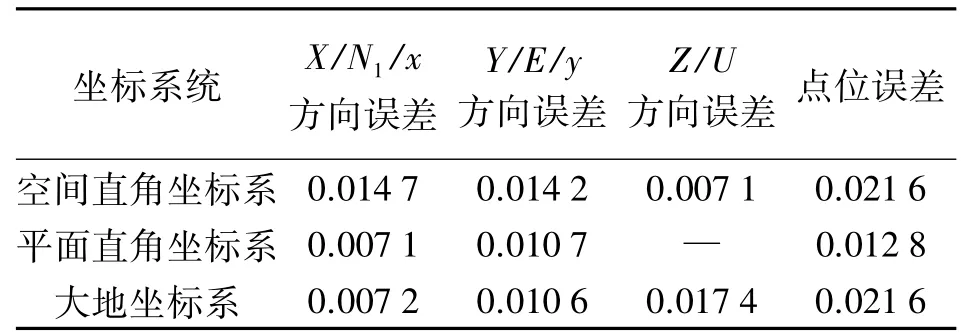
表1 3种坐标系下的误差 m

由表1可知，点位误差在空间直角坐标系和大地坐标系下其数值是相等的，但各方向的误差不相等。N1、E方向误差分别与x、y方向误差几乎相等，其微小差异是由P点高斯投影长度变形和大地高H引起的。N1、E、U方向误差更能直观地反映点位误差在3个重要方向上的大小。

3.(x，y，H)误差转换为(X，Y，Z)误差

取前面计算得到的Dxy和σ2H，组成DxyH为

由式(15)可得

4.(N1，E，U)误差转换为(X，Y，Z)误差

因 N1、E、U方向误差分别与 x、y、H方向误差相等，取

由式(20)可得

根据DxyH、DN1EU和DXYZ分别计算该点在高斯平面直角坐标系、大地坐标系和空间直角坐标系下各方向误差和点位误差，结果见表2。

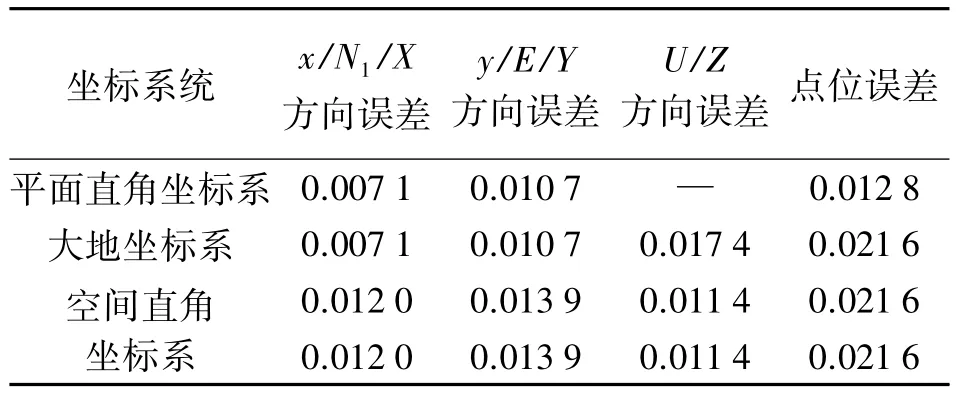
表2 3种坐标系下的误差 m

由表2可知，两种方法得到该点在空间直角坐标系下的点位误差和各方向误差都是相等的。与表1中的结果比较可知，该点在两表中的空间直角坐标系下各方向误差不相等，这是因为忽略了d x、d y和d H，以及d N1、d E和d U的相关性，因为要满足旋转不变性，其点位误差是相等的。

七、结束语

本文从大地坐标系到空间直角坐标系的全微分公式入手，推导了点位误差在两坐标系下的转换公式。结果表明，直接根据误差转换公式计算点位误差时，其转换矩阵复杂，且误差的单位不统一，不利于实际应用。而本文提出将误差单位统一用长度表示，推导的误差转换矩阵不仅形式简单，且为正交矩阵。此时，大地坐标系下3个参数的误差能直接反映平面和高程上的测量精度。

本文也从理论和算例证明，推导的大地坐标系与空间直角坐标系之间的误差转换公式，可代替现有的空间直角坐标系与高斯平面直角坐标系之间复杂的误差转换公式，其形式简单，且能满足转换精度要求。

本文的式(12)、式(13)也分别表示空间直角坐标系与文献［10］新型大地坐标系之间的全微分和误差转换公式。

［1］李征航，黄劲松.GPS测量与数据处理［M］.武汉：武汉大学出版社，2005.

［2］宁津生，刘经南，陈俊勇，等.现代大地测量理论与技术［M］.武汉：武汉大学出版社，2006.

［3］孔祥元，郭际明，刘宗泉.大地测量学基础［M］.武汉：武汉大学出版社，2010.

［4］张书毕.测量平差［M］.徐州：中国矿业大学出版社，2008.

［5］蔡剑红.一种新的点位误差度量［J］.测绘学报，2009，38(3)：276-279.

［6］杨元喜.关于“新的点位误差度量”的讨论［J］.测绘学报，2009，38(3)：280-282.

［7］赵长胜，乔仰文.空间直角坐标向高斯平面坐标转换时精度转换公式及其应用［J］.阜新矿业学院学报：自然科学版，1996，15(3)：299-302.

［8］孙小荣，徐爱功，张书毕，等.平面直角坐标与空间直角坐标间的协方差转换［J］.测绘通报，2012(3)：53-55.

［9］卞和方，张书毕，张秋昭，等.在常用坐标系下 GNSS点位误差转换方法研究［J］.大地测量与地球动力学，2012，32(4)：83-86.

［10］施一民.采用新型大地坐标系进行地形变分析的探索［J］.大地测量与地球动力学，2007，27(1)：65-68.

［11］孔祥元，郭际明.控制测量学(下)［M］.武汉：武汉大学出版社，2006.