关于测量结果不确定度表示方法的探讨

焦洋，王超，东方

(国防科技工业2311 二级计量站，黑龙江 哈尔滨150046)

0 引言

测量不确定度与测量结果相关，是定量的表征测量结果分散性的参数。测量不确定度直接反应的是测量值的分散性，是测量结果质量的衡量标准，从另一个侧面，也间接反应了被校准仪器设备的技术性能。测量不确定度一般用扩展不确定度来表示，可以采用绝对形式，也可采用相对形式。但在实际工作中采用何种形式来表示测量不确定度，有效位数如何选取，如何修约，仍存在一定的误区与争议，本文将通过实例的方式对测量不确定度的表示方法进行探讨。

1 测量不确定度的表示形式

测量不确定度的表示方法一般应与仪器设备主要技术指标的表示方法一致。当仪器设备的主要技术指标(如最大允许误差)采用相对误差形式表示的情况下，测量不确定度应采用相对扩展不确定度形式;当仪器设备的主要技术指标(如最大允许误差)采用引用误差形式表示的情况下，测量不确定度采用绝对扩展不确定度形式表示;当仪器设备的主要技术指标(如最大年稳定性)采用绝对误差加相对误差形式表示的情况下，测量不确定度采用绝对扩展不确定度的形式表示;当测量仪器的主要技术指标采用某一固定值表示的情况下，测量不确定度采用绝对扩展不确定度形式表示。测量不确定度表示方式如表1 所示。

通过上面的论述我们可以得出一个结论。仪器设备主要技术指标的表示方式可以归纳总结为2 种形式，即相对形式和绝对形式。其中，第一种形式是采用相对形式，后三种形式均可以归纳为绝对形式。

一般情况下，用相对扩展不确定度表示的测量不确定度也可以采用绝对扩展不确定度的形式进行表示，而用绝对扩展不确定表示的测量不确定度是不可以用相对形式进行表示的。因为在评定测量不确定度的过程中相对扩展不确定度是通过绝对扩展不确定度经过计算得到的。也就是说，必须先获得绝对形式的测量不确定度，才能获得相对测量不确定度。如标准测力仪测量结果的测量不确定度用相对形式进行表述(U=0.13%)，也可以用绝对扩展不确定(U =0.033 kN)来表示。而某些要用绝对形式来表示的测量不确定度，如量块的测量不确定(U =1.3 μm)就不能用相对扩展不确定度进行表示了。

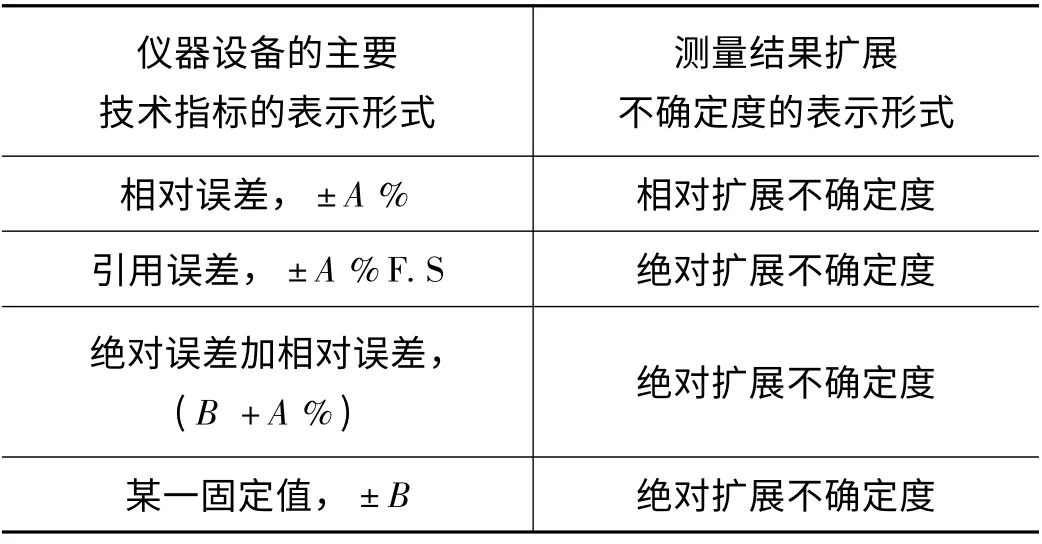
表1 测量结果不确定度的表示形式

另外，有些种类的仪器设备还采用分段形式对仪器的主要技术指标进行描述，如引伸计，在某一测量范围内采用一个固定值，在某一范围内采用相对值来反映其最大允许误差。这种情况下，测量不确定度要进行分段表示。

2 测量不确定度有效数字位数的选用及修约原则

根据JJF 1059.1 －2012 《测量不确定度评定与表示技术规范》的规定，一般情况下，测量不确定度的有效数字位数最多为2 位，包括合成不确定度、扩展不确定度以及各个标准不确定度分量。虽然，在计算过程中就对标准不确定度分量进行修约，可能会导致一定修约误差，但如果选择两位有效数字进行修约，则修约误差所带来的不确定度分量，对合成不确定度的贡献较小，一般可以做忽略处理。但为了减小数字修约所带来的影响，在计算过程中尽可能保留两位有效数字。

测量结果的测量不确定度一般以扩展不确定度的形式表示(在某些情况时以合成标准不确定度表示)，有效数字的位数为1 至2 位，并且在校准结果报告中最终报告的测量不确定度的修约位数应与测量结果的位数一致。有效数字的修约规则可以采用“不为零，即进位”的方式，如U =21.21 g，可以修约为U =22 g。但上述原则在JJF 1059.1 －2012 中不是强制规定的，也可以采用一般数字修约“四舍六入五单双”的原则。如U=21.21 g，可以修约为U=21 g。

JJF 1059.1 －2012 中规定测量不确定度位数要和测量结果的数字位数相互对齐，如某测量结果为F =(100.1 ±0.2)N(k=2)，也可以用相对不确定度表示，则为测量结果为F =100.1g，U =0.20% (k =2)。本例中用绝对形式表示的测量不确定的有效数字位数和测量结果是相互对齐的，但如果用相对形式表示测量不确定度，则测量结果的位数和相对测量不确定度转换成的绝对测量不确定度的位数，不需要对齐。下面本文将通过实例加以说明。

某仪器采用相对的最大允许误差表示其技术指标，最大允许误差为±2%，假设服从均匀分布，包含因子等于1.732，分辨力为0.1 (单位略)，采用最大允许误差为±0.1%的标准仪器进行校准，假设忽略重复性影响，测量不确定的来源仅考虑标准器和分辨力两项(u1是标准器最大允许误差引入的标准不确定度分量，u2是被测仪器分辨力引入的标准不确定度分量)，校准数据及测量不确定度的情况见表2。

从表2 可知，如果我们需要用绝对扩展不确定度的形式表示序号7 的测量结果，测量结果1000.1 和扩展不确定度1.2 的有效数字位数是对齐的。序号6、序号5 和序号4 的测量不确定度的有效位数不能和测量值相对齐，但是根据测量不确定度有效位数保留的规定，我们可以取一位有效数字，即序号6，5，4 的扩展不确定度为0.6、0.3 和0.2，修约后两者的有效数字位数可以相互对齐。序号3、序号2 和序号1 的扩展不确定度即使取一位有效数字也不能和测量结果的有效位数相对齐。

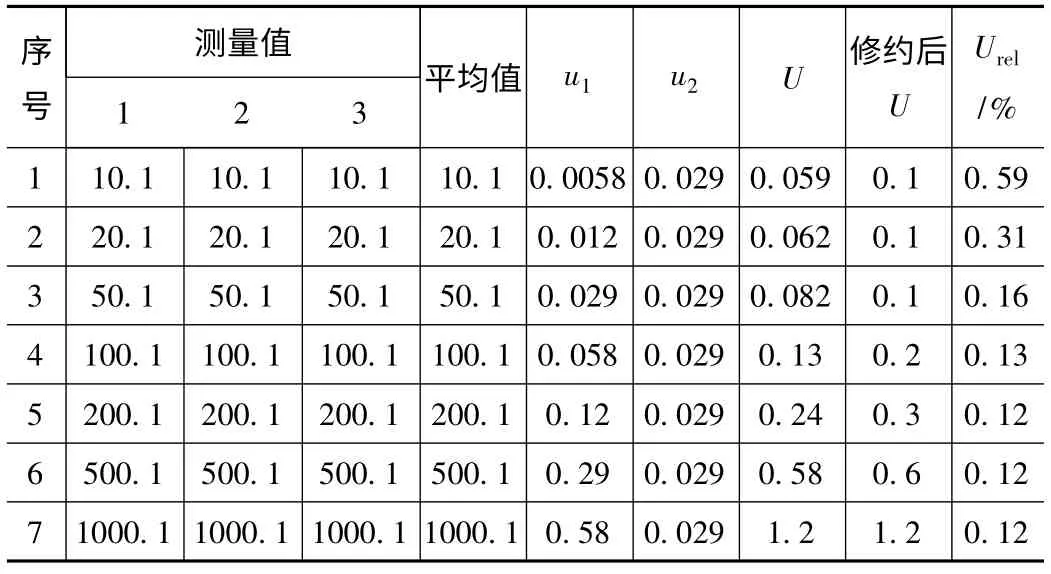
表2 校准数据及测量不确定度

以上例中的序号1 测量点进行分析，如果扩展不确定度必须采用绝度形式给出，则必须要对测量结果不确定度进行连续修约，将扩展不确定度修约至0.1，才能使测量结果和测量不确定度的位数相互对齐。虽然序号1的扩展不确定度进行了连续修约，不符合GB 8170 －2008《数值修约规则与极限数值的表示和判定国家标准》，但要符合JJF 1059.1 －2012 的要求必须如此，而且应使用“不为零，即进位”的修约原则。在日常工作中，如果遇到这种情况，我们一般采用相对形式报告测量结果的不确定度，而不采取连续修约的方式对其进行修约。

用相对形式表示的测量不确定度不存在和测量结果有效数位相对齐的限制，但值得注意的是，在用相对形式的测量不确定度时，其绝对测量不确定不能先进行数值修约，再计算，必须要使用未经数值修约的绝对扩展不确定来计算相对扩展不确定度，否则必然会大量引入由于数字修约所带来的影响因素，导致测量不确定度表示不合理。

在序号1 测量点的测量过程中，其相对扩展不确定度为0.59%。但如果选用已经修约后的绝对不确定度来计算相对扩展不确定度则为1.0%，两者相差很大，错误在于在计算相对扩展不确定度之前，对计算数据(绝对扩展不确定度)进行了连续修约所导致的。

有些错误看法认为，在用相对形式的测量不确定度的时候，其反算后的绝对测量不确定度的有效数字位数也要和测量结果的有效数位相对齐。从表2 的数据中可以看出，并不是所有的相对测量不确定度在进行反算为绝对测量不确定度后，两者的有效数字位数能够对齐，例如序号1 测量点。序号1，2，3 测量点的相对测量不确定在反算成绝对测量不确定度后不能和测量结果的有效数位对齐的根本原因在于绝对测量不确定的数值远小于测量仪器的分辨力，也就是被校准测量仪器的分度数不足所导致的现象，和相对不确定度无关。

3 结语

通过以上探讨可以总结得知，在计算测量不确定度的过程中，必须要先计算，根据实际情况选取测量不确定度的表示形式，选定表示形式后再对测量不确定度进行修约，保证绝对形式的测量不确定的有效数字位数与测量结果的位数相对齐，采用1 至2 位有效数字表示测量不确定度，注意不能进行连续数字修约。

［1］叶德培. JJF 1059.1—2012 测量不确定度评定与表示［S］.北京:中国计量出版社，2012.

［2］陈玉忠. GB/T 8170 －2008 数值修约规则与极限数值的表示和判定［S］. 中国标准出版社，2008.

［3］李宗扬. 计量技术基础［M］. 北京:原子能出版社，2002.