基于蒙特卡洛法的砝码校准不确定度评定
韩志国,李锁印,冯亚南,许晓青
(中国电子科技集团公司第十三研究所,河北 石家庄050051)
0 引言
测量是以确定量值为目的的一组操作。测量结果受人员、测量系统、测量程序、环境以及其它的因素影响而存在测量不确定度。测量不确定度是与测量结果相关联的、表征合理的、赋予被测量值分散性的参数。ISO/IEC 发布的Guide98 -3 -2008 《测量不确定度表示指南》 (GUM)给出了测量不确定度评定与表示的通用方法。2008 年,计量指南联合委员会(JCGM)在GUM 方法的基础上推出了补充件——采用蒙特卡洛法评定测量不确定度,将蒙特卡洛法作为对GUM 方法的重要补充。我国新颁布的JJF1059.2 -2012《采用蒙特卡洛法评定测量不确定度》就是依据该补充件进行编制的。该规范规定了用蒙特卡洛法评定与表示测量不确定度的方法,并就GUM 中未涉及的概率分布传播的问题提供指导,扩大了测量不确定度评定与表示的适用范围,同时该规范提供了检查GUM 法是否适用的验证方法。
1 蒙特卡洛法介绍
在测量不确定度的评定中采用的蒙特卡洛法(MCM)是一种通过重复采样实现分布传播的数值方法。与GUM 法利用线性化模型传播不确定度的解析方法不同,MCM 通过对输入量Xi的概率密度函数(PDF)离散采样,由测量模型传播输入量的分布,计算获得输出量Y 的PDF 的离散采样值,进而由输出量的离散分布数值直接获取输出量的最佳估计值、标准不确定度和包含区间。该输出量的最佳估计值、标准不确定度和包含区间等特性的计算质量随PDF 采样数增加可得到改善。
图1 描述的是,由输入量Xi(i =1,…,N)的PDF,通过模型传播,给出输出量Y 的PDF 的一个过程示意。图1 列出了分别为相互独立的正态分布、三角分布和正态分布的3 个输入量,而输出量的PDF 显示为分布不对称的情形。

图1 输入量独立时分布传播的描述
当测量模型是线性的,且输出量概率分布是正态分布时,GUM 方法可以提供准确的不确定度和包含区间。但是,如果输出量的结果是图1 所示的不对称的情形,那么采用GUM 方法进行不确定度评定时可能就会得出不切实际的包含区间,此时采用蒙特卡洛法就是有效的替代方法。由于使用蒙特卡洛法进行不确定度评定时需要对概率分布进行随机采样,因此进行不确定度评定时,应利用合适的软件进行计算 (例如MATLAB)。
2 用蒙特卡洛法评定砝码校准不确定度
虽然GUM 法在许多情况下被认为是非常适用的,但是确定是否满足其所有应用条件并不总是一件容易的事。由于MCM 的适用范围比GUM 法更广泛,建议用MCM 及GUM 法两种方法同时进行不确定度评定,并对结果进行比较,如果比较结果较好,则GUM 法适用于此场合及今后足够类似的情形,否则,应考虑采用MCM 或者其它合适的替代方法。
下面以本实验室2012 年在砝码能力验证中校准100g 砝码为例,介绍一下如何使用MCM 方法进行不确定度评定。本次校准使用的标准砝码为E2等级100g砝码,天平为TG328A 型机械天平。
2.1 建立测量模型
本次测量使用的是双次替代法,用密度为ρr的标准砝码R 对密度为ρt的砝码进行校准,两个砝码标称值相同,需要在密度为ρa的空气中进行平衡配重。通常ρt和ρr不同,因此需考虑浮力的影响,应用阿基米德定律,得到模型如下

式中:ms是密度为ρr灵敏度小砝码质量,用来测量机械天平的分度值。ΔI 为被测砝码与标准砝码标尺读数偏差;ΔIs为放上灵敏度小砝码后,标尺偏离的读数。以折算质量mct,mcr,mcs为变量,模型(1)转变为
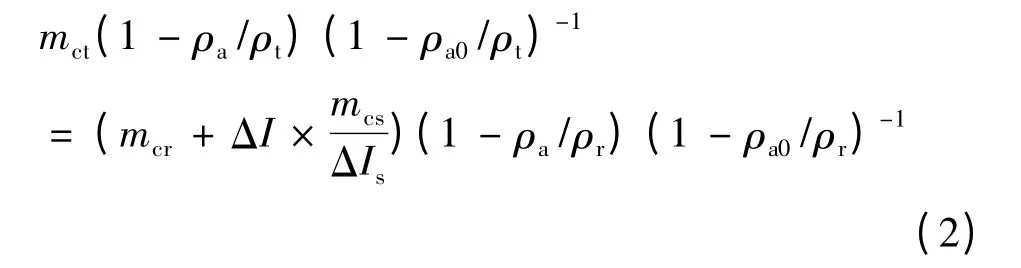
将公式(2)整理得

设Δmc= mct- mnom为mct与标称质量mnom=100 g的偏差。因此本例中使用的模型为
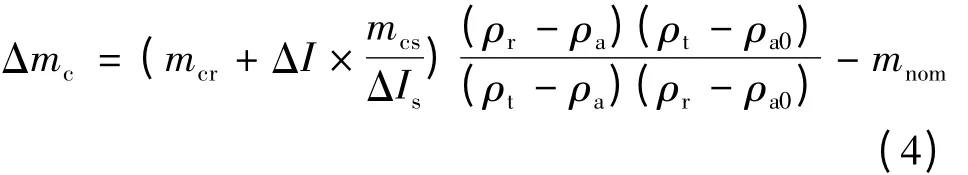
2.2 确定输入量的概率密度分布函数(PDF)
可根据一系列测量值的分析,或根据某些历史数据、校准数据和专家判断之类的信息所得到的科学判断,为各输入量设定PDF。各输入量服从的分布、最佳估计值以及标准不确定度均列入表1。其中ρa0=1.2 kg/m3,是约定空气密度,不包含不确定度。

表1 关于质量校准模型的输入量及其概率密度函数
表1 中,标准砝码的相关信息是通过检定证书和JJG99 -2006 《砝码检定规程》得到。ΔI 与ΔIs的相关信息是通过使用双次替代法重复测量10 次得到。砝码的密度信息是通过JJG99 -2006 《砝码检定规程》中给出的典型材料密度表中查表得到。空气密度ρa的信息是由JJG99 -2006 《砝码检定规程》中得到。
2.3 蒙特卡洛试验次数
在规定的数值容差下MCM 所提供的结果所需的试验次数跟输出量的PDF “形状”及包含概率有关,应合理选择蒙特卡洛试验次数及样本量的大小M,一般情况下取M=106,这样通常会为输出量提供95%包含区间,该包含区间长度被修约为1 或2 位有效十进制数字。
2.4 程序
本程序是使用MATLAB 进行编制的,具体如下:
clc;clear; %清除MATLAB 中的变量。
M=1000000; %设定蒙特卡洛试验次数。
m0 =100; %砝码标称质量(单位:g)。
dr=0.04; %标准砝码折算质量修正值(单位:mg)。
ur=0.033; %标准砝码不确定度(单位:mg)。
mr=normrnd ((m0* 10^3 +dr),ur,1,M); %标准砝码采样值(单位:mg)。
ms=normrnd (10,0.002,1,M); %灵敏度小砝码采样值(单位:mg)。
dI= normrnd (4.2,0.2,1,M); % 读数重复性 (单位:格)。
dIs = normrnd (99.6,0.3,1,M); % 灵敏度读数重复性(单位:格)。
rou0 =normrnd (8,0.07,1,M); %标准砝码材料密度(g/cm3)。
rou1 =normrnd (8,0.07,1,M); %被检砝码材料密度(g/cm3)。
ra=0.24* rand (1,M) +1.08; %空气密度(mg/cm3)。
r0 =1.2; %标准空气密度(mg/cm3)。
dm= (mr+dI.* ms. /dIs). * (rou0* 10^3 -ra). * (rou1*10^3 -r0). / ((rou1* 10^3 -ra).* (rou0* 10^3 -r0)) -m0
* 10^3;%双次交换衡量法数学模型。
s=std (dm); %输出量标准不确定度。
avg=mean (dm); %输出量估计值。
y=sort (dm); %将试验结果从小到大进行排列。
y_ low=prctile (y,2.5); %包含概率为95%时,包含区间的下限值。
y_ high=prctile (y,97.5); %包含概率为95%时,包含区间的上限值。
2.5 报告结果
MATLAB 程序运行得到如下结果:
被校砝码折算质量偏差为0.46 mg;标准不确定度为0.04 mg;包含概率为95%;包含区间为[0.38 mg,0.54 mg]。图2 给出了上述程序得到的输出量的近似概率分布。图中,柱状图是输出量的近似概率分布,实线是正态分布曲线,可见输出量近似服从正态分布。

图2 输出量近似概率分布
3 蒙特卡洛法与其它不确定度评定方法的比较
3.1 GUM 法评定砝码校准不确定度
由于使用偏导的解析计算对公式(4)求偏导过于复杂,因此将公式(4)作近似处理,得

对上述模型求偏导,得到各输入量灵敏系数如下:
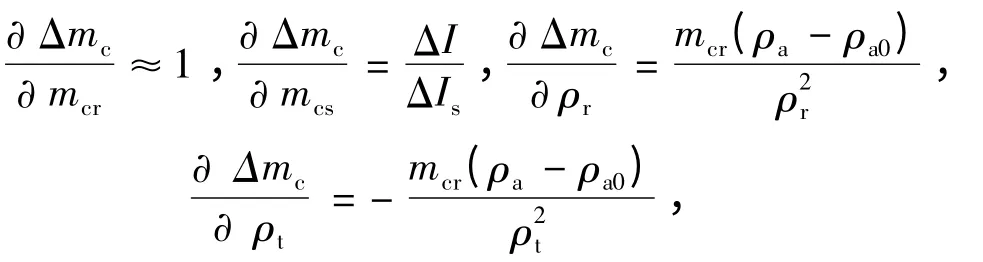
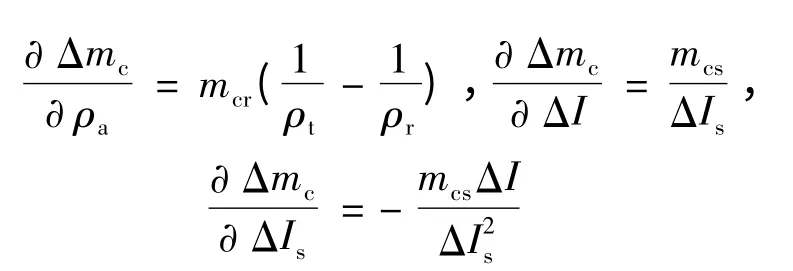
则合成标准不确定度为

将表1 中输入量的相关信息带入上式,计算得uc=0.04mg,取包含概率为95%,得到如下结果:
被校砝码折算质量偏差为0.46 mg;标准不确定度为0.04 mg;包含概率为95%;包含区间为[0.38 mg,0.54 mg]。
3.2 JJG99 -2006 《砝码检定规程》中的方法评定砝码校准不确定度
规程中认为砝码的校准不确定度由以下几个方面引入:衡量过程,标准砝码,空气浮力修正,天平。各不确定度分量列入表2。

表2 测量不确定度分量一览表
取包含概率为95%,得到如下结果:
被校砝码折算质量偏差为0.46 mg;标准不确定度为0.05 mg;包含概率为95%;包含区间为[0.36 mg,0.56 mg]。
三种方法得到的结果见表3。

表3 砝码校准计算结果
由三种方法得到的比较结果可知,MCM 与GUM得到的结果一致,而规程给出的不确定度略显保守。这主要是由于某些不确定度分量被重复计入和计量人员对不确定度分量的不同理解程度而造成的。按照JJF1059.2 -2012 《用蒙特卡洛法评定测量不确定度》中使用MCM 验证GUM 的要求,GUM 法通过了验证,在以后进行砝码校准不确定度评定时,可以使用GUM法进行评定。
4 结论
MCM 尤其适用于以下两种情况:不宜对测量模型进行线性化等近似的场合,在这种情况下,按GUM 确定输出量的估计值和标准不确定度可能会变得不可靠;输出量的概率密度函数较大程度地偏离正态分布或t 分布,例如分布明显不对称的场合,在这种情况下,可能会导致对包含区间或扩展不确定度的估计不切实际。另外,如果GUM 法通过了MCM 的验证,即GUM 法若明显适用,则GUM 法依然是不确定度评定的主要方法。在实际工作中可以根据实际情况选用合适的方法进行测量不确定度的评定。
[1]国家质量监督检验检疫总局.JJF1059.2 -2012 用蒙特卡洛法评定测量不确定度[S]. 北京:中国计量出版社,2012.
[2]Evaluation of measurement data — Supplement 1 to the“Guide to the expression of uncertainty in measurement”— Propagation of distributions using aMonte Carlo method [S]. ISO/IEC,2008.
[3]国家质量监督检验检疫总局.JJG99 -2006 砝码检定规程[S]. 北京:中国计量出版社,2006.
[4]陈怀艳,曹芸,韩洁. 基于蒙特卡罗法的测量不确定度评定[J]. 电子测量与仪器学报,2007,25.
[5]倪育才. 实用测量不确定度评定[M]. 北京:中国计量出版社,2010.

