定容过程气体水合物相平衡计算研究①

陈 鹏 李玉星 王武昌 刘海红 张庆东

（中国石油大学（华东）储运与建筑工程学院）

传统的四相闪蒸计算如图1所示，考虑相平衡之后的气相、液态烃相、水相以及水合物相四相，计算过程以相平衡前的初始条件为计算起点，不断修正气相摩尔分数，最终达到计算平衡。而在本文计算过程中，考虑到水合物浆制备的两种反应过程：定容反应和定压反应，如图2所示，并且以相平衡终点为依据：气相过量或者液相过量，划分计算过程并计算相平衡参数。

1 模型建立与分析

定压过程的相平衡计算过程在Chen－Guo模型［1－2］中已有详细的讨论，在此不再赘述。文中所讨论的定容反应，是指在体系内充入反应气体至一定压力值后，关闭入气口阀门，待反应达到相平衡为止，因反应过程中体系压力不断降低而体系总容积维持不变，因此一般称此过程为定容反应过程。

1.1 模型建立

对于定容反应过程，随着水合物的形成，气体、液体不断消耗，体系压力随之降低，在气相过量时，水可以全部转化为水合物，此时体系中只有气相、水合物相；在液相过量时，最终的平衡压力稳定在气相的相平衡压力，此时体系中有平衡气相、水合物相以及液相。

通过上述分析，对水合物浆定容条件制备过程提出如下假设：

（1）忽略溶解的气体对水合物生成过程的影响。

（2）在气相过量时，近似认为水可以完全转化为水合物。

据此，建立定容过程水合物生成相平衡的计算方法，通过不断减小气相的转化因子e，计算反应消耗的气量、水量W以及平衡压力p，并通过对比消耗水量W与体系总水量Vw以及平衡压力p与水合物生成压力pH的大小，判断反应的终止时刻。据此，计算反应终止时，体系的状态及相关参数。

1.2 计算方法

计算框图如图3所示。

式中：T为体系温度；p0为初始充气压力；Zi为体系气相组分摩尔分数；V为反应体积总容积；Vw为水相体积；p为当前计算得到的平衡压力；pH为计算得到的水合物生成压力；yi为修正后的体系气相组分摩尔分数；W为反应消耗的液相总量；e为转化因子，e＝V／F，为平衡气相和初始气相的摩尔数之比；K为计算步数。

详细计算过程如下所示：

（1）根据体系初始参数，结合亨利定律，计算溶解平衡压力ps和溶解平衡气相摩尔数Ng。

亨利定律表达式如下：

式中：H为亨利系数；Xi为气体组分i的摩尔溶解度；pi为气体组分i的分压。

第3种情况Wλ=1，WMAC=0.2，wp=1，在上一种情况的基础上加入了对修正参数变化量的限制，即式(7)的模型修正问题。

（2）给定初始转化分率e＝1，根据e以及上步循环计算得到的压缩因子Z，结合状态方程，计算体系压力p′，进而得到气体组分i的逸度fi、气体组分在水合物小孔中的占有率θi，以及占水合物中气相的摩尔分数Xi。

式中：fi为气体i的逸度；Cij为气体i对应j型结构的Langmuir常数。

式中：αT为和水合物构型相关的系数；X＊i，j为气体在水合物大孔中的占有率。

（3）根据e以及Xi，重新计算体系气相的气体组成及摩尔分数yi。

（4）根据e以及θi，计算水合系数n，结合e，得到消耗水量W。

水合系数可以根据下式计算［3］：

结构I型水合物：

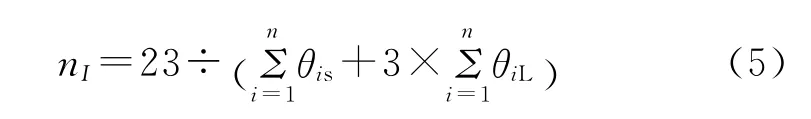
结构II型水合物：

消耗水量计算式为：

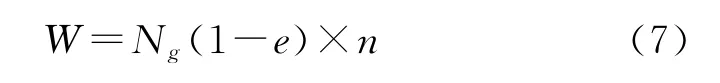
式中：Ng为体系达到溶解平衡时的气相摩尔数；θiS为气体组分i在水合物小孔中的填充率；θiL气体组分i在水合物大孔中的填充率。

（5）根据计算得到的yi，应用 Chen－Guo模型计算此时水合物的生成压力pH，在此不再赘述。

（6）对比此时消耗水量W与Vw，以及此时体系压力p′与水合物的生成压力pH。

（7）假如W＞＝Vw或p′＜＝pH，则反应终止，否则，e＝e－0.001，重复计算（2）～（5）步。

（8）根据上步计算所得到的结果，进一步计算处理，即可得到：气相平衡压力、体积，水合物相摩尔数、体积、密度、气体组成，以及水相体积、水合物浆液的体积浓度以及浆液黏度计算值。

据此，对上述程序编制应用界面如图4所示。

通过以上过程，可以对任一体系，在给定气相组成、温度、初始压力的条件下，计算反应相平衡时的体系状态参数，包括气相压力和体积，水合物相体积、密度、组成，水相的体积、浆液的体积浓度以及应用Thomas模型等对浆液黏度做出的预测。在此基础上，设计出实验方案，对预测结果和实验结果进行了对比。

2 实验设计及结果对比

采取改变充水体积的方式，对不同相平衡状态进行实验结果与预测结果的对比，实验方案如表1所示。

实验结果与计算结果对比如表2所示。

表1 定容过程对比实验方案及结果Table 1 Experiment scheme and results of constant volume process

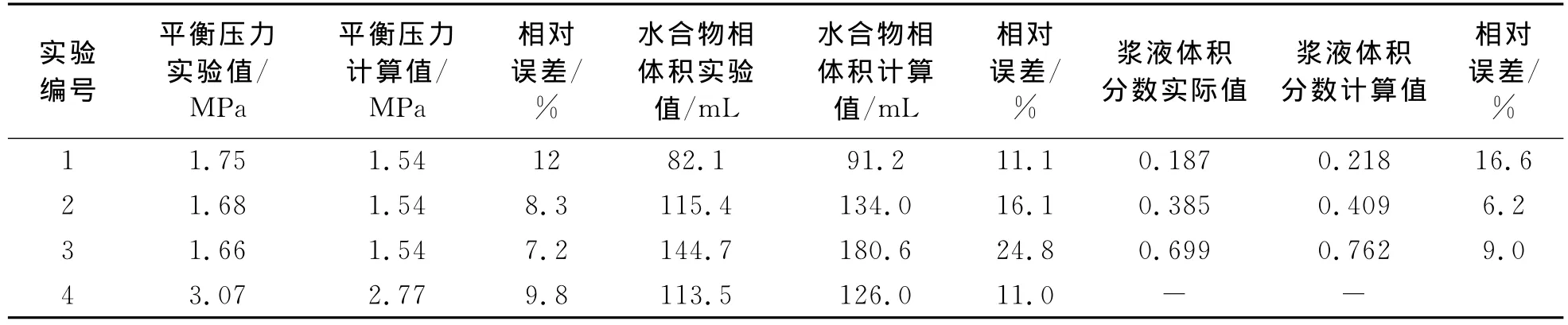
表2 实验结果处理与对比Table 2 Process and comparison of experimental data

通过以上工作，可以得到如下结论：

（1）上述模型可以对定容条件下，水合物制备过程相平衡参数进行良好的预测。

（2）模型对反应平衡压力、浆液体积分数的预测误差在10%以内，误差来源主要包括CO2的溶解、实验中不可避免的操作误差以及模型中的近似化处理等。

（3）模型对液相体积较低情况时的预测结果误差较大，主要是因为在液相体积较低时，水合物生成过程缓慢，需要达到相平衡的时间较长而实验条件并不允许所造成的。

（4）通过对比实测黏度与计算黏度值，可以发现Thomas模型可以对较低浓度下水合物浆液的黏度给出较为准确的结果，但是在较高浓度下，尤其是浆液体积分数超过了最大填充率之后，预测结果明显偏大。

（5）对于模型给出的其他计算结果，由于缺乏有效的实验数据，无法一一做出比较分析，还需完善实验手段，对模型计算结果进行进一步验证。

3 结论

通过对实验过程的分析，对水合物浆相平衡计算过程进行了有效简化，所提出的计算模型可以对任一初始条件下的体系相平衡状态进行准确预测，预测结果包括平衡时各相的状态参数以及所形成水合物浆的物性参数等。实验证明，该模型不仅对水合物浆制备过程预测具有重要意义，而且为进一步研究水合物浆流动状态做了铺垫。

［1］陈光进，孙长宇，马庆兰.气体水合物科学与技术［M］.北京：化学工业出版社，2007：56－83.

［2］孙志高，石磊，樊栓狮，等.气体水合物相平衡测定方法研究［J］.石油与天然气化工，2001，30（4）：164－166.

［3］陈多福，徐文新，赵振华.天然气水合物的晶体结构及水合系数和比重［J］.矿物学报，2001，21（2）：159－164.