双振动体惯性往复反共振振动筛的动力学分析

方守艳，胡继云，孙庆春

（河南工业大学 机电工程学院，河南 郑州 450001）

0 前言

惯性往复振动筛作为一种重要的筛分机械，被广泛应用在粮食的清理和筛分等方面.传统的惯性往复振动筛有两种形式即共振式和远超共振式.其振动电机均安装在振动体筛箱上，这不仅导致了参振质量和激振力的增加，还使振动电机的寿命减少.除此之外筛箱的侧板容易产生破损，振动噪声也较大，这对生产人员的健康不利等[1-3].针对传统惯性往复振动筛的缺点，作者基于反共振理论，设计出一种新型的反共振振动筛.

对于多自由度振动系统，当激振频率达到一定值时，其中一个自由度的振动静止，这种现象叫反共振现象[4].目前许多学者和技术人员对反共振理论的发展和应用做了大量的研究工作，并设计出一些反共振机械，但在粮机方面的反共振机械则极为稀少，因此，作者对惯性往复反共振振动筛的研究具有一定的理论意义和应用价值.

图1 力学模型

1 力学模型（图1）及动力学方程求解

图1中上振动体m2是振动筛的工作部分，下振动体m1是振动筛的支撑架.k1、k1x是下支撑弹簧在铅垂和水平方向上的刚度，c1、c1x是其阻尼.k2、k2x分别是上支撑弹簧在铅垂和水平上的刚度，c2、c2x是其阻尼.m0是偏重块的质量，激振力则为F sin wt，力幅F=2m0rw2[5-6].主要以铅垂方向为重点，进行动力学参数分析.根据牛顿第二定律，建立系统在铅垂方向上的动力学微分方程为：

利用复数法对式（1）进行求解，设受迫振动的稳态复数解为：

为了更加直观地分析各个参数对振幅值的影响，需要对其进行简化，式中将引入的变量为：

2 动力学参数分析

由式（8）、（9）可以看出参数 α、u、λ、ξ1、ξ2等对系统振幅的大小及稳定性均有一定的影响，因此合理选择这些参数则显得尤为重要[7].根据实际工程和机械设计原理可知，在上、下振动体设计完成之后质量即可确定，而阻尼是材料的固有属性，在弹簧选定之后即可确定，因此 ξ1、ξ2、m1、m2对于振动机械来说可看作已知参数，研究中其数值分别为 0.1，0.007，100 kg，300 kg. 在此不再具体分析其对上、下振动体幅频特性曲线的影响.接下来的分析则为计算k1、k2的值做准备.

图2 α=1时上、下振动体的幅频特性曲线

图3 α=2时上、下振动体的幅频特性曲线

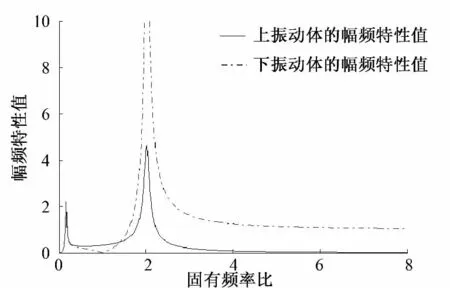
图4 α=3时上、下振动体的幅频特性曲线

由图2—图4可以看出：

（1）当λ=1时下振动体的幅频特性曲线趋近于零，而上振动体的幅频特性曲线有一定的数值，这种现象即为反共振现象.所以，为了减少满足工作振幅所需的激振力和传给基础的动载荷，本设计选择反共振点作为工作点，λ=1时的点即为反共振点.

（2）当上、下振动体的固有频率比α值增大时，在反共振点或者附近的幅频特性曲线越来越平缓，这也意味着负载、振动电机电网、物料变化等外界因素引起的频率比的变化对系统振动特性的影响越来越不明显.此外，系统在启动停车时经过共振区的瞬态振幅也在逐渐减小，这表明此时传给基础的瞬态载荷在减小.基于这两点，α值越大越好.但α越大也就意味着k1越小，为了保证下振动体支撑弹簧的刚度，一般应使α≥2.

3 算例

根据分析，对提到的反共振振动筛的机构动力学参数仅有k2的值是未知的，为了确定k2值，就要先确定α的值.选取不同的α值和λ的值在0.8～1.3之间波动时，系统的各个动力学参数值如表1—表3所示，其中，β1=（A1m1）/（2m0r）；β2=（A2m2）/（2m0r）.

表1 α=2时的动力学参数值

表2 α=3时的动力学参数值

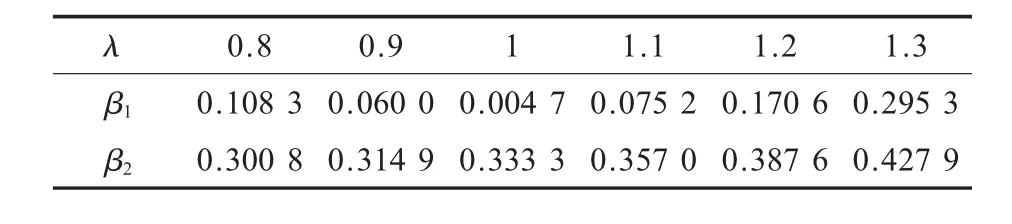
表3 α=4时的动力学参数值

由表1—表3可以看出：系统工作在反共振点时，α=3下振动体的振幅最小.此外还可以看出此时上振动体在反共振点附近的幅频特性曲线值变化小，这就意味α=3时，系统工作时的稳定性较好.所以，根据工程实际，对于此类振动机械的设计推荐α=3.

4 结论

建立了双振动体惯性往复反共振振动筛的力学模型，对其进行动力学分析，依据分析结果得出以下结论：

（1）当λ=1时，出现反共振现象，此时上振动体的振幅较大，而下振动体的振幅趋近于零，从而验证了反共振理论在本设计中应用的可行性.此时上振动体的刚度可根据公式k2=w2m2求得.

（2）在保证下振动体支撑弹簧刚度和上振动体工作振幅的前提下，α越大越好.α越大，系统的两个共振点的间隔越大，系统的振动特性对频率变化的灵敏度越低.下振动体的刚度可根据k1=求得.

［1］ 季文美，方同，陈松淇．机械振动［M］.北京：科学技术出版社，1985：48-51.

［2］ 王正浩.振动筛的研究现状与发展趋势［J］.沈阳建筑工程学院学报，1999，15：78-80.

［3］ 侯书军.双质体线性振动系统的动力学研究［J］.河北科技大学学报，2003，24：1-4.

［4］ 韩运侠.反共振现象及其应用［J］.洛阳师专学报，1998，17:48-50.

［5］ 闻邦椿，刘树英.振动机械的理论与动态设计方法［M］.北京：机械工业出版社，2001.

［6］ 胡继云，雷飞，秦玉良．惯性往复振动机械阻尼值设计的理论研究［J］．河南工业大学学报：自然科学版，2010，31：19-24.

［7］ 胡继云，廉振红，邵洪涛．惯性往复振动机械支承刚度和偏重参数的设计［J］．河南工业大学学报：自然科学版，2008，29：92-95.