智能开关用新一代永磁机构的研制
杨文选,樊恩红,家文杰
(运城供电公司,山西 运城 044000)
0 引言
近年来,永磁机构在真空断路器中的应用越来越多,它将电磁机构与永久磁铁有机地结合起来,利用永磁保持,而不需要任何电能。永磁机构结构简单,零部件很少,机械寿命长。对于断路器而言,灭弧室触头的运动速度、操动机构动作的可靠性是衡量一台断路器性能好坏的重要标志。研究永磁机构的动态特性对合理设计机构、优化机构以及机构结构的改进都具有重要的理论和现实意义[1]。
本文在永磁机构动态、静态特性分析的基础上,以12 kV户外智能开关配永磁机构为例,利用有限元法进行建模仿真,通过大量的试验研究,得出永磁机构以及智能开关较优越的机械特性,旨在提高永磁机构以及开关的机械特性。
1 永磁机构设计
本文设计的永磁机构采用小型化设计原则,整体结构如图1所示。其中导磁端盖采用阶梯式设计,缩短了永磁体的磁路,进而改善机构的磁场分布,提高机构的静态保持力。另外,缩短磁轭高度并增加导磁回路截面积,这种设计不仅缩短机构的整体长度和磁力线路径,还增加磁力线密度,使其磁场分布更加合理,从而增加机构合闸出力。

图1 永磁操动机构结构图
2 永磁机构动态特性的数学模型
采用充电电容放电的励磁方式,为分、合闸操作提供电流的电路简图如图2所示,图中C为充电电容,R和L分别为线圈的等效电阻和等效电感。
其满足的电路方程式为


图2 充电电容放电励磁方式电路简图
式(1) 中,uc为充电电容初始电压,V;i为线圈中分闸或合闸电流,A;i=-,其中C为充电电容容量,F;R为线圈的等效电阻,Ω;Ψ为电磁系统的总磁链,单位为Wb,是电流i和动铁芯位移x的函数,即Ψ =f(i,x)。
单稳态永磁机构中的磁场、位移等都处于变化之中,它求解的是一个电、磁和机械的耦合场问题。本文在建立永磁机构动态特性求解数学模型的基础上,同时求解电路方程、电磁场方程和运动方程来研究单稳态永磁机构的动态特性。对于本文所研究的单稳态永磁机构来说,其动态特性满足公式(2) 所示的微分方程组。
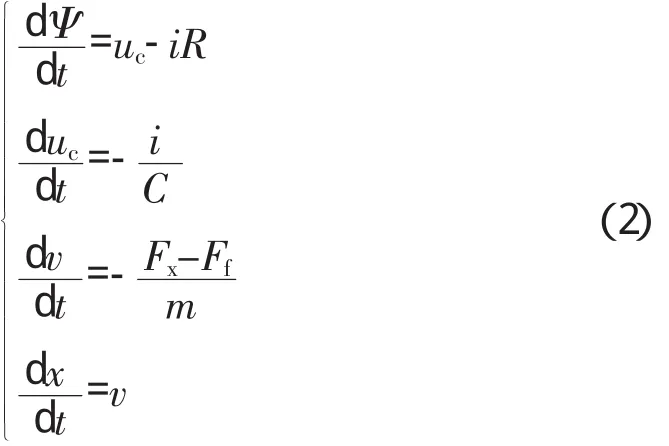
式(2)中,v为动铁芯的运动速度;m为系统运动部件归算到动铁芯处的等效质量,kg;Fx为动铁芯受到的电磁吸力,N;Ff为动铁芯的运动反力,N;x为动铁芯的位移,m。各变量的初始条件为Ψ|t=0,uc|t=0=uc0,v|t=0=v0=0,x|t=0=x0=0,求解方程组,即可得到永磁机构的动态特性。
3 质量归算与反力计算
3.1 质量归算
在进行永磁操动机构动态特性分析时,需将系统运动部件的质量归算到计算点处。如图3为单稳态永磁机构真空断路器动态计算简化模型,其中M1代表三相灭弧室侧运动部件的总质量,M2代表机构侧运动部件的总质量,AB和CD分别为断路器处于分闸位置和合闸位置时连接拉板的位置,α和β分别为分闸和合闸位置连接拉板与水平方向的角度。

图3 断路器动态特性计算简化模型
三相灭弧室侧质量M1由动触头、导电夹、软连接、绝缘拉杆、触头弹簧等构成,大小为6.6kg,由于三相灭弧室侧各运动部件做垂直运动,因此可将其替代质量集中在B点。机构侧质量M2由动铁芯、主轴、分闸弹簧等构成,大小为7.5 kg,由于机构侧各运动部件做水平运动,因此可将其替代质量集中在A点。连接拉板质量M3总质量为0.3 kg,连接拉板一端做水平运动,一端做垂直运动,因此本文在计算过程中,将其替代质量M3/2集中于A点,M3/2集中于B点。因此节点A和B上的节点质量分别为MA=M2+M3/2=7.65 kg,MB=M1+M3/2=6.7 kg。本文以动铁芯(A点) 作为计算点,根据能量平衡原理,求出整个系统的等效质量M。

式 (3) 中,vA为节点A的运动速度,m/s;vB为节点B的运动速度,m/s。
从式(3) 可以看出,求等效质量M需先求出节点A和B的速度比vA/vB,由于本文的传动机构比较简单,因此在计算速度比vA/vB时,采用图解法[2]进行求解,如图4所示。计算点A在水平方向上做平移运动,水平线段OA代表vA,B点对A点的相对速度vBA的方向与连接拉板AB垂直,从A点做直线AA′与连接拉板AB的方向垂直,直线AA′与OB′交于B点,由于vA+vBA=vB,因此线段OB即代表运动速度vB。经过计算可得

可见,该速度比并非一个定值,与连接拉板和水平方向的角度α的大小有关,将式(4) 代入式(3) 中可得

由式(5) 可知,等效质量M在整个运动过程中不是常数,是随角度α的改变而改变。

图4 图解法求速度比
3.2 反力归算
真空断路器的动作过程中运动部件的运动方向既有竖直方向又有水平方向,而且力的作用点也不同,如触头反力、触头弹簧力都作用在动触头上,而分闸弹簧力作用于动铁芯上。因此在进行动态特性计算时需要进行力的归算[3],将所有的反力归算到计算点——动铁芯上。
4 永磁机构有限元模型
目前求解电磁场的方法很多,如解析法、图解法、模拟法和数值解法。前三种方法的应用范围具有较大的局限性,数值解法近年来得到了广泛应用。比较常用的数值解法有差分法和有限元法,本文在求解过程中采用有限元法进行求解。有限元法的基本思想是把复杂的结构或场(空间)看成由有限个单元组成的整体。首先把一个实际具有无限个节点连续介质的结构或场(空间)通过网格剖分,离散成有限个节点连接起来的有限个单元来进行分析,在单元分析的基础上,将所有单元综合起来进行总体合成,建立整个系统的联立方程组,借助于电子计算机求得连续整体的近似解。
使用有限元仿真软件对永磁机构进行特性仿真时,首先建立机构模型,对各个元件的材料赋予属性,永磁体材料设计为NdFe35,磁轭材料设计为steel-1008。
本文针对模型结构进行剖分,剖分网格是采用手动剖分,计算模型和剖分图如图5所示。由于永磁机构为轴对称结构,图中采取实体剖分与表面剖分相结合的方法进行网格划分[4]。由图中可以看出,导磁部分与气隙的网格划分很密集,非导磁部分与边界网格密度相对较小。

图5 永磁机构计算模型与剖分图
5 永磁机构动态过程仿真分析
合理设计永磁机构线圈结构并赋予电源后运行程序,动铁芯由分闸位置向合闸位置运动。通入电流后,机构上端的磁力线明显增多。随着电流的逐渐增大,动铁芯受到的电磁吸力越来越大,位移也逐渐增大,上部气隙磁阻逐渐减小,下部气隙磁阻逐渐增大,因此机构上部的磁场逐渐增强,绝大部分的磁力线经由上部气隙、上端盖、机构外筒、永磁体和磁套形成闭合磁路。随着动铁芯电磁吸力的逐渐增大,动铁芯不断地向合闸方向运动,直到运动到合闸位置为止,动铁芯已保持在合闸位置,此时机构内的磁场为永磁体单独作用产生的,至此机构就完成了整个合闸过程。
对永磁机构线圈赋予反相电源并串入11Ω分闸限流电阻后,运行程序即可完成分闸过程。线圈分闸电流产生的磁通与永磁体的磁通方向相反,磁通经抵消后永磁机构在分闸反力的作用下实现分闸。
6 结果及分析
图6—图8为永磁机构分合闸电流、行程随时间变化的仿真曲线和试验曲线,图中仿真曲线为ansoft有限元软件仿真得到的电流、行程曲线,试验曲线为试验研究过程中,由记忆示波器测得的电压信号经转换后得到电流曲线和机械测试仪测得的行程曲线。电阻分压器转化变比为6 A/100 mV。
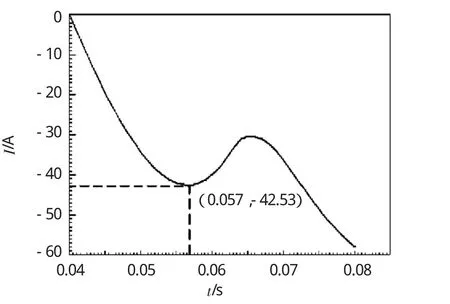
图6 机构合闸电流仿真曲线

图7 机构合闸行程仿真曲线

图8 断路器合闸行程实测曲线
从图6中可以看出,仿真计算的线圈合闸电流峰值为42.5 A,从图7中可以看出,机构合闸时间为23 ms;而从示波器实测的电压为680 mV,可算得实测线圈合闸电流大小为40.8 A;从图8中可以计算出机构及开关的合闸速度,即触头闭合前6 mm内的平均速度为1.07 m/s,全程平均速度为0.78 m/s。可以看出机构的合闸特性优异,且实际试验值与理论计算误差符合设计要求,充分验证该动态计算方法的正确性。
从图9可以看出,仿真计算的线圈分闸电流峰值为4.95 A;从图10中可以看出,机构分闸时间为17 ms;而从示波器实测的电压为108 mV,可算得实测线圈分闸电流大小为6.4 A;从图11中可以计算出机构及开关的分闸速度,即触头分开后6 mm内的平均速度为1.16 m/s,全程平均速度为1.22 m/s。此外,在其分闸行程曲线中还测得机构的开距为9.3 mm,超程为3.3 mm,过冲为1.86 mm,分闸弹跳为0.2 mm。可以看出机构的分合闸特性非常优异,完全满足断路器开断特性的要求,且实测值与理论值也符合设计误差要求。

图9 机构分闸电流仿真曲线

图10 机构分闸行程仿真曲线

图11 断路器分闸行程实测曲线
验证结果表明仿真结果与试验结果具有很好的一致性,证明使用有限元法分析机构动态特性的正确性和可行性,利用该方法可真实地反映出本文所研究智能开关配用的单稳态永磁机构的动态特性。
7 结语
通过求解电、磁、机械耦合场可获得永磁机构的动态特性,结果表明仿真值和实测值具有较好的一致性,说明本文所建立的永磁机构动态特性计算模型能够较准确地计算实际系统的动态特性。同时,本文设计永磁机构应用于INT2000型智能开关中,该开关的分合闸速度等机械特性完全符合技术要求,可以为以后大容量的真空断路器配永磁机构提供设计参考。
[1] 林莘.永磁机构与真空断路器[M].北京:机械工业出版社,2002.
[2] 高会军,林莘,蔡志远.永磁操动机构磁场计算及动特性分析[J].沈阳工业大学学报,2000,22(4):490-493.
[3] 盛剑霓.工程电磁场数值分析[M].北京:机械工业出版社,2003.
[4] 尹华杰,金振荣.有限元方法中永磁励磁的自动处理[J].微特电机,1993(4):9-10.

