加权条件风险价值下的最优购电组合研究

蒙万兴，李 将，李 力

（1.长沙理工大学电气与信息工程学院，湖南 长沙 410004；2.阳泉市供电公司，山西 阳泉 045011）

0 引言

关于购电分配和风险管理问题方面，以往考虑供电公司在不同的市场中，如长期合同市场、现货市场和自备电厂间的电量分配问题，都没有把需求反应、用户的互动考虑在内，而本文另外把用户端主动参与备用市场服务也包括进来，以方便电力公司通过需求侧的参与，达到自身利益的最大化、风险最小化，同时也使得系统更加安全稳定运行。

在电力市场环境下，电力公司承受的风险主要包括以下几个方面：价格风险，容量风险，信贷风险，政策风险等。到目前为止，主要有三种量化风险的方法，即：概率方法，模糊集方法和遗憾值方法[1]。由于价格风险对电力公司的利润影响最大，而市场价格具有很大的波动性，所以利用概率方法比较适合描述和规避电力公司面临的风险。

文献［2］采用了收益的均值和方差计量风险的Markowitz方差计量理论，具有较大的局限性，这种方法把收益的向上偏差和向下偏差都看成是风险，违背了购电决策者对于风险的真实感受，且其资产组合理论所依赖的一系列假设往往难以满足,如收益率假定为只服从标准的正态分布，而忽略了其他可能的分布，因而该方法在资产组合的风险分析中并不适用。文献［3］采用借鉴了风险价值（VaR）理论，来量化度量风险，但是其不满足可加性、次可加性和凸性，以及尾部损失测量不充分性[4]。鉴于VaR的上述缺陷，文献［5］采用其修正方法CVaR（Conditional Value-at-Risk）对供电公司的风险进行度量，从风险理论分析角度上看，这种方法比较合理。但是由于CVaR方法要求随机分布假定为单一分布的正态分布，实际上，由于电力市场收益率并不仅仅服从固定的分布。文献［6，7］提出，影响收益的因素还往往会服从多种分布，大多数情况下，市场的收益都会服从正态分布和对数正态分布，因此本文提出了加权条件风险价值（WCVaR）为风险指标的计量方法，引入可中断负荷这一种特殊的备用需求市场，建立电力公司在多能量市场的最优购电组合决策模型。

1 CVaR和WCVaR

1.1 CVaR的数学描述

CVaR也可称为平均超额损失（Mean Excess loss）、平均短缺（Mean Shortfall）或尾部VaR（Tail VaR），其含义可解释为：在一定的置信水平上（置信度），投资组合或工具的损失超过VaR的条件均值，反映了超额损失的平均水平。它比VaR更能体现投资组合的潜在风险。

设φ（u，y）表示损失函数，其中x∈X∪Rn为决策向量；y∈Rm为随机变量。随机变量y的概率密度为p（y），则 f（x，y）不超过给定限额 z的概率为

式中Ψ（x，z）为损失不超过α的累积分布函数，它随α是非减且右连续的。因此对于给定的置信区间α∈（0，1），及某一固定值 u为

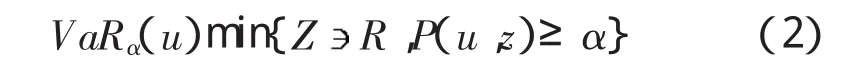
然而VaR存在较大的缺陷，如，不是一致性风险度量，不满足次可加性和凸性[8-9]，而且计算较为困难。鉴于此，Rockafeller和Uryasev提出了CVaR方法，它反应了风险超过了α-分位点的条件期望均值为

由于该式的计算比较困难，为此引入一个辅助函数来计算CVaR。

其中［x］+=max｛x，0｝，通常情况下，y的概率密度p（y）很难求出，因此可以采用蒙特卡洛法，采取样本点模拟样本数据y1，y2，y3，…，yq，则可近似为

1.2 加权条件风险价值模型WCVaR

利用CVaR来量化最优投资组合的风险，一般都要设定受市场的影响因素y的密度函数是单一的。在实际的投资中，影响收益率的因素往往不是仅服从单一的概率密度函数，而是受多种密度函数的共同影响，这时，就需要一种比CVaR更精确的方法来量化风险的指标，本文采取了加权条件风险价值WCVaR(Weighted Conditional Value-at-Risk)。假设受市场影响的因素yk的概率密度函数有n种，可用一个线性组合来表示总的分布函数，而每一种分布所占的比重为λT=[λ1，λ2，…，λn]，其中λ1+λ2+…+λn=1，则改进的WCVaR模型为

通过式（6），可对电力公司最优购电组合策略进行风险度量。

2 基于WCVaR的最优购电模型

随着电力市场的逐步开放和不断完善，负荷需求侧对电力市场的参与不断加大，电力市场具有更加明显的负荷不确定性和价格的波动性。因此，电力公司作为一个独立的经济体，需要优化在各种市场的投资组合策略，使得自身面临的风险最小，而总收益最大化。但是以往的研究都只是侧重考虑价格的波动，服从单一的正态分布情况下的最优购电侧率问题，本文则进一步考虑了用户端的参与，以及市场收益率为多种分布，如大多数情况下都是正态分布和对数正态分布的情况下，供电公司在多能量市场上的最优购电组合策略。

3 供电公司的多能量市场

本文将电力市场划分为合约市场、现货市场和可中断负荷市场。为便于数值的统一计算，本文将受益、电量分配风险指标都用百分比来表示。

3.1 合约市场

合约市场就是供电公司对未来一段时间内(一般在1个月或1周左右)的负荷做出预测，事先与用户签订合同，并规定了供电量和电价。

3.2 现货市场

现货市场是指供电公司在交易前的一段时间（通常是1天或是1 h前），根据负荷侧短期的预测为满足用户的实时需要在电力交易中心购入的电量，它的电量和价格的波动性要比合约市场的波动更大，因此它的风险更大，而相应的收益可能会更高。

3.3 可中断负荷市场

可中断负荷指在电网高峰负荷时段,或用户负荷中可以中断的部分。可中断负荷通常通过经济合同实现，是需求侧管理（DSM）的一部分[10]。可中断负荷在系统峰荷或故障时，可以减少负荷需求量,这等效于增加了备用容量，故可中断负荷通常被看做一种特殊的备用市场。

对于可中断负荷，如果系统照常供给能量，则用户需要以合同中的电能价格支付给供电方；如果备用容量不足，系统可以中断供给,这时供电方需要按合同赔偿用户。

4 基于WCVaR的多能量市场购电决策模型

本文主要研究的电力市场设定为包括合约市场、现货市场和可中断负荷的特殊备用市场。文献[11]考虑对可中断负荷的赔偿价格是固定的，而本文认为，这并不能真实地反映用户对于实际市场变化的真实感受，所以可中断负荷的电价应该由用户和电力公司事前商量好，随着实时价格的波动而波动，这样可以比较合理地补偿用户由于中断造成的损失。以往的大多数文件都只考虑负荷是固定不变的，或者说负荷预测是精确的，而本文引用了可中断负荷市场以后，无论负荷预测准确与否都可以衡量供电公司的购电风险。

4.1 研究条件

a）不考虑输电约束。

b）可中断负荷备用的价格高于中断发生时的实时市场价格。

c）考虑供电公司的实际情况。

d）长期合同市场、现货市场、可中断负荷备用市场的电价之间相互独立，不存在相关性。

4.2 数学模型

供电公司在合约市场中购入电量比率为x1，其电价为p1，其期望值和方差分别为μ1和δ21；在现货市场购入电量比率为x2，其电价为p2，其期望值和方差分别为μ2和δ22。剩下的电量在可中断备用市场中购买，可以理解为当系统发生故障时，需要切断的可中断负荷；或者是当出现在峰荷时，电力公司可以对可中断负荷用户拉闸限电，并对用户因负荷中断电量x3做出一个赔偿，价格为p3，该值是供电公司和用户事先制定的确定值。假设供电公司单位售电价为ps，为方便起见，写成向量的形式。

若负荷总需求固定为1，则有

则供电公司的购售电的收益函数为

收益的期望值为

方差为δ2（π）=xT∑x，该购电组合的成本表示其损失，即φ（x，p）=xTP 。

则，电力公司购电组合的CVaR函数为

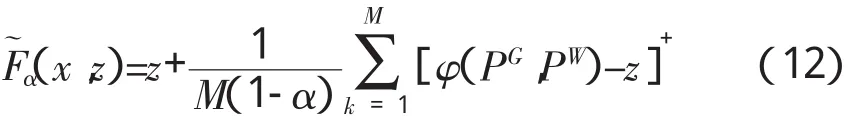
令γk=［f（x，yk）-α］+，γk≥0且γk≥f（x，yk）-α，k=1，2，…，q，于是式 （12） 可以简化为

供电公司的期望是收益最大化、风险最小化的双目标函数，即

为了计算的方便，把风险作为目标函数，收益作为约束函数，则收益为不小于给定的一个下限值；否则，不采取该购电决策。于是供电公司的购电决策就变成在收益不小于给定值下，求风险的最小。

在完全开放的电力市场环境下，电价的分布并不是单一的正态分布，经研究发现，很多时候特别是电力供应紧张时，电价的随机分布还趋向于对数正态分布。本文主要考虑了以上两种分布，设每一种分布所占的比重分别为λ1、λ2，写成λT=[λ1，λ2]，在每一种分布下，取相同的样本数，则WCVaR的函数为

以最小化风险为目标，在某种置信水平β下，供电公司购电组合的均值β-WCVaR购电模型为式（15），它是一个线性函数，故电力公司的购电决策优化模型可以转化成简单的线性随机优化问题。

式中，z为VaR的值，W为供电公司收益的下限。综上所述，模型（16）解析为：给定置信水平下，寻求最优的购电组合，使得收益满足给定值时，电力公司的WCVaR值达到最小。

5 研究问题的实际意义

a）在高峰时段或出现电力事故时,用户可以根据自己的情况自行决定是否减少负荷的需求量,通过合同的方式和电力公司签订可中断负荷协议来参与可中断负荷管理项目，来达到减少电费支出，并获得回扣，方便用户节约用电成本。

b）电力企业实行可中断负荷管理的目的是平稳负荷曲线，保证电力系统的安全稳定运行，缓解电力紧张时期，特别是季节性峰荷时的供电压力，以及电力事故时期提高电网的应变能力，方便电力公司安排检修计划等等，同时兼顾经济效益的提高，降低运行成本。

c）激励了用户积极参与到市场的互动当中来，有利于提高居民节约用电意识，缓解能源供应紧张的局面，有效降低碳的排放量，提高资源利用效率，达到节能环保以及可持续发展的目的。

［1］ 郑风雷，文福拴，吴复立.电力市场环境下的输电投资与扩展规划［J］.电力系统自动化，2006，30（10）:80-86.

［2］ Markowitz H.Portfolio Selection［J］.Journal of Finance，1952，3（7）：77-91.

［3］ 姚京，李仲飞.基于VaR的金融资产配置模型［J］.中国管理科学，2004，12（1）：8-14.

［4］ R.T.Rockafellar，S.Uryasev.Optimizationof conditional value-at-risk［J］.The Journal of Risk，2000，2（3）:21-41.

［5］ 王壬，尚金成，冯旸，等.基于CVaR风险计量指标的发电商投标组合策略及模型［J］.电力系统自动化，2005（14）:13-15.

［6］ 刘皓明，韩蜜蜜，侯云鹤，等.供电公司多能量市场最优购电组合的加权CVaR模型.［J］.电网技术，2010，34（9）:133-138.

［7］ 林辉，何建敏.VaR在投资组合应用中存在的缺陷与CVaR模型［J］.财贸经济，2003（12）:46-49.

［8］ Pavlo K，Jonas P，Uryasevs.Portfolio Optimization with Conditional Value-at-Risk Objective and Constraints［J］.The Journal of Risk，2002，4（2）:11-27.

［9］ R.T.Rockafellar.Coherent Approaches to Risk in Optimization［J］.Tutorialsin Operations Research Informas，2007（4）:38-61.

［10］ 王瑞庆，李渝曾.计及可中断负荷对现货电价影响的供电商负荷消减策略［J］.电网技术，2004，28（18）:16-20.

［11］ 方勇，李渝曾，张少华.电力市场中电力公司应用可中断负荷管理的方法［J］.电力系统自动化，2004，28（18）:16-20.