基于实数编码量子进化算法的IIR数字滤波器优化设计
哈尔滨电气集团阿城继电器有限责任公司 孙成发
1.引言
IIR数字滤波器是一类重要的滤波器,具有较高的计算精度,且能够用较低的阶数获得很好的频率选择特性,已在很多领域得到了应用。IIR数字滤波器设计是信号处理中的一个重要课题。许多学者在IIR数字滤波器设计方面作了大量的工作[1-4],主要分为两类:一类是先设计模拟滤波器,然后利用双线性变换转变为数字滤波器,方法简单易行,但设计结果有时不是十分理想[1];另一类是基于某一优化准则,将数字滤波器设计问题转化为优化问题的求解,以使设计的数字滤波器性能达到最优,但由于相应的优化问题均是复杂的多参数非线性函数优化问题,在求解过程中极易陷入局部极值,难以得到全局最优解或满意解。近年来,随着智能优化算法的发展,已有学者将遗传算法(GA)[2]和粒子群算法(PSO)[3,4]应用到IIR是字滤波器设计中,但GA算法存在着难以克服的“早熟”和“停滞”问题;PSO虽然运行速度快,简单,但仍有很大可能陷入局部极值。
实数编码量子进化算法(Read-coded quantum evolutionary algorithms,RQEA)是基于量子计算的相关概念和原理形成的一种概率性搜索算法,具有收敛速度快,全局搜索能力强的特点[5,6]。RQEA为数字滤波器的设计提供了一种新的工具,文中将RQEA用于IIR数字滤波器的优化设计,给出了IIR数字滤波器设计的优化模型,介绍了RQEA的基本原理和应用RQEA设计IIR数字滤波器的具体实现过程,最后,通过仿真试验表明应用RQEA设计IIR数字滤波器不仅可行,而且有效。
2.IIR数字滤波器优化设计
2.1 IIR滤波器的优化模型
设N阶IIR数字滤波器的传递函数描述为:

如采用(1)式进行IIR数字滤波器设计,则待优化参数共有M +N+2个,且各参数的取值范围难以确定。为了便于采用优化算法进行IIR数字滤波器优化设计,通常采用二阶节的级联结构形式对(1)式进行变形,即:

式中A是增益,是一个常数,N为二阶节的个数,ak、bk、ck和dk是待优化设计参数。当IIR滤波器采用(2)式结构时,频率响应对系数变化的敏感度低,便于调整频率响应。(2)式对应的IIR数字滤波器的频率响应为:

式中:


2.2 参数取值范围的确定
将(3)式代入(5)式得:

可见,E是增益A和滤波器系数ak、bk、ck和dk(N k=1,…,)的非线性函数,而增益A不是独立参数,可由其它参数参数确定,则优化问题(5)式含有4k个参数。
将(6)式对A求微分并令其为0,可推导出最佳增益A的解析表达式,即:
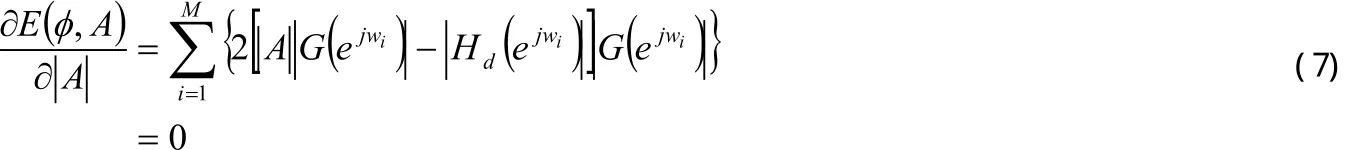
可得:


表1 IIR数字滤波器设计结果Table1 Results of IIR digital filter design

图1 不同算法进化过程Fig.1 Evolutionary procures of different algorithms
由于只考虑幅度响应误差,A的正负值对结果没有影响。但是,为了保证设计滤波器的稳定性,需要对优化参数范围进行限制。由(2)式可知,只要使每个二阶节的极点都在Z平面的单位园内,即:的零点zk都满足由此可以确定ck和dk的取值范围为:-2<ck<2,-1<dk<1,(k=1,…,N )。若参数在此范围内取值,优化结果仍然出现不稳定极点,可以用该极点在单位圆内的映像代替该极点(相当于级联了一个全通网络),可以在不改变滤波器幅频响应的基础上,保证得到稳定的滤波器。如果要求设计的滤波器同时具有最小相移特性,对ak和bk的取值范围作同样的限制。
3.实数编码量子进化算法(RQEA)
RQEA基本思想[5]:(1)构造实数编码三倍体染色体;(2)利用量子旋转门和基于高斯变异的互补双变异算子一起进化染色体;(3)通过离散交叉实现染色体之间的信息交流,扩大算法搜索范围;(4)采用“爬山”选择,加快算法收敛速度。
实数编码三倍体染色体的等位基因由复杂函数自变量向量x的一个分量xi和量子比特的一对概率幅组成,即:,则实数编码三倍体染色体可描述为:

式中,αi和βi满足归一化条件,i=1,…,n。n为染色体长度,由复杂函数的维数决定。
RQEA对每一个染色体实施单基因变异[7]。设第t代时群体为N为群体规模。对于,随机选择第i基因位对变量进行高斯变异,可得:
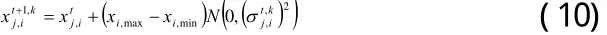
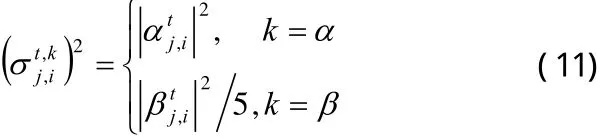

图2 不同算法设计滤波器幅频特性Fig.2 Magnitude of filter designed by different algorithms
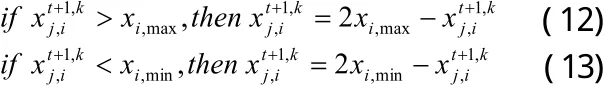
若由(10)式生成的新染色体优于原染色体,则为有效进化,可令否则为无效进化,并由量子旋转门更新和,即:
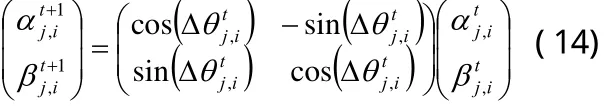

式中,θ0为初始旋转角,γ为进化尺度,θ0和γ控制旋转角大小;符号函数sgn(·)控制旋转角方向,以确保算法收敛。
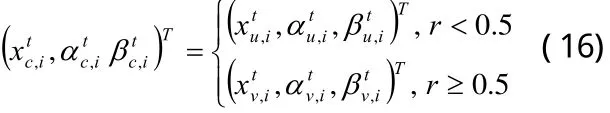
4.算例分析
为了验证文中提出方法的有效性和优越性,采用RQEA设计低通滤波器(例1)和高通滤波器(例2),同时,出于比较的目的,采用GA求解相同的问题。
例1:设计一个低通滤波器,其技术指标为:
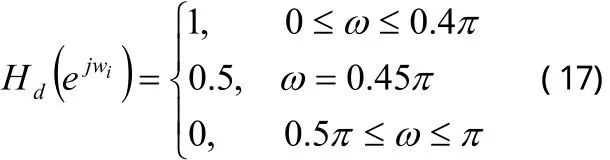
例2:设计一个高通滤波器,其技术指标为:
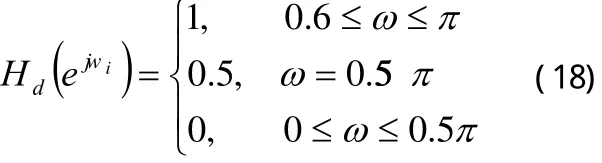
在例1和例2中,数字滤波器均选用3个二阶节,即N=3,则滤波器参数共有个,频域采样点数均取为21。RQEA相关参数为:群体规模、初始旋转角θ0=0.3π、进化尺度、实数编码三倍体染色体基因位中的概率幅均取为连续“求精”和“求泛”次数分别为mf=6,mc=2;GA相关参数为:群体规模,是RQEA群体规模的2倍,最优个体保留,蒙特卡罗选择,交叉概率pc=0.7,变异概率pm=0.1。两种算法均以运算代数作为终止条件,且运算代数取为500,为消除单次运算存在的偶然性,各种算法均在给定参数下独立运算10次,取其中最好的一次作为最终优化结果。图1描述了设计数字滤波器的优化过程。图2描述了设计数字滤波器的幅频特性。
由图1可以看出,RQEA无论是收敛速度,还是优化结果均优于GA。由图2不难发现,应用RQEA设计的数字滤波器的通带波动、过度带斜率以及阻带衰减均要优于GA设计的数字滤波器,应用RQEA设计数字滤波器具有更好的综合性能。表1列出了数字滤波器设计结果,滤波器各个参数均保留6位小数,能够发现RQEA设计数字滤波器与理想滤波器的均方误差更小,性能更优。
5.结论
鉴于IIR数字滤波器优化设计本质上是一个多维非线性函数优化问题,文中将具有全局收敛性好,收敛速度快特点的RQEA引入IIR数字滤波器设计中。仿真实验表明,应用RQEA优化设计IIR数字滤波器较GA具有更优良的性能,具有实际意义。
[1]Deckey A G.Synthesis of Recursive Digital Filters Using the minimum P-error Criterion[J].IEEE Trans.Audio Electroacoust,1972,20:257-263.
[2]李建华,殷福亮.设计IIR数字滤波器的遗传优化算法[J].通信学报,1999,17(3):1-7.
[3]侯志荣,吕振肃.IIR数字滤波器设计的例子群优化算法[J].电路与系统学报,2003,8(4):16-19.
[4]张松华,陆秀令.IIR数字滤波器的粒子群优化设计方法[J].信息与电子工程,2007,5(4):271-274.
[5]高辉,徐光辉,张锐,等.实数编码量子进化算法[J].控制与决策,2008,23(1):87-90.
[6]Gao H,Zhang R.Real-coded quantum evolutionary algorithm for global namerical optimization with continuous variables.Chinese Journal of Electronics(CJE),2011,20(3):499-503.
[7]王湘中,喻寿益.适用于高维优化问题的改进进化策略[J].控制理论与应用,2006,23(1):148-151.

