模糊自适应调整趋近律的导弹姿态滑模控制系统设计*
唐意东,李小兵,乔朋朋
(空军工程大学防空反导学院,西安 710051)
0 引言
利用变结构控制响应快速、对参数变化和扰动不灵敏的特点,可以实现对系统较好的控制。但是,在控制过程中,系统状态及控制量的变化不可能瞬间发生,即不可能产生连续的变化。由于惯性引起滞后的原因,切换函数在不断切换的过程中必然会产生抖动。对于如何削弱滑模变结构控制中的抖振,文献[1]采用连续化法,用饱和型切换代替继电型切换,即所谓的“边界层”法。但是在引入饱和型切换后,系统已经不是变结构系统,自然也就失去了变结构控制系统最大的优势——对参数摄动和扰动的鲁棒性。而且对于非线性系统,即使在边界层内同样存在抖动[4]。文献[2]则用饱和非线性函数代替符号函数,式中δ的选择对去抖有较大影响。这种滑模变结构控制方法,是通过确定δ的值,在牺牲了一定动态品质的前提下,较好的实现对系统抖振的削弱。文献[3]设计一种最终滑动模态变结构控制系统,在受到扰动的时候需要6s的过渡时间,这对于工作时长在60s左右的某型地空导弹来说显然是不可接受的。对地空导弹这一类需要在不确定环境下工作,对快速性和鲁棒性都有着较高要求的系统来说,寻找一种可以兼顾两方面性能的控制方法是有实际意义的。
针对上述情况,文中引入李士勇提出的将模糊控制与常规滑模变结构控制结合的控制方法,给出了一种基于模糊自适应调节的滑模变结构控制律,保证了系统的快速收敛性和对外部扰动的鲁棒性。利用模糊控制的柔滑控制信号,有效的削弱了滑模变结构控制过程中产生的抖振。最后,将这种方法应用于某型防空导弹的姿态控制系统,验证了该方法的有效性。
1 导弹姿态控制模型建立
弹体环节的运动微分方程一般讲应为非线性、变系数、三维联立微分方程组。但是,地空导弹在许多场合是在铅垂平面或者倾斜平面内飞行。因此,可以考虑短周期内导弹特征点工作状态[6],利用小扰动假定、结构参数连续变化假定和固化系数法,得到有侧滑无倾斜水平面导弹运动微分方程:
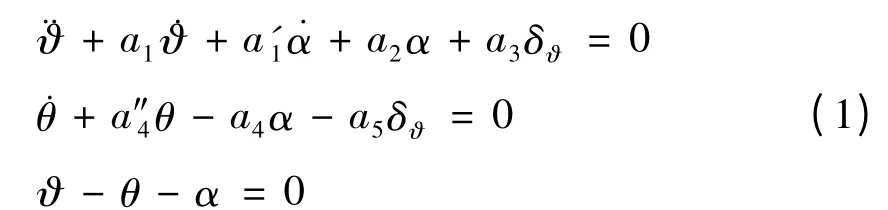
方程(1)中a'1表示气流下洗延迟对弹体转动的影响,其值远比a1、a2小,故可以忽略。同时忽略重力系数a″4的影响,根据理想操纵关系ε=0得ϑ =α。则可以得到导弹运动状态方程:
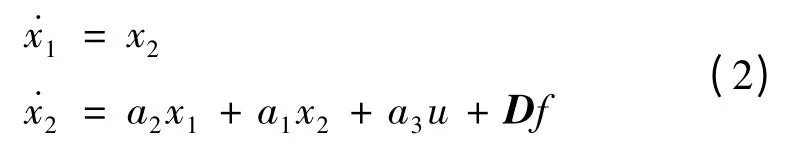
式中:u为俯仰舵偏角δϑ,f为外部干扰,‖f‖ <F为有界干扰。
2 控制器设计
2.1 滑模变结构控制器设计
由方程(2)可得系统状态方程为:

切换函数s=Cx,C= [c,1]。运用任置滑动模态特征向量的方法来确定C阵。由等效控制:

可得u=(CB)-1CAx,则滑动模态方程为:
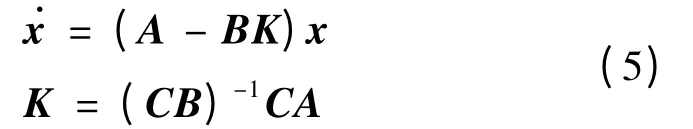
滑动模态发生于Ker(C)=N(C)之内。给定λi(i=1,2,...,n)为滑动模态的特征根。由
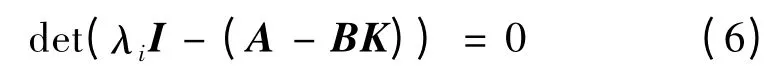
可解得c,即得C阵。
选取指数趋近律:

式中ε的取值决定了到达滑动模态的速率和抖振程度。由式(7)可得控制为:

2.2 模糊控制器设计
定义模糊子集{NB,NM,NS,ZO,PS,PM,PB},根据模糊控制原理,定义s和˙s为模糊控制器的输入,fs为模糊控制器的输出,其论域为:
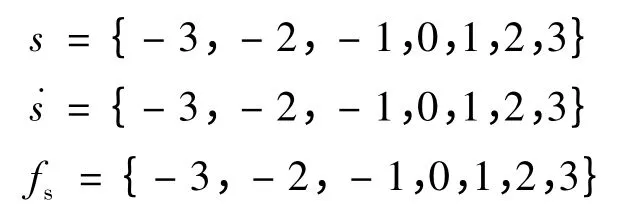
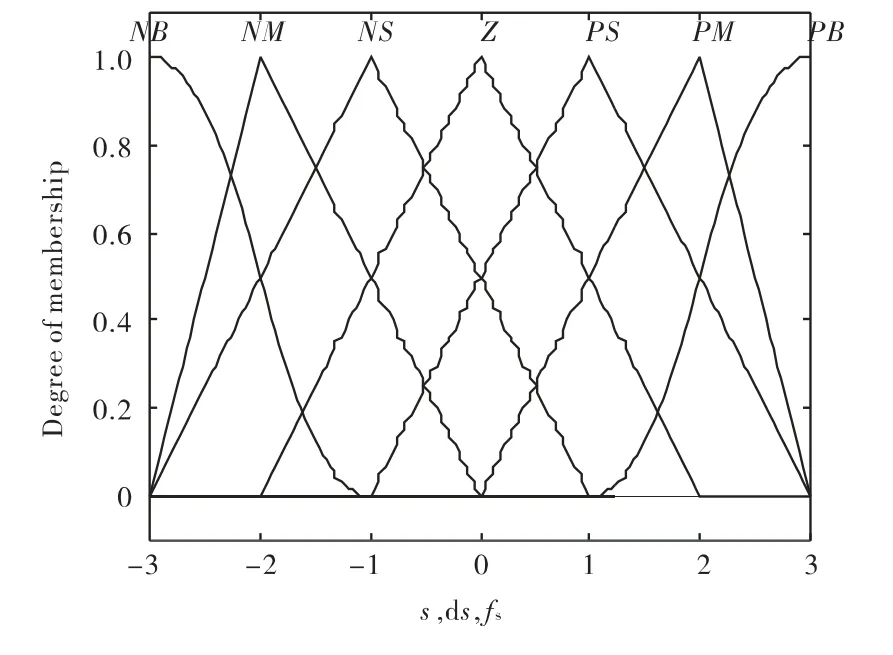
图1 s,和fs的隶属函数
模糊控制规则如下:
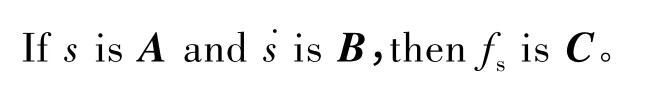
在力图满足不等式s˙s<0的条件下设计控制律使得滑动模态有较快的到达速率,又要在接近滑模面时减小速率,削弱干扰。所获得的控制规则见表1。

表1 模糊控制规则表
用Ri1·Ri2表示一条语句所确定的模糊关系,可以算出模糊控制量

同理可以根据其余各条语句得到模糊控制量ˉfs,,控制量的模糊集合可以表示为:
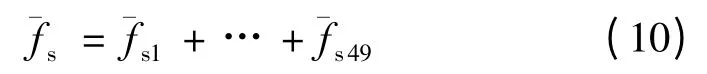
非模糊化过程采用MIN-MAX-重心法,其实质是加权平均法。调整加权系数可以改善系统的响应特性,即调整各论域内元素对模糊语言变量的隶属度。
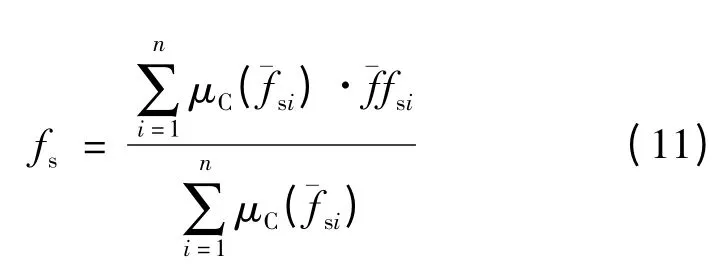
2.3 抗摄动及干扰能力分析
系统(3)受干扰和参数摄动情况。令˙s=C˙x=C(A+ΔA)x+CBu+CDf=0,设CB为非奇异阵,解出等效控制:

代入方程(3)得到描述滑动模态的运动微分方程:
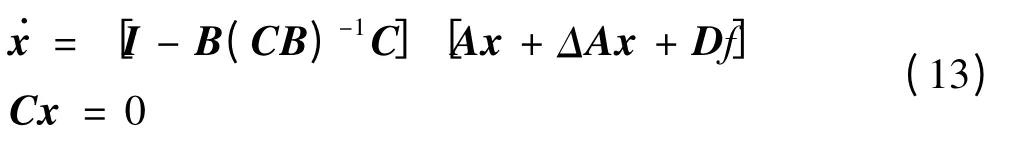
当[I-B(CB)-1C]Df=0时,干扰f将不会对滑动模态发生作用。因此滑动模态不受干扰f影响的充分必要条件为[4]:

当[I-B(CB)-1C]ΔAx=0时,参数摄动ΔA将不会影响到滑动模态。因此不变性成立的充分条件为:

3 仿真及结果分析
根据设计的控制律,以某型地空导弹俯仰通道姿态控制系统为例进行仿真研究,取参数q=97568,s=0.2552,l=0.57,v=400,Jy=3996,g=9.81,=-0.18=-0.28,=-128,输入信号为正弦叠加信号,有界干扰f≤0.01。

图2 滑动模态变化曲线
图2 为滑动模态在到达切换面过程中的变化曲线,可以看到,模糊自适应调剂的滑模变结构控制过程中,滑动模态能够更快的到达切换面,并且能够有效的削弱抖振。图3和图4分别为模糊自适应调节滑模变结构控制量和常规滑模变结构控制量的变化曲线,由于输入是正弦叠加信号,因此控制量周期性变化。同样,模糊自适应滑模变结构控制能够有效削弱控制量的抖振。图5和图6分别为误差e和误差变化率˙e相轨迹图和局部放大图,可以看到,模糊自适应滑模变结构控制的相轨迹以较小的角度平滑的接近切换面。图7和图8分别为对正弦叠加信号的跟踪误差及其局部放大图,可以看到误差在t=0.35s是收敛为零,说明系统稳定,收敛时间可控且有限。仿真结果表明,基于模糊自适应调节的滑模变
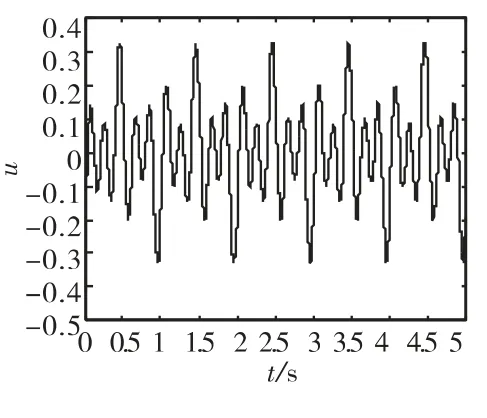
图3 自适应调节滑模变结构控制量变化曲线
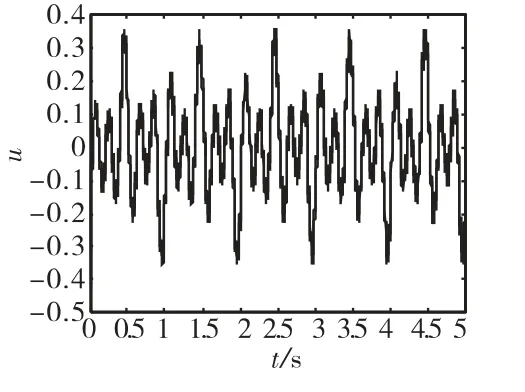
图4 常规滑模变结构控制量变化
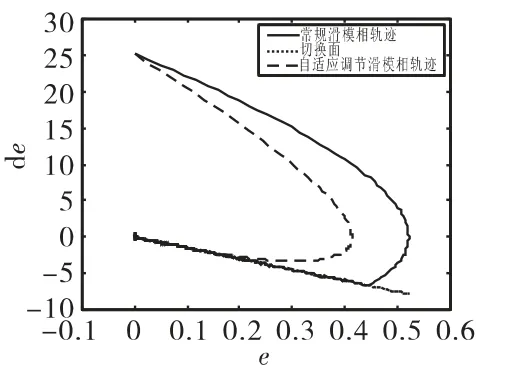
图5 相轨迹

图6 相轨迹局部放大图

图7 俯仰角ϑ位置跟踪

图8 俯仰角ϑ位置跟踪局部放大图
结构控制能够使导弹稳定可靠的对输入信号实现跟踪,并且能够在保持常规滑模变结构控制鲁棒性的同时,有效削弱滑模变结构控制产生的抖振。
4 结论
通过分析传统滑模控制的特点,考虑系统外部有界干扰和参数摄动,将模糊控制的相关理论与传统滑模变结构控制相结合,设计了一种基于模糊自适应调节的滑模控制方法。能够保证系统的快速性和鲁棒性,优于常规滑模变结构控制。文中对系统进行了小扰动假设和固定系数处理,对于充分考虑时变和不确定系统的情况可以引入一类自适应辨识方法对参数进行在线辨识[8]。
[1]赵宏战,周军.防空导弹姿态控制系统终态滑模变结构设计[J].计算机仿真,2009,26(2):73 -76.
[2]胡龙兵,李言俊.一种改进的变结构制导律的设计与仿真[J].火力与指挥控制,2010,35(9):193 -194.
[3]戚京锋,周凤岐.最终滑动模态变结构导弹控制系统设计[J].弹箭与制导学报,2004,24(3):273 -275.
[4]高为炳.变结构控制理论基础[M].北京:中国科学技术出版社,1990.
[5]张翼飞,杨辉,邓方林.二阶系统模糊变结构控制器设计及稳定性分析[J].系统工程与电子技术,2005,27(2):312-315.
[6]陈佳实.导弹制导和控制系统的分析与设计[M].北京:宇航出版社,1989.
[7]刘金琨.滑模变结构控制MATLAB仿真[M].2版.北京:清华大学出版社,2012.
[8]韩曾晋.自适应控制[M].北京:清华大学出版社,1995.

