单轴旋转引起加速度计尺寸效应误差分析及补偿*

梁茂柱，王 超，杜鹏程

(1 91040部队，山东青岛 266100;2海军潜艇学院，山东青岛 266044;3 92196部队，山东青岛 266000)

0 引言

单轴旋转惯导系统通过旋转机构周期性旋转能够补偿惯性元件常值漂移在转轴垂直方向上分量以及部分安装误差[1]，在系统中引入阻尼，可以消除系统的舒拉周期和傅科周期振荡误差，同时抑制随机漂移的影响，提高系统的精度。

在系统转台旋转时，会产生加速度计尺寸误差效应[2]，相当于加速度计的常值漂移，虽然在长时间导航过程中，通过旋转能够使由尺寸效应误差产生的导航位置误差相互抵消，不会累积[3]，但加速度计尺寸效应误差会增加系统速度误差的振荡幅值，降低系统的速度精度;此外，对水平阻尼单轴旋转惯导而言，由加速度计尺寸效应产生的加速度相当于载体的伪加速信号，这个信号将对不满足舒拉调谐条件的阻尼系统产生较大的动态误差。文中重点对由单轴旋转运动引起的加速度计尺寸效应误差及其影响进行分析，并给出了补偿方法。

1 单轴旋转引起的加速度计尺寸效应误差分析

惯导系统通常采用3个一组的加速计测量沿3个正交轴方向的运动，得到作用在载体上的比力。在理想情况下，3个加速度计需要准确安装在载体的同一位置，显然，这是不可能实现的，因为加速度计有一定的尺寸，并且惯导系统的硬件安装位置也受到限制，由于加速度计相对于理想位置存在物理偏差，其敏感到的切向力和向心力被称作加速度计的尺寸效应[2]。

只要安装在载体上的惯导系统的加速度计组件姿态相对惯性坐标系发生变化，由于尺寸效应，加速度计就会产生测量误差，这种误差与加速度计的缺陷无关，即使惯性导航系统采用没有任何误差的加速度计，仍然存在尺寸效应误差。文中不考虑由于载体机动以及海浪等因素导致载体姿态发生变化而产生的尺寸效应误差，考虑地球自转，分析单轴旋转引起的加速度计的尺寸效应误差。

如图1所示，OENU为当地地理坐标系(导航坐标系)，Oxryrzr为旋转坐标系，初始时刻，旋转坐标系Oxryrzr与OENU重合，坐标系Oxryrzr绕OU轴以角频率ωr单向旋转，3个加速度计分别放在旋转坐标系Oxryrzr的坐标轴上，距离理想点O的距离为l。地球自转角频率为ωie，当地地理纬度为φ，t时刻Oxryrzr坐标系转过ωrt角度，令绕Oxr轴、Oyr轴和Ozr轴的角频率分别ωxr，ωyr和 ωzr，则:

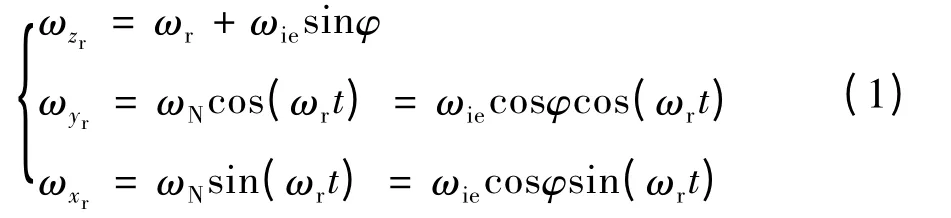
图1 速度计组件坐标系相对导航坐标系变化示意图

则Oxr、Oyr轴上px、py点受到的绝对加速度分别为:

式中:fx1、fy1分别为 px、py点的离心加速度，fx2、fy2分别为px、py点的切向加速度，其中:

由于ωr和ωie为定值，所以fx2=fy2=0，可以忽略加速度计的测量值中的切向力，将式(1)代入式(2)，由于 ωie≪ ωr，化简得 Oxr、Oyr轴加速计测得比力的大小分别为:

将加速度计尺寸效应误差转换到导航坐标系下，得到载体等效东向和北向伪加速度分别为:

由式(8)和式(9)可知，在旋转过程中，加速计尺寸效应误差将引起载体的伪加速度，这个伪加速度呈现周期性振荡形式，载体东向和北向伪加速度的最大值为，该伪加速度将增加系统速度的振荡幅值，影响惯导系统输出的速度和姿态精度;在一个旋转周期内，分别对式(8)和式(9)进行积分，积分值为零，可见，在长时间的导航过程中，单轴旋转使由加速度计尺寸效应误差引起的误差相互抵消，不会引起误差的发散。

以系统导航计算平台北向通道为例，说明等效北向加速度误差对系统速度误差影响，如图2所示。

在无阻尼条件下，北向加速度误差δfN(s)到系统速度误差δVN(s)的传递函数为:

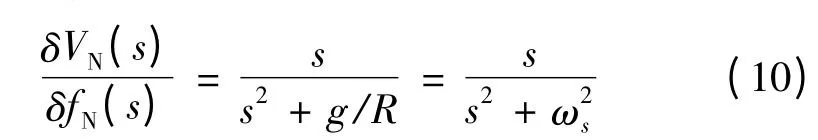
图2 无阻尼单轴旋转惯导北向通道方块图

由式(8)得:

将式(11)代入式(10)得:

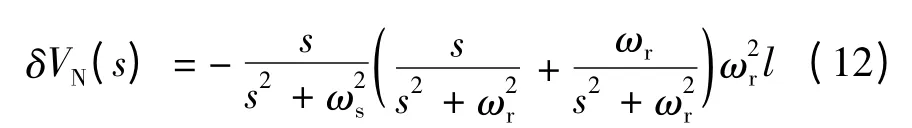
对式(12)两边取拉普拉斯反变换，得到北向速度误差的时域表达式:

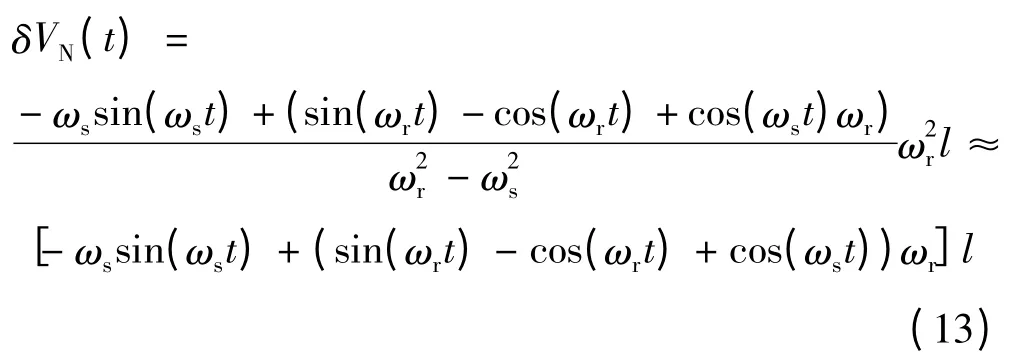
由式(7)和式(13)可知，由旋转引起的加速度计尺寸效应误差可以等效为加速度计的常值漂移，与和l成正比;由加速度计尺寸效应误差引起的速度误差与ωr和l有关，速度误差的极值随着ωr的增大而增大。当 ωr=18°/s，l=0.1m 时，引起的加速度计常值漂移约为0.0098696m/s2，引起的速度误差的极值约为 0.14kn。

在水平阻尼条件下，由旋转运动引起的速度误差的频域表达式为:H(s)为加入的校正网络[4]。在系统中加入校正网络，系统变成阻尼系统，将不满足舒拉调谐条件，在等效北向伪加速度的作用下将产生动态误差。由于在水平阻尼条件，求解北向速度误差δVN(t)的时域表达式较为复杂，不便分析，后面将通过计算机仿真的方法，分析加速度计尺寸效应误差引起的速度误差。

2 加速度计尺寸效应误差的补偿

通过以上分析可知，加速度计尺寸效应误差跟旋转机构的转速有关，为降低尺寸效应引起的误差，可以在进行旋转方案设计时采用较低的旋转速度降低尺寸效应误差，但这会影响对其它误差的补偿效果[5]。由式(7)可知，在旋转过程中，根据旋转机构的转速可估计产生的加速度计尺寸效应误差，把估计的误差补偿到加速度计的测量值中，再将补偿后的加速度信息送入导航计算机进行导航解算，即可实现对加速度计尺寸效应误差的补偿，此方法简单易于实现，其补偿原理如下式所示:

其中:ax、ay分别为两个水平加速度计测得的比力，fxr、fyr为由于旋转引起的加速度计尺寸效应误差、为补偿后的比力。经过补偿后，将大大降低加速度计测量值中的尺寸效应误差，减小由尺寸效应误差引起的系统水平速度误差和姿态角误差。

3 仿真分析

采用单轴正反转停方案[6]，旋转周期为20min，旋转时间为2min，停 止 时间为 18min，加速度计敏感中心到理想位置点的距离为0.1m，纬度为36°，只考虑单轴旋转惯导系统中的加速度计尺寸效应误差。采用时间步距仿真技术，分析加速度计尺寸效应误差对系统精度的影响，并验证对加速度计尺寸效应误差补偿的效果。仿真结果分别如图3和图4所示。A表示在水平阻尼工作状态下，没有补偿加速度计尺寸效应误差系统输出的位置误差曲线;B表示在无阻尼工作状态下，没有补偿加速度计尺寸效应误差系统输出的位置误差曲线;C表示在水平阻尼工作状态下，补偿加速度计尺寸效应误差后系统输出的位置误差曲线。

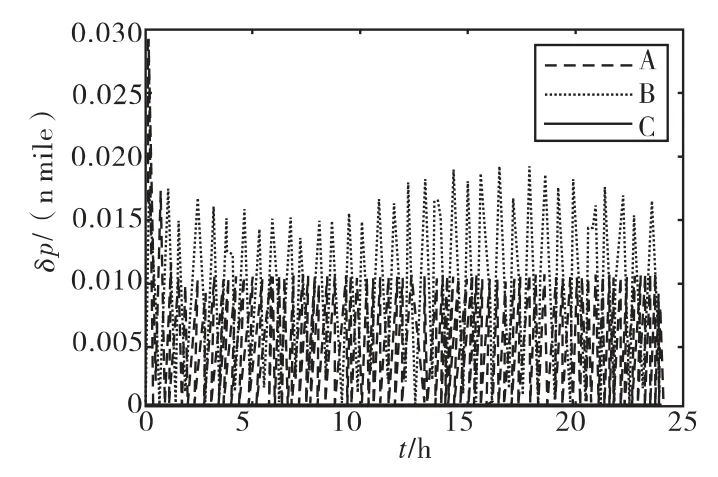
图3 位置误差曲线

从图3中可以看出，在无阻尼条件下，加速度计尺寸效应误差将引起系统位置误差的振荡，但不会引起系统位置误差的发散，最大位置误差约为0.02n mile;在水平阻尼条件下，位置误差发生以旋转周期为周期的振荡，最大误差约为0.012n mile，对加速度计尺寸效应误差进行补偿后，系统的位置误差非常小，可以忽略不计。

从图4中可以看出，在无阻尼条件下，加速度计尺寸效应误差将引起系统速度误差的振荡，振荡误差的最大值约为0.14kn，与前面理论分析一致;在水平阻尼条件下，系统受到伪加速信号的影响，将产生动态误差，最大误差约为0.15kn，补偿加速度计尺寸效应误差后，系统输出速度误差约为0，可以忽略不计。

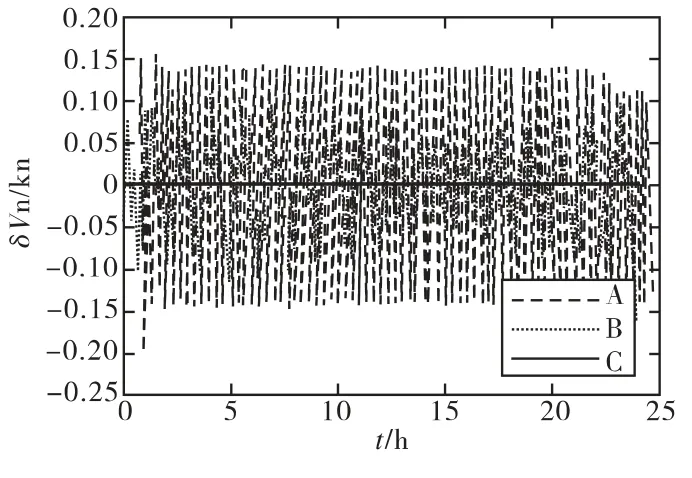
图4 北向速度误差曲线

4 结论

单轴旋转惯导系统在旋转过程中，会增大加速度计的尺寸效应误差，相当于加速度计的常值漂移，将误差变换到导航坐标下，相当于测得的载体伪加速信号。在长时间导航过程中，由于旋转可以实现误差的相互抵消，不会引起系统导航定位误差的发散。然而，在系统旋转过程中，这个加速度将增加无阻尼系统姿态角误差和水平速度误差的振荡幅值;对水平阻尼单轴旋转惯导而言，由于不满足舒拉调谐条件，受到伪加速信号的影响，将产生较大的动态误差，严重影响系统输出的水平速度和姿态角精度。通过补偿由旋转导致的加速度计尺寸效应误差，可有效降低系统的振荡误差，提高系统在旋转过程中输出的速度、姿态精度。

[1]袁保伦，饶谷音.光学陀螺旋转惯导系统原理探讨[J].国防科技大学学报，2007，28(6):76－80.

[2]David H Titterton，John L Weston.捷联惯性导航技术[M].张天光，王秀萍，王丽娜，等，译.北京:国防工业出版社，2007.

[3]袁保伦.四频激光陀螺旋转式惯导系统研究[D].长沙:国防科技大学，2007.

[4]陈永冰，钟斌.惯性导航原理[M].北京:国防工业出版社，2007.

[5]于旭东，王宇，张鹏飞，等.单轴旋转对惯导系统误差特性的影响[J].中国惯性技术学报，2008，16(6):643－648.

[6]海娜，陆全聪，黄昆，等.旋转式光学陀螺捷联惯导系统的旋转方案设计[J].中国惯性技术学报，2009，17(1):8－14.