Vague集理论在组合导航算法评价中的应用*

周 江，王仕成，赵 欣，张合新，张金生

(第二炮兵工程大学，西安 710025)

0 引言

随着组合导航信息融合算法种类的增多，各算法的品质研究和应用选取成为一个迫切需要解决的问题。然而，目前在这方面的研究成果还比较少。许多学者对系统、工程、质量等的评价进行了较为深入的研究，其中一些可以在本研究领域中对比借鉴，但它们却有自身的局限性。文献[1]采用简单的加权模型对组合导航算法进行评估，而权值的选取规则不明确，说服力不强;文献[2－3]采用三角模糊数的方法对系统进行评价，但它要先通过专家打分来建立判断矩阵，然后再求解，主观性太强;文献[4]采用模糊模式识别的方法，但它采用专家设定评价指标的满足范围，可执行性不强，以上三种方法都局限于人为假定某些条件，结果的正确性有待进一步研究。

Gau和 Buehrer[5]于 1993 年提出了 Vague集理论，这一理论的进一步研究成果可以用于解决多指标体系的综合评估问题[6－7]。文中即是针对实验测得的数据采用基于改进的Vague集多目标决策的模糊值线性序法来评价组合导航信息融合算法的优劣。采用属性测度理论求取Vague值和组合权重法求取权重值，使评价方法更为客观。首先确定算法的评价指标体系，然后分析Vague集理论在组合导航数据融合算法上的运用，最后实例分析验证其可行性。

1 评价指标体系的建立

分析一个控制系统的性能，可以从稳定性、准确性和快速性三方面考虑。对于数据融合算法评估来说即鲁棒性、滤波精度和实时性。而对算法评估不得不考虑导航量出现野值或者故障时算法的处理能力，即算法的可靠性。当出现少量野值时，希望算法仍能够正常工作且保持一定的精度，即算法的容错性，当出现故障时，希望算法能够诊断出故障并将其有效地去除，即算法的诊断率。

由此，确定出组合导航的信息融合算法品质评估指标为:滤波精度、实时性、鲁棒性、容错性以及诊断率5个指标，具体表示如图1所示。

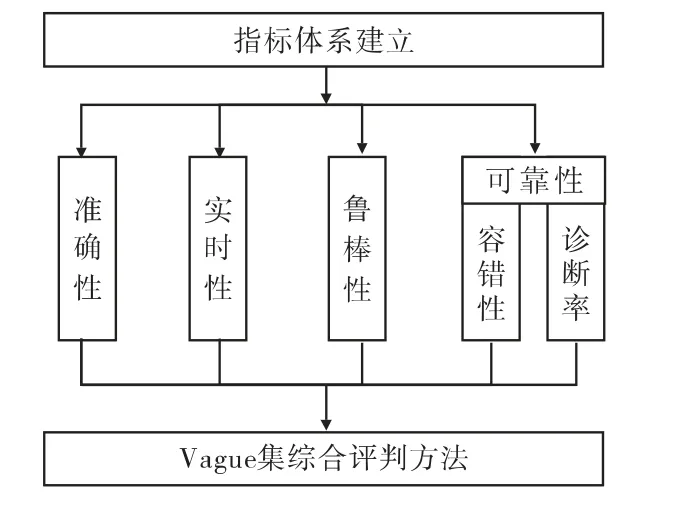
图1 算法指标体系及评估方法研究框图

文中采用文献[1]中对各个指标建立的计算标准为基础，从而由实验测得的数据计算出精度、鲁棒性、容错性和实时性4个指标的取值。

精度:

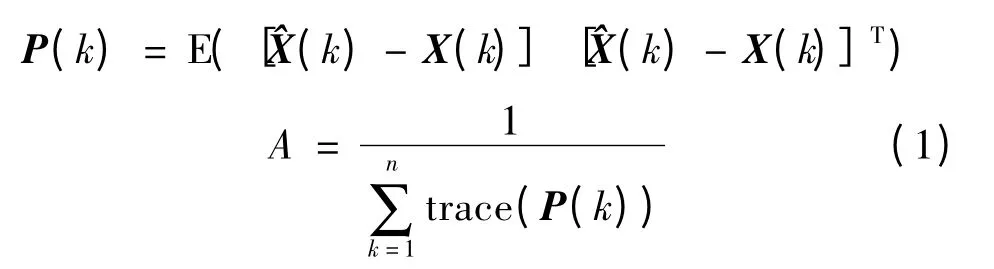
鲁棒性:

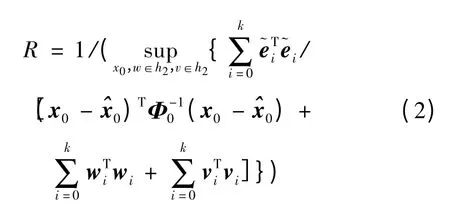
容错性:

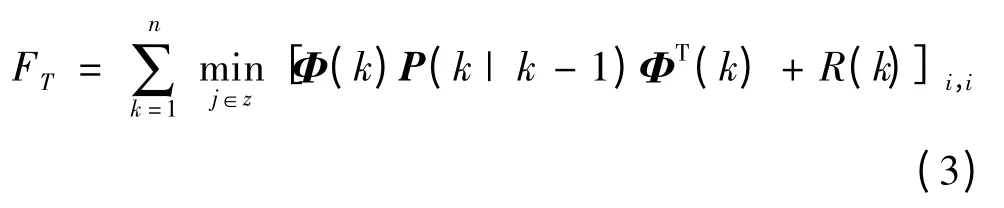
其中P(k|k－1)为预测误差协方差阵。

实时性:

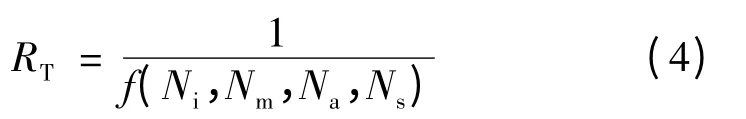
其中:Ni表示滤波器所需的矩阵求逆个数，Nm、Na分别表示滤波器一个滤波周期所需的乘法、加法个数，Ns表示滤波状态数。

诊断率描述的是算法去除故障识别正确的能力，由此可以定义:诊断率为算法在识别样本数据时，正确识别的样本数占输入样本总数的比例。即:

诊断率:

2 改进的Vague集多指标决策模糊值线性序法

2.1 Vague集理论基本原理及方法

Vague集理论是解决多目标决策的一种非常有效的方法[8]。例如在一次投票选举模型中有10人参与，候选者A有5人投支持票，2人投反对票，3人投弃权票;候选者B有4人投支持票，0人投反对票，6人投弃权票。面临这种抉择时，该选举谁呢?对信息融合算法评价也是如此，用N组指标来评价M种算法，其中有一种算法所有指标都适中，而另外一种算法有些指标性能非常好，但它同时含有部分指标的性能很差。面临这种问题时往往就不好做出较客观的判断。然而，Vague集理论恰恰能够很好的解决这类问题。

Vague集理论的思想认为每个元素的隶属度可以分为支持、对立和中立的3个方面。设论域U={u1，u2，…，un}，其中元素 ui是所讨论的对象，U 上的一个Vague集是由一个真隶属度函数tij表示支持ui的下界和一个假隶属度函数fij表示反对ui的下界[9]，且tij+fij≤1。πij=1－tij－fij表示目标的犹豫度函数，由此就可确定 Vague值，记作 Vij= [tij，1 － fij]。

Vague集理论目前多采用评分函数法、相似度度量法等对问题进行决策。这些方法得到一定应用，但同时存在一些不足:

1)Vague值选取的不明确性。多数模型Vague值求取不像选举模型那样明确，这样就不得不依靠专家打分系统给值或者经验赋值。因此就增加了Vague值选取的片面性和复杂程度。

2)对某些决策问题无法做出判断。例如评分函数法[10]采用S=tij－ fij来评分，对tij=fij的情况却无法做出判断。

文献[11]提出了Vague集多目标决策的模糊值线性序法，通过模糊值转化，很好的解决了上述第二点不足，但它的应用又出现了新的问题:

1)模糊值转化分析不够全面，建立的转化公式说服力不强;

2)模糊值线性序排序规则考虑不够全面;3)用专家赋值法选取权重过于主观随意。针对上述问题，文中提出了改进的Vague集多目标决策的线性序法，具体思路和步骤见下文。

设有m种组合导航信息融合算法需要评价，即:A={A1，A2，…，Am}，针对文中评价指标有 5 个分别设为:C1、C2、C3、C4、C5，各个指标的权重取为 ω1、ω2、ω3、ω4、ω5，且 ω1+ ω2+ ω3+ ω4+ ω5=1。

2.2 Vague值的确定

针对组合导航数据融合算法进行多目标决策时，并没有确定的Vague值数据，只有定量的指标，所以要解决将定量数据与Vague值数据相结合的问题。文中的解决方案:利用属性测度理论[12]来确定方案Ai在目标Cj下的Vague值。这样不仅克服了以往取值的盲目性和主观性，而且还统一了标准，因为5个指标的含义不同，计算出来的评价值数量级也不同，而采用上述方案可以在Vague值求取中用同一标准将其进行了归一化处理。

对某一种算法，要考虑它在一个评价指标下是否满足决策者的需求，就必须确定决策者能够接受的满意值和不满意值的范围，这可用目标等级来表示。

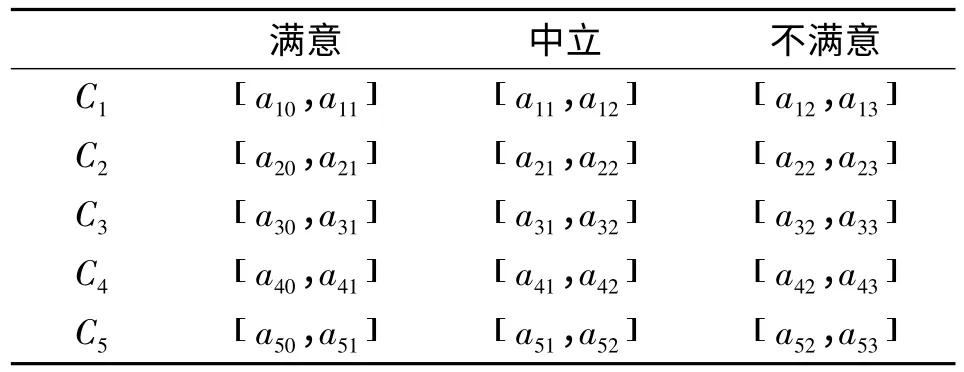
表1 目标等级表

设算法Ai在目标Cj下求取的值为xij，令:

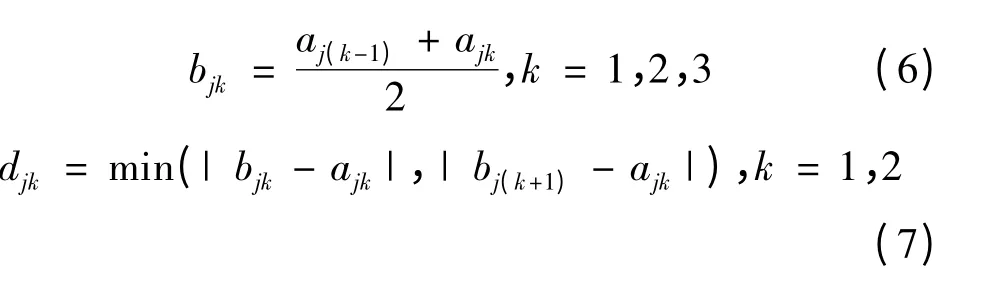
当aj0＜aj1＜aj2＜aj3时:

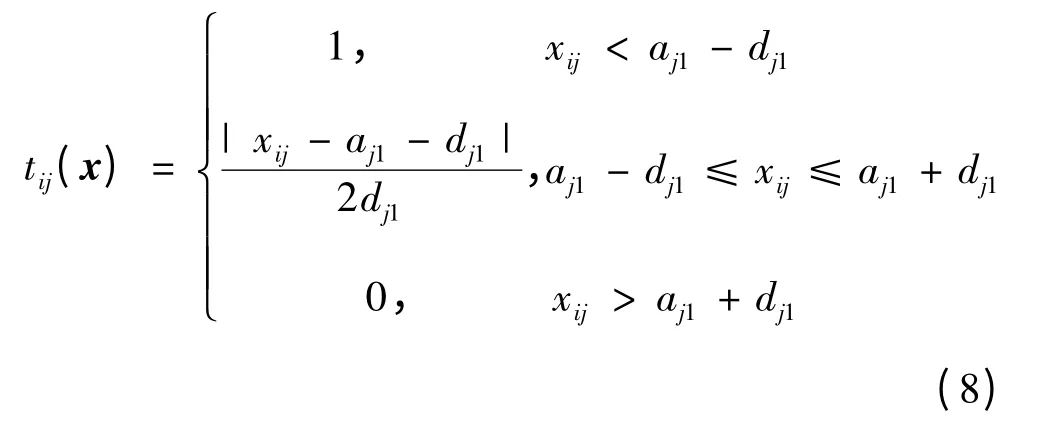
当aj0＞aj1＞aj2＞aj3时:

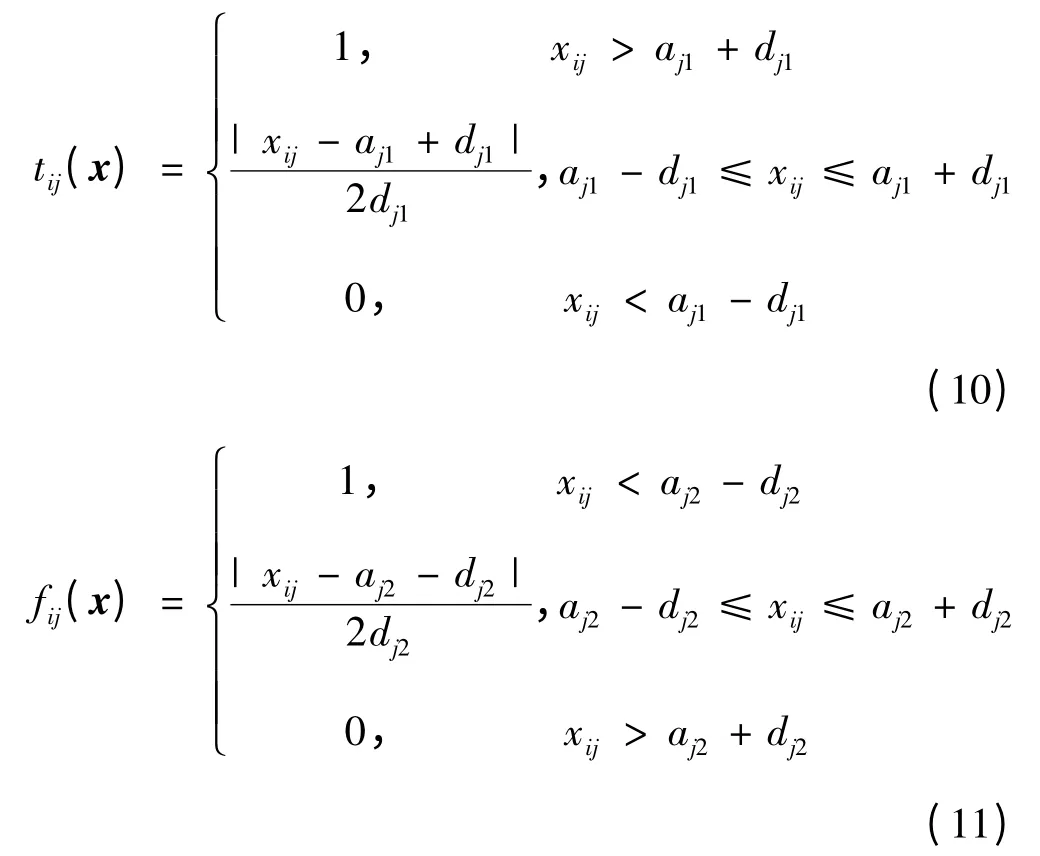
由以上公式计算出真隶属度函数、假隶属度函数和犹豫度函数后就可确定出目标的Vague值。

2.3 Vague值转化为模糊值

Vague集是由模糊集发展而来的，其本质还是模糊集。因此，可以利用某种方式将Vague集转换成Fuzzy集，然后再进行决策。

还是以选举模型为例，给定一个Vague值为[0.5，0.8]，有学者研究时提出将犹豫隶属度赋值为0.5，真隶属度赋值为1，假隶属度赋值为0，由此，得到转化后的模糊值为 0.5+0.3 × 0.5+0.2 × 0=0.65。这种方法处理问题看起来也能达到一定的效果，但是，在对具体问题描述时可能会丢失掉一些信息。原因是没有考虑其他赞成或反对的人对他们的影响。不难设想，当支持的人比反对的人多时，中立的人有投支持票的倾向;当支持的为零时，中立的人也不会全部改投反对;但不是所有的中立者都有支持哪一方的倾向，他们有坚持自己意见的可能。对于组合导航系统来说，也是如此，它是一个有机统一的整体，一部分的性能改变就很可能影响其他部分性能的变化。

基于以上论述，文中按以下公式将Vague值转化为模糊值，并由此构建模糊矩阵F:

当tij=0时:

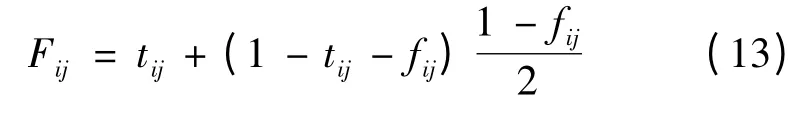
当fij=0时:

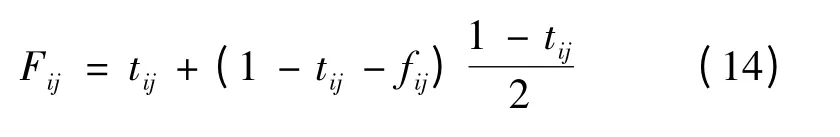
2.4 构造模糊值线性序

基于Vague值和模糊值矩阵对各方案进行排序规则如下:

如果Fi1k＞Fi2k，则Ai1排在Ai2之前;

如果 Fi1k=Fi2k、ti1k＞ ti2k，则 Ai1排在 Ai2之前;

如果Fi1k=Fi2k、ti1k=ti2k、1 － fi1k＞ 1 － fi2k，则Ai1排在Ai2之前;

如果 Fi1k=Fi2k、ti1k=ti2k、1 － fi1k=1 － fi2k，则 Ai1和Ai2地位相同。

由此构造出各个指标对应的组合导航信息融合算法的排序。分别记为:L1，L2，…，Ln。

2.5 构造评判矩阵

5 个指标的权重分别为 ω1、ω2、ω3、ω4、ω5，权重的确定方法分为主观法、客观法和组合权重法3种。文中将专家赋值法和熵权法有机的结合起来确定权重系数。具体步骤如下:

1)由m种算法对5项指标构成的矩阵x，xij表示算法 j对指标 i的指标值;i=1，2，…，5;j=1，2，…，m。

由于各指标的量纲不一致，所以首先必须将决策矩阵进行归一化处理。

2)计算熵值

第i个指标的熵定义为:

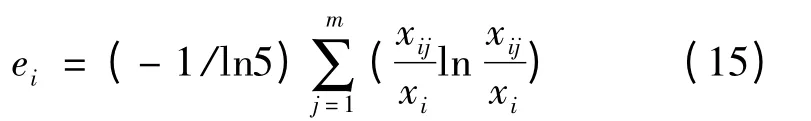
3)确定客观权重

4)利用专家赋值法确定各指标在评价中的主观权重系数hi。

5)计算组合权重

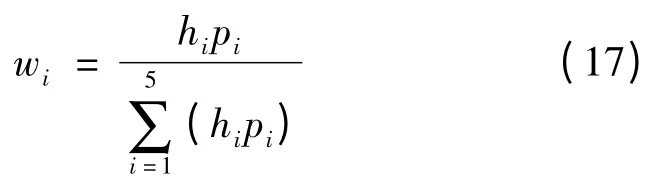
由此构造评判矩阵R:

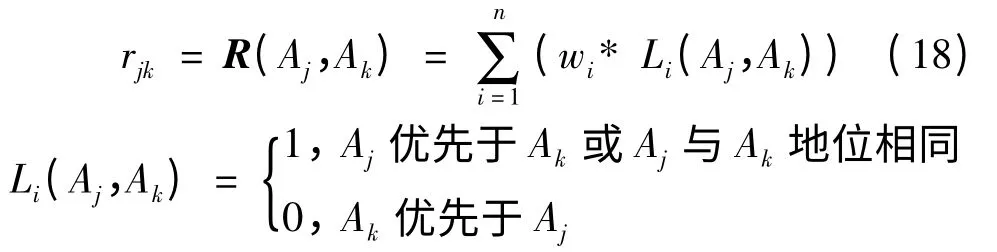
其中rii=0。

2.6 方案排序

对评判矩阵R矩阵每一行的元素求和:

Mi值最大的就是最优评估算法。

3 实例结果及性能分析

利用已建立的算法评价指标及Vague评判方法对INS/GPS/SAR组合导航信息融合算法品质进行评估。

实验步骤:

1)飞行轨迹及飞行参数设定如表2所示。

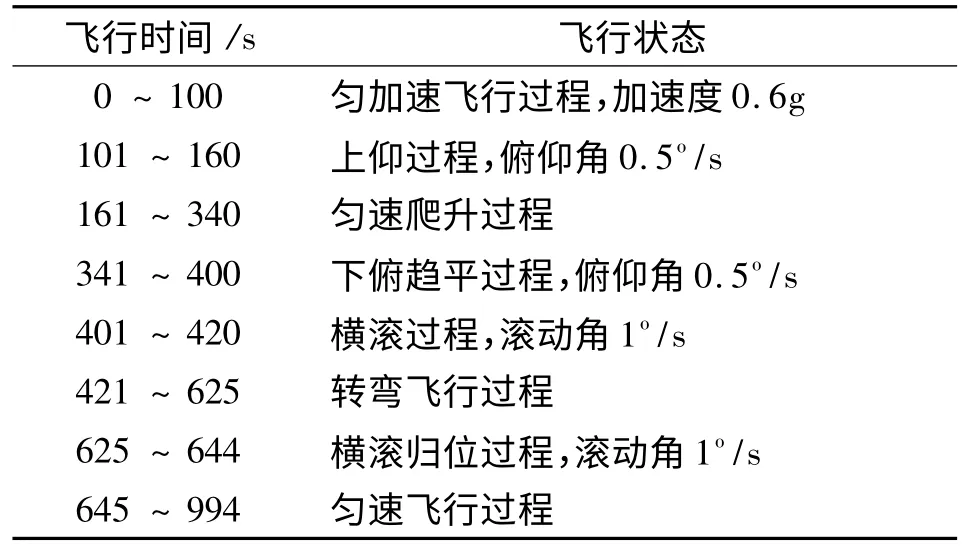
表2 飞行轨迹

2)选取滤波方法

文中采用标准Kalman滤波算法和Sage-Husa自适应滤波算法进行组合导航解算。

3)性能指标的求取

基于上述分析，依据式(1)～式(5)计算两种滤波算法在正常情况和人为设定野值情况下的量化值如表3所示。

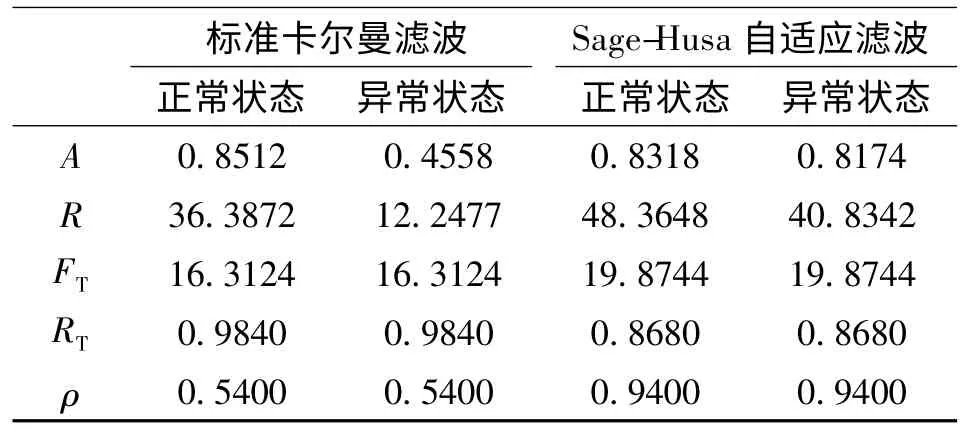
表3 性能指标量化值

4)Vague值的求取

由表3可以确定目标等级划分如表4所示。

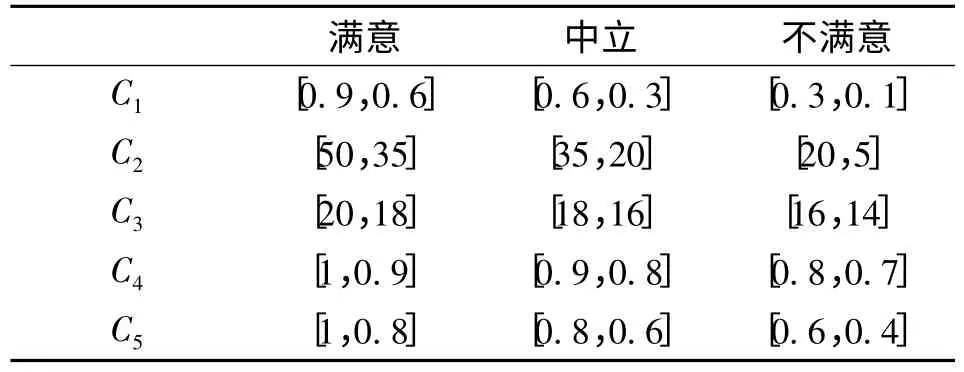
表4 目标等级划分

由式(6)、式(7)可得:

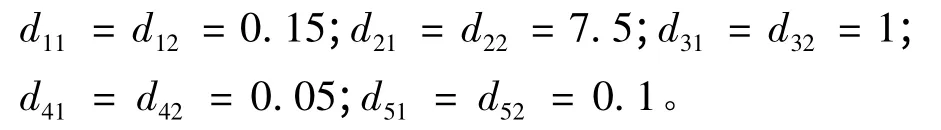
由式(10)、式(11)可得Vague集表示如下:

5)模糊值矩阵F计算

由式(12)～式(14)计算可得:

6)对模糊值F中的每一列数值大小进行排序

L1(按指标C1排序):A1A3A4A2

L2(按指标C2排序):A3A4A1A2

L3(按指标C3排序):(A3A4)(A1A2)

L4(按指标C4排序):(A1A2)(A3A4)

L5(按指标C5排序):(A3A4)(A1A2)

括号内的元素表示在相应指标下的地位相同。

7)最优评估算法的确定

专家赋值法给出的主观权重为:

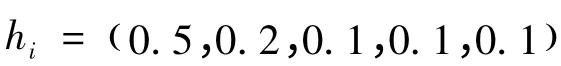
由式(17)、式(18)计算得到的客观权重为:

由式(19)计算得到的组合权重为:

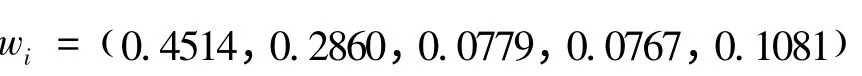
所以计算模糊评判矩阵R为:

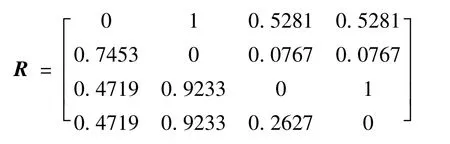
从R矩阵中可以得到，各种算法求和评价结果如表5所示。

表5 性能评估结果

从评估结果上可以看出，正常状态下的Sage-Husa自适应滤波算法的性能最优。

从算法求解的过程和结果来看，文中所提出的评估方法有以下几点改进:

1)所建立和完善的评估指标比较科学全面的反映了数据融合算法的性能，从表3可以看出，标准卡尔曼滤波在鲁棒性、容错性和诊断率方面差于Sage-Husa自适应滤波，这是显而易见的，因为Sage-Husa自适应滤波引入了自调节性能，它最基本、最主要的性质就是根据外界的变化，采用一种有序的搜索过程，在一类允许的可能范围内不断地寻找最佳值，从而不断的改进滤波，有效克服滤波的发散。所以它的的稳定性和可靠性要优于标准卡尔曼滤波。标准卡尔曼滤波在实时性方面优于Sage-Husa自适应滤波，这是由于Sage-Husa自适应滤波增加了滤波的步骤和复杂程度。

2)Vague值的求取合理且简单明了，引入了一种求取不明确系统Vague值的方法，克服了以往专家打分系统给值或者经验赋值的片面性和复杂度。

3)全面细致的分析了模糊值转化的标准和原则，建立的转化公式合理可行。

4)增加了模糊值线性序排序中所有取值一致情况下的排序原则。

5)由熵权法从建立的指标体系值中得到客观权重，并与专家赋值法得到的主观权重组合得到各指标的较为客观的组合权重。

4 结束语

针对组合导航信息融合算法的不断增多，文中就如何对算法品质进行评估，首先在文献[1]的基础上提出了一套完备的指标体系，即:滤波精度、实时性、鲁棒性、容错性和诊断率。并给出了各指标的数学定义式。同时，首次将Vague集理论引入组合导航信息融合算法品质评估中，并提出了一种改进的Vague集多指标决策模糊值线性序法。最后，通过两种常用算法在正常状态和异常状态下的评估实验可知，改进的Vague集理论模型克服了Vague值靠经验获取和权重依专家赋值的随意性，对组合导航数据融合算法评价有一定的指导意义和应用价值。

[1]刘勇志，贾兴亮，刘丙杰.一种组合导航滤波性能评估算法[J].弹箭与制导学报，2008，28(5):45 －47.

[2]要瑞璞.捷联式惯性导航系统性能综合评价新方法[J].计算机仿真，2005(2):48－50.

[3]姜兴宇，王贵和，张新敏.面向全生命周期的产品质量综合评价方法研究[J].系统仿真学报，2009，20(20):5581－5584.

[4]要瑞璞，沈惠璋.模糊模式识别在导航系统性能综合评价中的应用研究[J].舰船科学技术，2009，31(2):97－99.

[5]Gau W L，Buehrer D J.Vague sets[J].IEEE Trans.Systems Man and Cybernetic，1993，23(2):610 －614.

[6]Huang Kuo-chen，Yang G K.An enhanced method and its application for fuzzy multi-criteria decision making based on vague sets[J].Computer-Aided Design，2008，40(4):447－454.

[7]Wang Ying-ming.Multiple attribute decision making based on fuzzy preference information on alternatives Ranking and weighting[J].Fuzzy Sets and Systems，2005，153(3):331－346.

[8]Ye Jun.Improved method of multicriteria fuzzy decision making based on vague sets[J].Computer-Aided Design，2007，39:164 －169.

[9]Gau Wen-Lung，Daniel J.Vague sets[J].IEEE Transactions on Systems，Man，and Cybernetics，1993，23(2):610－614.

[10]Hong D H，Choi C H.Multicriteria fuzzy decision making problems based on vague set theory[J].Fuzzy Sets and Systems，2000，114(1):103 －113.

[11]要瑞璞，沈惠璋.Vague集多指标决策的模糊值线性序法[J].计算机工程与应用，2009，45(28):39－40.

[12]程乾生.质量评价的属性数学模型和模糊数学模型[J].数理统计与管理，1997，16(6):18 －23.