装配式防屈曲支撑设计理论的研究进展
郭彦林,张博浩,王小安,姜子钦
(清华大学 土木工程系,北京 100084)
0 引 言
普通钢支撑在往复水平地震作用下,容易发生受压屈曲而导致刚度、承载力和耗能能力的急剧下降,显著降低结构的延性。防屈曲支撑(Bucklingrestrained Brace,BRB)通过在内核构件的外围设置约束构件抑制其受压屈曲,在小震作用下提供稳定的侧向刚度,在中震或大震作用下内核受拉、受压均能全截面进入屈服,荷载-位移滞回曲线饱满,因此是一种兼具抗侧承载力与耗能能力的消能减震构件。
1994年美国北岭地震和1995年日本阪神地震后,防屈曲支撑开始用于工程实践,在日本、美国和中国台湾等地得到广泛应用。中国大陆地区从2000年建成北京威盛大厦开始,也逐渐尝试该类构件。防屈曲支撑可以广泛应用于高层或中低层框架结构、网架网壳等大跨结构以及桥梁结构中,既可用于新建建筑,又可用于已建建筑的加固改造和震后修复。
防屈曲支撑主要由内核构件与外围约束构件组成。内核构件一般采用低屈服点高延性的钢板或热轧型钢或组合焊接构件,直接承受轴向荷载作用;外围约束构件主要承受内核侧向变形引起的弯矩,并不直接承受轴力。内核构件与外围约束构件之间在纵向和横向应留有适当间隙,并用无粘结材料隔离,防止支撑受压时内核与外围约束构件发生纵向接触或由于内核钢材泊松效应引起横向接触,这种接触将导致外围约束构件也承受部分轴力,使外围约束构件提前破坏或内核强度超过预期值,对框架产生不利影响。
防屈曲支撑构件的种类较多,根据外围约束构件的材料划分,主要有3种类型,即混凝土约束型、钢管混凝土约束型和全钢约束型;根据外围约束构件的组成方式,防屈曲支撑可分为整体式和装配式。
混凝土约束型和钢管混凝土约束型防屈曲支撑的外围约束构件一般为整体式,混凝土现场湿作业工作量大,混凝土和内核钢板间的精度较难控制,如果工程需要设计大吨位与超长防屈曲构件,采用整体式防屈曲支撑必将给运输与安装带来较大的难度。装配式防屈曲支撑(Assembled Buckling-restrained Brace,ABRB)的外围约束构件通常由型钢或钢板通过螺栓装配组成,精度容易控制,现场安装方便,地震后仅需更换屈服的内核,外围约束构件可实现重复利用,并且型钢和钢板在中国来源广泛,可实现截面形式的多样化。
1 装配式防屈曲支撑的截面形式
装配式防屈曲支撑的内核一般采用一字形或十字形截面,也可采用H型截面。内核沿纵向可分为核心段、过渡段和连接段(图1),核心段是中部较长的一段区域,也是地震时屈服耗能的主要工作部分,全长被外围构件约束;连接段是内核两端与框架节点板相连接的区域,未被外围构件包裹,由于螺栓孔削弱及缺少外围构件的可靠约束,其截面尺寸应大于核心段,以保证强度和稳定性要求;过渡段是核心段向连接段过渡的区域,与连接段相接部分暴露在外围约束构件外,而与核心段相接部分则被包裹在外围约束构件内部,为保证其在弹性阶段工作,可焊接加劲肋或增加截面宽度等,但截面转变应尽量平缓以避免应力集中。

图1 装配式防屈曲支撑内核构件的纵向组成Fig.1 Profile of Core Component in ABRB
2003年Tsai等[1]提出了双内核双套筒约束型装配式防屈曲支撑(图2),钢管通过连接板焊接组成,套筒中的偏心内插1片内核构件,2个套筒之间通过螺栓连接。防屈曲支撑与框架的连接,只需用2个内核板夹住框架连接板即可,有效地解决了传统防屈曲支撑需要设置拼接板与框架连接而造成连接长度大、螺栓多、有效约束区短等问题。
2006年Tremblay等[2]提出了方钢管约束型装配式防屈曲支撑(图3)。方钢管焊接在连接板上组成外围约束构件,一字形内核两侧的外围约束构件通过连接板上的若干组螺栓连接。2个连接板之间填充连续的垫板和填隙板以保证内核和外围约束构件之间存在合理间隙。在内核连接段,焊接竖向加劲肋形成十字形截面以保证其强度和稳定性。
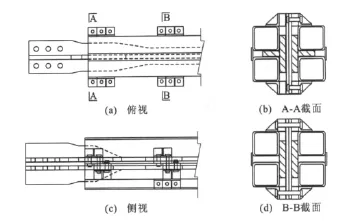
图2 双内核双套筒约束型装配式防屈曲支撑Fig.2 ABRB Restrained by Double Core and Double-tube

图3 方钢管约束型装配式防屈曲支撑Fig.3 ABRB Restrained by Square Steel Tubes
2008年Usami等[3]提出了一种一字形内核双T型钢约束型装配式防屈曲支撑(图4),内核构件四周设置无粘结材料。
2010年郭彦林等[4]提出了多种新型全钢装配式防屈曲支撑。内核为一字形板时,可通过2个有外伸钢板带的方矩管对扣约束[图5(a)],也可通过4个槽钢组合约束[图5(b)],或通过2个槽钢与1个工字形钢组合约束[图5(c)]。内核为十字形板时,可通过4个角钢捆绑约束[图5(d)]或4个方矩管捆绑约束[图5(e)],方矩管可由2个尺寸不同的等边角钢对焊或由4个钢板焊接组成,采用四角钢约束时沿支撑纵向在角钢内侧应布置若干加劲肋以提高约束构件的刚度和抗畸变能力。内核为H型钢时,外围约束构件由2个方矩管和2个钢板组成[图5(f)],钢板也可用方矩管替代。内核与外围约束构件的接触面上,可粘贴硬质橡胶以减小二者之间的摩擦,外围不同构件之间的距离可通过螺栓处的垫块厚度进行调整。
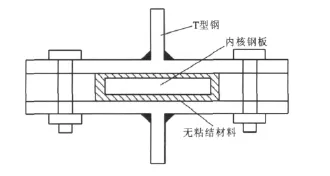
图4 双T型钢约束型装配式防屈曲支撑Fig.4 ABRB Restrained by Double T-rods

图5 若干种新型全钢装配式防屈曲支撑Fig.5 Several Novel Types of All-steel ABRB
2010年郭彦林等[5]提出了双矩管带肋约束型装配式防屈曲支撑(图6),内核为热轧H型钢,外围约束构件由2个带肋的矩形钢管通过长螺杆连接件扣压在H型钢腹板两侧组成,带肋的矩形钢管由在冷弯空心型钢或冷弯薄壁型钢矩形管上焊接槽形加劲肋形成。为了提高外围部分的刚度和承载力,钢管内可浇灌混凝土。为保证内核与外围约束构件沿轴向单独变形而不互相约束,可在外围约束构件上开设椭圆形螺栓孔。由于H型钢的截面能够保证构件屈服先于局部失稳发生,该支撑可通过加劲肋实现线接触,从而避免外围构件约束内核受压膨胀而导致内核屈服强化。
2010年Chou等[6]提出的一字形内核装配式防屈曲支撑与图5(a)类似,外围约束构件由平钢板和槽钢焊接组成,并在内部浇灌混凝土。
2012年Genna等[7-8]提出了一种一字形内核双槽钢约束型装配式防屈曲支撑(图7),组成外围约束构件的槽钢需要进行精加工。
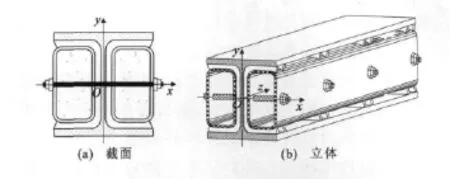
图6 双矩管带肋约束型装配式防屈曲支撑Fig.6 ABRB Restrained by Dual Ribbed Rectangular Tubes
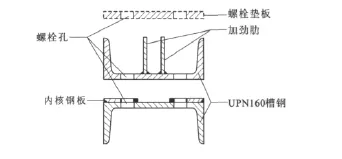
图7 双槽钢约束型装配式防屈曲支撑Fig.7 Double-channel ABRB
2012年Usami等[9]提出了铝合金装配式防屈曲支撑[图8(a)],铝合金密度仅为钢材密度的1/3,并且抗腐蚀能力好,容易加工,在桥梁和近海工程中具有良好的应用前景。针对常见的焊接十字形连接段低周疲劳性能较差的问题,提出采用4个角钢经螺栓拼接组成十字形连接段[图8(b)],抗疲劳性能可提高4~5倍。

图8 铝合金装配式防屈曲支撑Fig.8 Aluminum Alloy ABRB
2 外围约束构件的设计
整体式防屈曲支撑的设计主要包括2个方面:①内核构件的确定;②外围约束构件的设计。对于装配式防屈曲支撑而言,外围多个约束单元通过螺栓的“捆绑作用”形成整体参与工作,因此螺栓的强度和布置也是重要的设计内容。
由于内核的截面性质决定了防屈曲支撑构件对整个结构刚度和强度的贡献,所以根据结构计算内力可以确定内核的截面需求。
外围约束构件仅为内核提供侧向约束,不直接承担框架轴力,本质上是一个受弯构件。外围约束构件的尺寸应与内核相匹配,在内核确定后再进行设计,既要保证内核整体屈曲不先于截面屈服发生,又不能过于浪费钢材。
2.1 内核与外围约束构件的相互作用
2.1.1 防屈曲支撑的整体单波形弯曲
江磊鑫[10]假定防屈曲支撑构件存在着初弯曲w0=v0sin(πz/L),其中,v0为构件初弯曲幅值,L为构件长度,z为截面坐标,推导出了内核与外围约束构件之间的挤压力q(z)沿构件长度方向的分布模式(图9),为保持内力的自平衡,内核在支撑两端分别作用一个集中的侧向挤压力Fend。

图9 整体变形模式下内核与外围的受力状态Fig.9 Interaction Between Core and Restraining Components When Core Overall Bends
挤压力q(z)与集中侧向挤压力Fend分别为

式中:Pcr为整根构件的弹性屈曲荷载;P为防屈曲构件承受的轴压力;E2I2为外围部分对自身截面形心轴的抗弯刚度。
2.1.2 内核的整体多波形弯曲
若防屈曲支撑内核的初始几何缺陷为正弦单波分布,内核在轴压力作用下首先发生半波弯曲屈曲,在跨中位置与外围约束构件接触,产生的接触反力限制了内核低阶屈曲模态的发展,使内核发生高阶屈曲形成更多半波数。在波峰或波谷处,内核会对外围约束构件产生集中侧向挤压力。如果外围构件约束能力足够,外荷载可以继续增加直至内核全截面屈服,达到最大轴压力Pmax,如图10所示,其中,g为内核与外围约束构件之间的间隙,e为轴压作用偏心距。
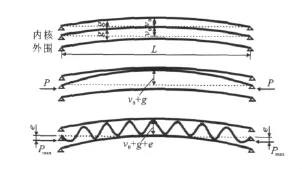
图10 防屈曲支撑整体失稳前的受力状况ig.10Force Behaviors of BRB Before Global Buckling
Wang等[11]将内核简化为承受轴力P0和侧向挤压力F1的两端铰接梁-柱理论模型(图11)。若内核的初始几何缺陷为正弦单波分布,在轴力P1作用下内核在跨中处与外围约束构件接触,对外围约束构件施加侧向挤压力F1。对于一字形内核,根据平衡法可推导得到F1的近似值,即


图11 梁-柱理论模型Fig.11 Beam-column Theoretical Model
其最不利情况可按下式计算
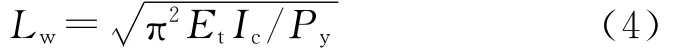
式中:Lw为内核形成多波形变形时的半波长;EtIc为内核绕弱轴的抗弯刚度;Py为内核的屈服轴力。
实际支撑在轴压力P作用下内核发生多波屈曲,变形模式复杂且受初始几何缺陷影响显著,内核对外围约束构件侧向力F的分布与大小难以精确预测,但利用式(3)所得到的侧向挤压力F1可偏保守地估算侧向力F。
文献[8]中考虑了内核非弹性屈曲以及循环加载对侧向挤压力的影响。假定内核形成均匀的多波屈曲,根据Shanley理论,推导得到考虑材料非弹性屈曲后内核对外围侧向挤压力的合力F为

有限元计算结果表明,随着加载圈数的增多,内核波峰处与外围约束构件的接触面积逐渐增大(图12),外围受到的挤压力也逐渐增大,考虑循环加载后的修正公式为

式中:α(n)为循环n圈对应的修正系数,与加载幅值有关,但具体取值仍有待进一步研究。
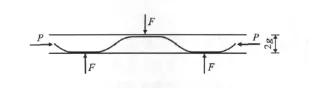
图12 内核与外围接触区域塑性扩展示意Fig.12 Sketch of Bucked Shape in Presence of Flatting of Core at Contact Zones
2.1.3 十字形内核的高阶扭转变形
对于十字形内核的防屈曲支撑,不仅会发生上述的整体单波形弯曲和整体多波形弯曲,如果内核板件宽厚比较大,还会发生高阶扭转变形,如图13所示,其中,bc1,tc分别外伸板件的宽度和厚度。这种扭转变形会对外围约束构件施加侧向集中挤压力FT,该挤压力作用在十字形截面两侧的外伸板件边缘处,且呈跳跃式分布。
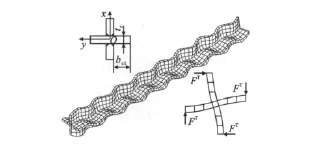
图13 十字形内核构件的扭转变形Fig.13 Torsional Deformation of Cross-shaped Inner Core Component
十字形内核构件扭转变形产生的侧向力作用机理复杂,难以给出明确的计算方法,因此可通过限制内核的板件宽厚比避免扭转变形发生。参考《钢结构设计规范》(GB 50017—2003)[12]中关于双轴对称十字形截面构件扭转屈曲的规定,当十字形内核的外伸板件宽厚比满足式(7)时,内核与外围约束构件之间的相互侧向作用力可仅考虑整体单波形变形与整体多波形变形的影响。规范中宽厚比的要求为
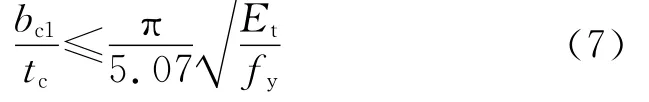
式中:fy为内核构件的屈服强度。
2.2 外围约束构件刚度的确定
2.2.1 钢管混凝土约束型防屈曲支撑
在钢管混凝土约束型防屈曲支撑中,钢管混凝土作为一个纯弯构件,应考虑混凝土开裂造成的外围约束构件抗弯刚度的折减。目前,对钢管混凝土抗弯刚度的计算有多种方法,所得结果存在较大的差异[13]。
日本规范AIJ 1997[14]中规定抗弯刚度EI为
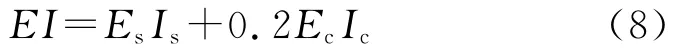
式中:Es,Ec分别为钢管和混凝土的弹性模量;Is,Ic分别为钢管和混凝土的截面惯性矩。
英国规范BS 5400:2005[15]中规定钢管混凝土抗弯刚度K为

欧洲规范ENV 1994 1-1:2004[16]中规定
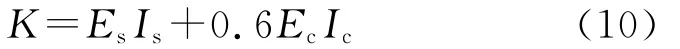
美国规范 AISC LRFD:2005[17]中规定
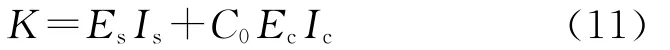
式中:C0为系数,C0=0.6+2α≤0.9,α为钢管截面面积As与钢管混凝土总截面面积Asc之比。
《钢管混凝土结构技术规程》(DBJ 13-51—2003)[18]中规定

式中:a为与钢管截面形状有关的系数,对于方形、矩形钢管混凝土,a取0.6,考虑到圆钢管对核心混凝土的约束效果更好,对抗弯刚度的折减可略小,系数a取0.8。
2.2.2 装配式防屈曲支撑
整体式防屈曲支撑外围构件的约束刚度较为明确,但装配式防屈曲支撑的外围约束构件仅依靠有限数目的螺栓连接,因此其约束刚度的计算比整体式外围约束构件更为复杂。
郭彦林等[19]针对如图5(d)所示的四角钢约束型装配式防屈曲支撑,提出了如图14所示的悬臂空腹桁架简化模型,其中,Fe为端部承受的集中力,EI1,A1分别为单个角钢绕与其板件平行的主轴的抗弯刚度和截面面积,EI2为角钢间的连系刚度,h为上组角钢与下组角钢各自形心轴之间的距离。采用力法计算外围约束构件在侧向挤压力作用下的变形,进而得到其约束刚度。
2.3 防屈曲支撑的整体设计方法
2.3.1 强度要求
Takahashi等[20]针对钢筋混凝土约束型防屈曲支撑,提出了外围约束构件的设计应保证构件的轴压弹性屈曲荷载Pcr不小于内核的屈服轴力Py,即

图14 外围约束构件的简化桁架模型Fig.14 Simplified Truss Model for Outer Restraining Component
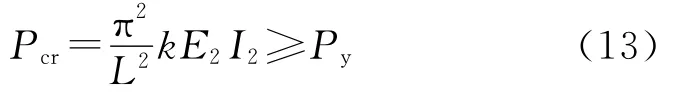
式中:k为钢筋混凝土考虑开裂后的刚度折减系数。
考虑到内核屈服后其刚度折减很多,式(13)中Pcr的计算偏保守地忽略了内核的刚度贡献。
Fujimoto等[21]将防屈曲支撑整体弹性屈曲荷载Pcr与内核的全截面屈服轴力Py之比定义为“约束比”,根据支撑整体失稳前外围约束构件不发生边缘屈服的条件,并考虑内核初始几何缺陷的影响,推导出约束比ζ的限值,即

式中:E2为外围约束构件材料的弹性模量;fy2为外围约束构件的屈服应力。
针对钢管混凝土约束型防屈曲支撑的数值计算结果,建议实际设计中约束比ζ大于1.5。
文献[3]中假定内核发生多波屈曲后,对外围的侧向挤压力沿构件长度方向均匀分布,推导出构件整体屈曲时对应的最大轴压力Pmax,并定义构件安全系数vF为最大轴压力Pmax与内核屈服轴力Py之比,即

式中:PE2为外围约束构件的弹性屈曲荷载;My2为外围约束构件的屈服弯矩。
试验结果表明,当构件安全系数vF达到3时,防屈曲支撑的延性比可在20以上。
文献[10]中根据如图9所示的内核与外围约束构件相互作用,推导出当荷载达到内核屈服轴力Py时,外围约束构件跨中最大弯矩Mmax为
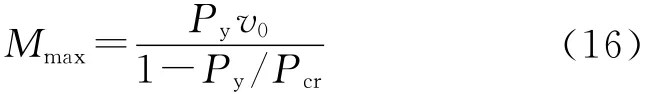
根据外围约束构件边缘纤维不发生屈服的条件,可得到约束比ζ满足
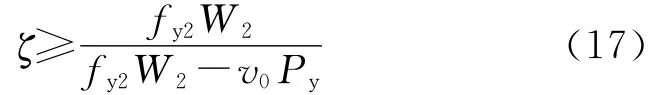
式中:W2为外围约束构件的截面模量。
实际支撑中,内核与外围约束构件之间一般预留一定的间隙,设单侧间隙大小为g,若考虑间隙对支撑整体受力性能的影响,则式(17)中应用v0+g代替v0。
需要注意的是,式(17)中没有考虑内核钢材屈服强化所导致的荷载增加,也没有考虑装配式防屈曲支撑的外围约束构件在螺栓附近的应力集中现象。考虑钢材屈服后强化,内核的受压极限承载力Pu可以表示为[22-23]

式中:Ry为钢材实际屈服强度与屈服强度标准值之比;ω为应变强化调整系数,反映了钢材屈服后的强化程度;β为抗压强度调整系数,即防屈曲支撑受压承载力与受拉承载力之比,是一个大于1的系数。
拉压不对称的原因主要有[24]:支撑受压时内核与外围约束构件之间相互作用复杂,二者之间可能存在摩擦,内核受压膨胀而导致截面增大,并可能受到外围构件约束而产生三轴应力,以上各参数可通过试验测得[25]。另一方面,引入修正系数η来考虑外围螺栓局部应力集中可能引发的稳定极限承载力降低,η的取值与截面类型、螺栓布置方式等因素有关。因此,通过考虑钢材屈服后强化和螺栓集中力作用等进行修正,得到约束比ζ的限值为
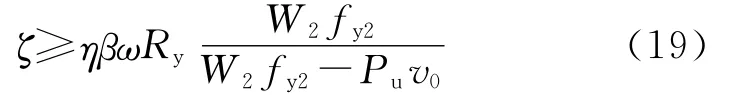
文献[6]中针对一字形内核装配式防屈曲支撑的试验和有限元研究表明,当防屈曲支撑构件的约束比ζ大于2时,由于内核屈服后强化,防屈曲支撑可以承受1.4~1.5倍的内核屈服轴力,此时支撑仍未发生整体失稳。
综上所述,内核构件截面确定后,外围约束构件的设计可归结为一个重要参数即约束比ζ的确定,约束比ζ的取值应保证支撑的整体失稳荷载不小于内核的屈服轴力。该方法使用简便,目前已被很多学者采用。
2.3.2 受压延性与累积塑性变形能力
防屈曲支撑在地震下承受反复荷载作用,内核屈服后滞回消耗地震能量,因此防屈曲支撑的延性应满足一定要求。定义受压延性系数峰值μmax和累积塑性变形能力系数μc分别为

式中:Δmax为支撑最大轴向位移;Δby为支撑屈服轴向位移;Δp为支撑塑性轴向位移。
μmax反映了支撑在破坏前的最大受压变形能力,而μc反映了破坏前支撑往复累积塑性变形的能力。AISC 341-05中规定防屈曲支撑的累积塑性变形能力系数应满足μc≥200,而FEMA 450[26]中规定μc≥140。
为使防屈曲支撑的累积塑性变形能力达到设计要求,保证地震反复荷载作用下内核不提前发生断裂破坏,防屈曲支撑的内核应选用延性较好的低屈服点钢材,同时外围约束构件应具备足够的刚度。Iwata等[27]针对钢管混凝土约束型防屈曲支撑的试验结果表明,累积塑性变形能力系数μc=75ζ,由此可得,防屈曲支撑应满足ζ≥2.67(AISC 341-05)或ζ≥1.87(FEMA 450)。
3 螺栓连接的设计
与外围整体式防屈曲支撑不同,装配式防屈曲支撑的多个外围约束单元通过螺栓连接组成外围约束构件,螺栓的“捆绑作用”保证外围约束构件整体协同工作并为内核提供必要约束。
“捆绑作用”分为2个部分:一是使各外围约束单元作为整体共同工作,满足平截面假定,抑制约束单元之间的纵向相互错动,此时螺栓承担沿构件长度方向的剪力作用;二是将内核对外围部分的作用力在各外围约束单元之间进行分配和传递,保证各约束单元的侧向变形协调,此时螺栓承担拉力作用。
因此,螺栓连接是装配式防屈曲支撑构件特有的重要设计内容,主要包括:螺栓强度的验算和螺栓间距的控制。
3.1 螺栓强度的验算
文献[6]中针对一字形板内核装配式防屈曲支撑,假定外围约束构件为刚性,认为所有螺栓拉力之和等于内核对外围约束构件的挤压力之和,局部最大挤压力F使外围约束构件形成塑性铰,即

式中:Mp为外围约束构件的塑性铰弯矩。
该方法认为螺栓仅受拉力作用,但实际上支撑发生整体弯曲时,螺栓还承担不同外围约束单元之间纵向错动引起的剪力。图15为内核构件的高阶多波屈曲。
文献[7],[8]中针对如图7所示的双槽钢约束型装配式防屈曲支撑,通过试验实际测量了支撑工作过程中螺栓的受力情况,并建立了简化的有限元平面模型。试验结果表明:在不同加载圈数,螺栓拉力变化很大且对屈曲半波数非常敏感;内核与外围之间的间隙尺寸对螺栓拉力也有显著影响。有限元计算所得的轴向荷载-位移曲线与试验曲线吻合良好;螺栓受力与试验数据变化趋势吻合,但具体数值存在一定偏差;屈曲半波数变化时,螺栓拉力会产生突变。可见,由于屈曲半波数受构件缺陷、摩擦等因素影响较大,精确的螺栓拉力值难以得到。但根据式(6)求得的内核对外围侧向的挤压力,并考虑内核与外围之间摩擦力的影响,得到的螺栓拉力估计值可以满足工程的安全要求。
文献[4]中针对如图5(b)所示的四槽钢约束型防屈曲支撑,研究了螺栓对外围约束构件的“捆绑作用”,螺栓承担的最大剪力[图16(a)]位于构件的两端,而最大拉力[图16(b)]位于构件的跨中和两端。对于防屈曲支撑绕强轴弯曲的情况,螺栓剪力可由截面弯矩变化的不平衡正应力求得,内核屈服时的端部螺栓最大剪力FxQ1,end为

图15 内核构件的高阶多波屈曲Fig.15 High-mode Multi-wave Buckling of Inner Core Component

式中:Sud为上槽钢或下槽钢对总截面形心轴的静矩;Pcr,2为外围构件的弹性屈曲荷载;s为螺栓间距;Ix为外围部分绕强轴的惯性矩。

图16 绕强轴弯曲时的螺栓强度验算Fig.16 Strength Verifications of Bolts Around Strong Axis Bending
3.2 螺栓间距的控制
在装配式防屈曲支撑中,螺栓除了满足强度要求之外,其数目及间距也必须满足一定要求。如果螺栓间距太大,螺栓间的单个约束单元可能承担较大的内核多波屈曲时的侧向挤压力,在外荷载达到内核屈服轴力Py之前发生局部弯曲变形;如果螺栓间距太小,可能给施工造成困难。
螺栓的最小间距可以按照《钢结构设计规范》(GB 50017—2003)中的构造要求,保证施工的顺利进行和结构的安全工作。
文献[4]中针对如图5(b)所示的四槽钢约束型防屈曲支撑,定义螺栓间的约束比ζs为螺栓间单个槽钢的弹性屈曲荷载Pcr,s与内核屈服轴力Py之比,参考整体约束比的计算方法,得到避免螺栓间局部弯曲失稳的螺栓最大间距为
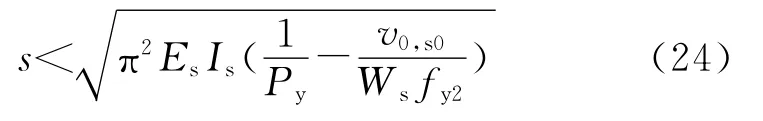
式中:Ws为单个约束单元对自身形心轴的抵抗矩;v0,s0取螺栓间距的1/1 000。
4 防屈曲支撑端部节点
在工程应用中,防屈曲支撑的端部可以通过销轴与主体结构相连,形成铰接节点,也可以通过高强度螺栓或焊接与主体结构相连,形成刚接节点,如图17所示。
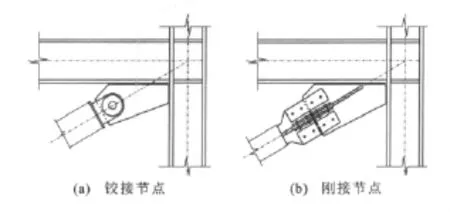
图17 防屈曲支撑的节点形式Fig.17 Connection Types for BRB
在防屈曲支撑中,由于内核压缩后要缩短,内核总是长于外围约束构件,内核外伸段由于缺少外围构件的侧向约束,自身稳定性能较差。因此,在设计中对内核外伸段的承载力应予以关注。另一方面,内核外伸段受力行为对防屈曲支撑整体受力性能也有影响,如外伸段转动变形可能导致支撑端部承受附加弯矩,但目前已有的防屈曲支撑整体稳定设计方法仅考虑内核与外围约束构件之间的相互作用,没有考虑端部转动的影响。此外,主体框架一般通过节点板与防屈曲支撑连接,节点板的设计应保证足够的强度和稳定性,以避免提前破坏。
4.1 内核外伸段的稳定性能
Narihara等[28]进行了两端铰接的十字形内核四钢管约束型防屈曲支撑试验。试验结果表明,内核外伸过渡段截面面积扩大到屈服段的1.36倍时,仍会发生平面内压弯屈曲破坏。
Ju等[29]进行了H型钢内核及外围方钢管约束型防屈曲支撑的拟静力试验,采用单向铰支座。试验结果表明,当内核外伸段较长时,端部转动后产生加载偏心距,使内核外伸段的受力状态由受压为主转变为压弯复合受力,支撑端部发生绕弱轴的局部压弯破坏。对于试验采用的100mm×100mm×6mm×8mm的H型内核,当内核外伸段长度超过200mm时应该采取加强措施,如在内核外伸段的翼缘上焊接加强钢板(图18),增大内核外伸段的翼缘宽度。
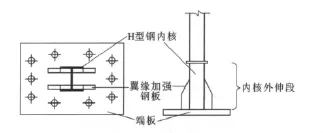
图18 内核外伸段的加强措施Fig.18 Welding of Cover Plate for Reinforcement
赵俊贤等[30]对一种全角钢防屈曲支撑进行了试验研究。当防屈曲支撑两端固接时,耗能发展最为充分;当两端铰接时,由于内核外伸段提前发生局部压弯破坏,耗能能力不能充分发挥;在端部设置转动约束构件能有效限制端部转角,避免内核外伸段发生局部压弯破坏。试验结果表明,当支撑两端铰接且无转动约束构件时,内核外伸段等效截面面积设计为屈服段截面面积的2倍左右,仍不能保证内核外伸段的安全。
对于一字形和十字形的内核,连接段一般为局部加强的十字形截面短柱,其扭转屈曲荷载一般小于其弯曲屈曲荷载,因此更易发生扭转屈曲。Timoshenko等[31]推导出了十字形柱弹性扭转屈曲荷载 的 经 典 解,在 这 之 后 Stowell[32],Bleich[33],Makris[34]研究了十字形柱弹塑性扭转屈曲荷载。Black等[35]针对十字形内核防屈曲支撑的试验表明:文献[34]中采用塑性增量理论推导的弹塑性扭转屈曲荷载σcr[式(25)]与试验结果更为吻合。文献[35]的试验中构件内核外伸段的宽厚比为5,外伸段未发生扭转破坏。

式中:l,b,t分别为内核十字形截面单个板件的长度、宽度和厚度;σy为内核的屈服应力。
4.2 内核外伸段对BRB整体性能的影响
Tsai等[36-37]在中国台湾国立地震工程研究中心进行了三层三跨的足尺寸CFT/BRB框架拟动力试验。试验结果表明,框架中的防屈曲支撑累计塑性变形能力小于单独承力的防屈曲支撑,可能归咎于刚性连接导致的附加弯矩。螺栓连接方式会使支撑端部节点跟随框架梁柱节点发生刚性转动,试验中对转动量进行测量并给出了转角预测公式。
Usami等[38]针对两端铰接的H型内核方钢管约束型防屈曲支撑,采用变刚度的梁模型(图19),利用内核与外围约束构件在交界处的变形协调条件,推导出了交界处的弯矩计算公式。

图19 变刚度的梁模型Fig.19 Variable Stiffness Beam Model
Zhao等[39]通过试验研究了端部转动对两端铰接全角钢型防屈曲支撑性能的影响。试验结果表明:①防屈曲支撑存在C型(2个端部反向转动)和S型(2个端部同向转动)2种转动模式,如图20(a)所示,其中,eu,eb分别为两端轴力作用偏心距,δ为内核轴向变形,θu,θb分别为两端转角,Lo,Lpu,Lpb,Lcb,Lcu,Ly均为长度,实际发生何种转动模式与初始几何缺陷分布有关,文献[37]进行的框架试验中也观察到这2种转动模式;②内核屈服前支撑端部转角较小,内核屈服后转角明显增大,且C型转动模式的转角明显大于S型,由于端部转动将产生附加弯矩,C型转动模式对防屈曲支撑的整体稳定以及端部连接强度更为不利。
考虑端部转动的影响,两端铰接的防屈曲支撑约束比为1.5时,仍会发生整体弯曲失稳。假定外围约束构件和连接段为刚性材料,并忽略内核外伸段的自身弯曲变形,可以建立塑性铰破坏模型[图20(b)],其中,θr,θp分别为刚体和塑性变形引起的转角。根据几何关系推导得到支撑端部的附加弯矩Mup,Mlow分别为

如果防屈曲支撑与框架通过铰接节点相连,内核塑性铰的出现使支撑形成机构,无法继续承担荷载,因此在防屈曲支撑两端一般对内核构件进行外扩处理形成加强连接段。为避免内核外伸段形成塑性铰而破坏,建议在外围约束构件内部即完成内核构件的加强处理,在形成加强连接段后再伸出外围约束构件。
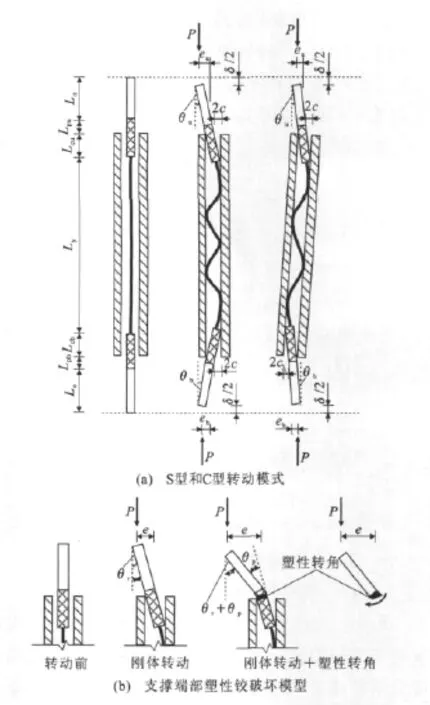
图20 防屈曲支撑端部的转动模式Fig.20 Rotation Modes for BRB Ends
4.3 防屈曲支撑与主体框架的连接构造
目前,各国学者已经进行了一些防屈曲支撑框架试验,其中防屈曲支撑与主体框架的连接构造是这些研究的重点之一,如节点板的面外稳定性、螺栓连接疲劳性能等。
文献[37]中进行了足尺寸CFT/BRB框架拟动力试验,对防屈曲支撑端部节点的性能进行了研究。试验结果表明,在节点板周围自由边上增设加劲肋可有效增强其面外稳定性。对于不设置加劲肋的节点板,其稳定性计算简图如图21(a)所示,弹性屈曲荷载Pcr为

式中:be,Lc均为加劲肋的尺寸参数,Lc=max(L1,L2,L3),L1,L2,L3均为长度(图21);r为最不利截面的回转半径;K′为有效长度系数。
对于防屈曲支撑框架,由于防屈曲支撑端部无约束段刚度弱于支撑中部,边界约束条件应等效为一个铰和一段弹簧[图21(b)],有效长度系数K′取2.0时[图21(c)]的屈曲荷载计算值与试验值吻合良好。对于普通钢支撑框架[40],有效长度系数K′可取0.65[图21(d)]。
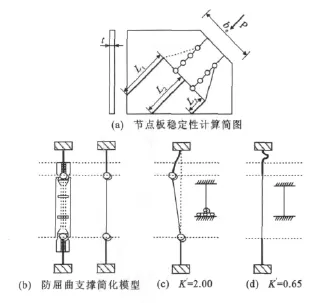
图21 防屈曲支撑框架节点板的稳定性Fig.21 Stability of Gusset Plate in BRB Frame
Fahnestock等[41-42]对4层钢管混凝土约束防屈曲支撑框架进行了足尺寸试验,框架与防屈曲支撑采用铰接节点连接(图22)。试验结果表明,梁梁拼接节点无论采用螺栓拼接还是连续焊接,防屈曲支撑框架均表现出良好的性能,层间位移角可在0.03以上,梁翼缘发生屈服之前节点区未出现明显的面外变形。该节点的良好性能来源于以下2个方面:①防屈曲支撑端部销轴尽量靠近梁柱节点,从而减小了节点板尺寸,提高了宽厚比,试验节点板的自由边宽厚比为7~10;②防屈曲支撑端部设置套管,限制了内核外伸段的面外变形。

图22 防屈曲支撑框架的铰接节点Fig.22 Hinged Node of BRB Frame
虽然铰接节点使防屈曲支撑的受力状态更接近理想轴压状态,但目前刚接节点的应用范围更广。因为相比于铰接边界条件,刚接边界约束能有效防止内核外伸段发生过大的侧向变形而导致的破坏,两端刚接防屈曲支撑表现出更佳的受力性能,即使是在实际框架结构中支撑两端出现转角变形时亦然。另外,铰接节点销轴连接施工时的间隙难以消除,防屈曲支撑承受反复拉压作用时不可避免地出现空程滑动。
针对防屈曲框架试验中容易出现的节点板面外屈曲以及反复荷载作用下节点板周围焊缝撕裂等问题,Berman等对防屈曲支撑框架的一种改进节点进行了试验研究。这种节点的改进之处在于,节点板仅与梁相连而不与柱子相连(图23),梁柱刚接连接,这种构造还可以减少框架传递给防屈曲支撑的面内弯矩。试验结果表明,当层间位移角达到0.03时,节点未发生破坏,该新型节点可替代传统节点用于加固改造工程。

图23 防屈曲支撑框架的一种改进节点Fig.23 An Improved Node of BRB Frame
文献[23]中进行了V形防屈曲支撑框架的疲劳试验,框架中采用双钢板双钢管的防屈曲支撑。试验结果表明,将螺栓容许应力提高至1.7倍的设计方法合理可靠,连接部分不发生滑动。
5 结语
(1)与传统整体式防屈曲支撑类似,一字形内核装配式防屈曲支撑中内核对外围约束构件的侧向挤压力由内核整体单波弯曲变形和整体多波变形引起;对于十字形内核的防屈曲支撑,内核高阶扭转变形也会使外围约束构件受到侧向挤压力,通过限制内核板件宽厚比可避免截面扭转变形发生。由于外围约束构件仅靠有限个螺栓连接,内核与外围约束构件的挤压作用更为复杂,且外围构件约束刚度应在同类整体式约束刚度的基础上进行折减。
(2)螺栓应具有足够的强度和合理的间距,保证外围约束构件作为整体工作,为内核提供有效约束,同时避免单个约束单元在螺栓间的自由段发生局部弯曲破坏。
(3)在防屈曲支撑框架中,支撑两端的转动使防屈曲支撑承受附加弯矩,在设计中应考虑这一不利影响。此外,防屈曲支撑与框架连接节点构造也是设计的重点,应保证内核外伸段以及支撑与框架连接的节点板具有足够的承载能力。
[1]TSAI K C,LIN S L.Study of All Metal and Detachable Buckling Restrained Braces[R].Taipei:National Taiwan University,2003.
[2]TREMBLAY R,BOLDUC P,NEVILLE R,et al.Seismic Testing and Performance of Buckling-restrained Bracing Systems[J].Canadian Journal of Civil Engineering,2006,33(2):183-198.
[3]USAMI T,GE H B,KASAI A.Overall Buckling Prevention Condition of Buckling Restrained Braces as a Structural Control Damper[C]//WCEE.Proceedings of the 14th World Conference on Earthquake Engineering.Beijing:WCEE,2008:1-8.
[4]郭彦林,江磊鑫.型钢组合装配式防屈曲支撑性能及设计方法研究[J].建筑结构,2010,40(1):30-37.
GUO Yan-lin,JIANG Lei-xin.Behavior and Application of Buckling-restrained Braces Assembled with Section Steels[J].Building Structure,2010,40(1):30-37.
[5]郭彦林,江磊鑫.双矩管带肋约束型装配式防屈曲支撑的设计方法[J].建筑科学与工程学报,2010,27(2):67-74,82.
GUO Yan-lin,JIANG Lei-xin.Design Method of Buckling-restrained Braces Assembled with Dual Ribbed Rectangular Hollow[J].Journal of Architecture and Civil Engineering,2010,27(2):67-74,82.
[6]CHOU C C,CHEN S Y.Subassemblage Tests and Finite Element Analyses of Sandwiched Buckling Restrained Braces[J].Engineering Structures,2010,32(8):2108-2121.
[7]GENNA F,GELFI P.Analysis of the Lateral Thrust in Bolted Steel Buckling-restrained BracesⅠ:Experimental and Numerical Results[J].Journal of Structural Engineering,2012,138(10):1231-1243.
[8]GENNA F,GELFI P.Analysis of the Lateral Thrust in Bolted Steel Buckling-restrained Braces Ⅱ:Engineering Analytical Estimates[J].Journal of Structural Engineering,2012,138(10):1244-1254.
[9]USAMI T,WANG C L,FUNAYAMA J.Developing High-performance Aluminum Alloy Buckling Restrained Braces Based on Series of Low-cycle Fatigue Tests[J].Earthquake Engineering & Structural Dynamics,2012,41(4):643-661.
[10]江磊鑫.装配式防屈曲耗能支撑构件设计方法研究[D].北京:清华大学,2010.
JIANG Lei-xin.Research on the Design Methods of Assembled Buckling-restrained Braces[D].Beijing:Tsinghua University,2010.
[11]WANG X,GUO Y,TIAN G,et al.A Design Method for a New Type of Assembled Steel Buckling-restrained Braces[C]//CHAN S L,SHU G P.Proceeding of Seventh International Conference on Advances in Steel Structures.Nanjing:Southeast University Press,2012:1042-1051.
[12]GB 50017—2003,钢结构设计规范[S].GB 50017—2003,Code for Design of Steel Structures[S].
[13]韩林海,杨有福.现代钢管混凝土结构技术[M].北京:中国建筑工业出版社,2007.
HAN Lin-hai,YANG You-fu.Modern Structure Technique of Concrete-filled Steel Tube[M].Beijing:China Architecture &Building Press,2007.
[14]AIJ 1997,Recommendations for Design and Construction of Concrete Filled Steel Tubular Structures[S].
[15]BS 5400:2005,Steel,Concrete and Composite Bridges,Part 5:Code of Practice for Design of Composite Bridges[S].
[16]ENV 1994 1-1:2004,Eurocode 4:Design of Composite Steel and Concrete Structures.Part 1.1:General Rules and Rules for Buildings[S].
[17]AISC LRFD:2005,Load and Resistance Factor Design Specification for Structural Steel Building[S].
[18]DBJ 13-51—2003,钢管混凝土结构技术规程[S].DBJ 13-51—2003,Technical Specification for Concrete-filled Steel Tubular Structures[S].
[19]郭彦林,王小安.一种四角钢组合约束型防屈曲支撑的外围约束机理及刚度取值研究[J].土木工程学报,2012,45(11):79-87.
GUO Yan-lin,WANG Xiao-an.Study on Restraint Stiffness of a Four-angle Assembled Steel Bucklingrestrained Brace[J].China Civil Engineering Journal,2012,45(11):79-87.
[20]TAKAHASHI S,MOCHIZUKI N.Experimental Study on Buckling of Unbonded Braces Under Axial Compressive Force:Part 1[C]//AIJ.Summaries of Technical Papers of Annual Meeting 1997.Tokyo:AIJ,1979:1623-1626.
[21]FUJIMOTO M,WADA A,SAEKI E.A Study on the Unbonded Brace Encased in Buckling-restraining Concrete and Steel Tube[J].Journal of Structural and Construction Engineering,1988,34B:249-258.
[22]郭彦林,王小安,江磊鑫.装配式防屈曲支撑构件及框架设计理论[J].结构工程师,2010,26(6):164-176.
GUO Yan-lin,WANG Xiao-an,JIANG Lei-xin.Design Theory of Assembled Buckling-restrained Braces and Buckling-restrained Braced Frames[J].Structural Engineers,2010,26(6):164-176.
[23]蔡克铨,黄彦智,翁崇兴.双管式挫屈束制(屈曲约束)支撑之耐震行为与应用[J].建筑钢结构进展,2005,7(3):1-8.
TSAI Keh-chyuan,HWANG Yean-chih,WENG Chung-shing.Seismic Performance and Applications of Double-tube Buckling-restrained Braces[J].Progress in Steel Building Structures,2005,7(3):1-8.
[24]陈正诚.钢侧撑韧性斜撑构材之行为与应用(Ⅰ)[J].建筑钢结构进展,2005,7(5):26-32.
CHEN Cheng-cheng.Behavior and Application of Buckling Inhibited Braces with Steel Lateral Support Elements(Ⅰ)[J].Progress in Steel Building Structures,2005,7(5):26-32.
[25]AISC 341-05,Seismic Provisions for Structural Steel Buildings[S].
[26]FEMA 450,Recommended Provisions for Seismic Regulations for New Buildings and Other Structures[S].
[27]IWATA M,MURAI M.Buckling-restrained Brace Using Steel Mortar Planks:Performance Evaluation as a Hysteretic Damper[J].Earthquake Engineering& Structural Dynamics,2006,35(14):1807-1826.
[28]NARIHARA H,TSUJITA O,KOETEKA Y.The Experimental Study on Buckling Restrained Braces:Part 1[C]//AIJ.Summaries of Technical Papers of Annual Meeting 2000.Tokyo:AIJ,2000:911-914.
[29]JU Y K,KIM M H,KIM J,et al.Component Tests of Buckling-restrained Braces with Unconstrained Length[J].Engineering Structures,2009,31(2):507-516.
[30]赵俊贤,吴 斌,欧进萍.新型全钢防屈曲支撑的拟静力滞回性能试验[J].土木工程学报,2011,44(4):60-70.
ZHAO Jun-xian,WU Bin,OU Jin-ping.Uniaxial Quasi-static Cyclic Tests on the Hysteretic Behavior of a Novel Type of All-steel Buckling-restrained Brace[J].China Civil Engineering Journal,2011,44(4):60-70.
[31]TIMOSHENKO S P,GERE J M.Theory of Elastic Stability[M].New York:McGraw-Hill,1961.
[32]STOWELL E Z.Unified Theory of Plastic Buckling of Columns and Plates[R].Kitty Hawk:National Advisory Committee for Aeronautics,1948.
[33]BLEICH F.Buckling Strength of Metal Structures[M].New York:McGraw-Hill,1952.
[34]MAKRIS N.Plastic Torsional Buckling of Cruciform Compression Members[J].Journal of Engineering Mechanics,2003,129(6):689-696.
[35]BLACK C J,MAKRIS N,AIKEN L D.Component Testing,Seismic Evaluation and Characterization of Buckling-restrained Braces[J].Journal of Structural Engineering,2004,130(6):880-894.
[36]TSAI K C,HSIAO P C,WANG K J,et al.Pseudo-Dynamic Tests of a Full-scale CFT/BRB Frame—PartⅠ:Specimen Design,Experiment and Analysis[J].Earthquake Engineering & Structural Dynamics,2008,37(7):1081-1098.
[37]TSAI K C,HSIAO P C.Pseudo-dynamic Tests of a Full-scale CFT/BRB Frame—Part Ⅱ:Seismic Performance of Buckling-restrained Braces and Connections[J].Earthquake Engineering & Structural Dynamics,2008,37(7):1099-1115.
[38]USAMI T,KANEKO H.Strength of H-shaped Brace Constrained Flexural Buckling Having Unconstrained Area at Both Ends—Both Ends Simply Supported[J].Journal of Structural and Construction Engineering,2001(542):171-177.
[39]ZHAO J X,WU B,OU J P.A Novel Type of Angle Steel Buckling-restrained Brace:Cyclic Behavior and Failure Mechanism[J].Earthquake Engineering &Structural Dynamics,2011,40(10):1083-1102.
[40]THORNTON W A.Bracing Connections for Heavy Construction[J].AISC Engineering Journal,1984,21(3):139-148.
[41]FAHNESTOCK L A,RICHARD S,RICLES J M.Seismic Response and Performance of Buckling-restrained Braced Frames[J].Journal of Structural Engineering,2007,133(9):1195-1204.
[42]FAHNESTOCK L A,RICLES J M,RICHARD S.Experimental Evaluation of a Large-scale Buckling-restrained Braced Frame[J].Journal of Structural Engineering,2007,133(9):1205-1214.

