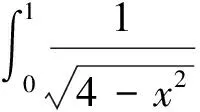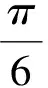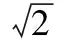一个椭圆积分的解与估值

肖业胜

(武汉工程职业技术学院，湖北 武汉 430080)

一个椭圆积分的解与估值

肖业胜

(武汉工程职业技术学院，湖北 武汉 430080)

椭圆积分；幂级数；Mathematica

在积分学中，椭圆积分最初出现于椭圆的弧长有关的问题中.Guilio Fagnano和欧拉是最早的研究者.通常，每个椭圆积分可以变为只涉及有理函数和三个经典形式的积分，即，第一，第二和第三类的椭圆积分.但是，椭圆积分不能用基本函数来表达.本文仅讨论一个具体的椭圆积分：

(1)

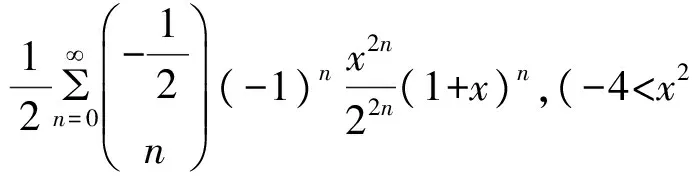
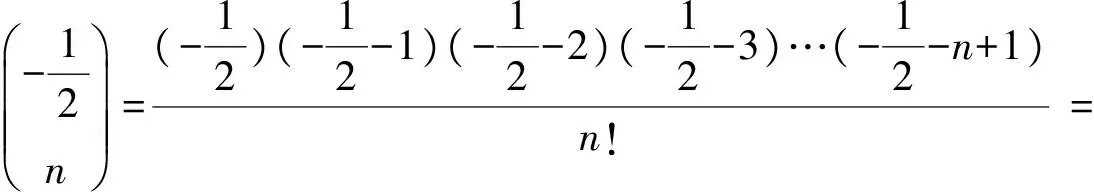
(注意：x∈[-1.1]⊂{x|-4

这样，求得了式(1)的值，其结果是一个无穷和，可以用其部分和来近似地表示积分的值.下面估计式(1)的值.当04-x2-x3>4-2x2，

只当x=0时，联立不等式左边取等号，当x=0或x=1时，联立不等式左边取等号.所以，

(2)

最后，借助数学软件Mathematica[1-2]求出式(1)的近似值，并式(2)的正确性.

首先，方程4-x2-x3=0的全部解为：

In[1]= NSolve[4-x^2-x^3□0,x]

Out[1]= {{x→-1.1573-1.30515TM},{x→-1.1573+1.30515TM},{x→1.3146}}

可以看出，在平面上，以坐标原点为中心的单位圆内，式(1)的被积函数无间断点.

由软件计算，式(1)的数值积分值为：

In[2]=NIntegrate[1/Sqrt[4-x^2-x^3],{x,0,1}]

Out[2]=0.547962

In[3]=Integrate[1/Sqrt[4-x^2],{x,0,1}]

Out[3]=π/6

In[4]=NIntegrate[1/Sqrt[4-x^2],{x,0,1}]

Out[4]=0.523599

In[5]=Integrate[1/Sqrt[4-2x^2],{x,0,1}]

In[6]=NIntegrate[1/Sqrt[4-2x^2],{x,0,1}]

Out[6]=0.55536

这就验证了式(2)是成立的.

本文讨论了椭圆积分式(1)的幂级数解法及积分的估值问题，借助计算机软件计算，给出了式(1)的近似值，并验证了估计式(2)的正确性.

[1] 同济大学数学系.高等数学[M].北京:高等教育出版社，2007.

[2] 李亚杰,黄根隆.数学实验[M].北京:高等教育出版社，2004.

SolutionandEstimationofAnEllipticIntegral

XIAO Ye-sheng

(Wuhan Engineering Institute,Wuhan 430080,China)

elliptic integral;power series;Mathematica

2013-03-24.

肖业胜(1956- )，男，副教授，主要从事基础数学的研究.

O172.1

A

1008-8423(2013)02-0194-02