两种编制地位指数表方法的比较

邹云波，朱于勤，冯 骏

(1.建始县国有东坪林场,湖北 建始 445300; 2.建始县国有长岭岗林场,湖北 建始 445300)

两种编制地位指数表方法的比较

邹云波1，朱于勤2，冯 骏2

(1.建始县国有东坪林场,湖北 建始 445300; 2.建始县国有长岭岗林场,湖北 建始 445300)

以马尾松优势木的解析木为基础，得出导向曲线.并分别利用标准差调整法和比例法即相对优势高法编制地位指数表.利用直观比较、采用卡方检验、剩余标准差、剩余残差平方和计算指标对比两种编表方法的精度.最终确定利用比例法编制的马尾松地位指数表更适宜于在福建地区使用的结论.

标准差调整;比例法;精度;地位指数表

地位指数表是林木立地质量评价的重要参考依据.森林立地分类及立地质量评价是达到科学造林、育林的十分重要的基础工作[1].目前常用的地位指数表编制方法主要有：标准差调整法、变动系数调整法、比例法(又称相对优势高法)、差分方程法.目前应用最广泛的编制方法主要是标准差调整法以及比例法.由于不同的编制方法所获得的地位指数表精度不同、准确率不同，因此选择有效的地位指数表编制方法对于森林立地质量评价、收获量预测就十分重要.本文选择标准差调整法和比例法这两种方法进行对比研究.

1 资料来源及导向曲线的确定

根据福建省青山纸业股份有限公司在福建省的三明与南平地区的各县收集98株马尾松优势木的解析木材料为资料[2]，整理数据采用最小二乘法或非线性拟合技术，拟合树高生长曲线.树高生长曲线是生物生长方程中的一种.它的总平均生长曲线，即树高生长随机过程的期望函数，在地位指数表中称为导向曲线.它的图形近似呈单调递增型的S形曲线[3].经过对比采用Korf方程[4].H=ae-bt-c作为优势木高生长模型精度最高.

经拟合得到的导向曲线为：

H=50.8221exp(-7.6269A-0.5996)

(1)

检验R2=0.987，方程较为准确.

2 基准年龄及指数级距的确定

2.1 基准年龄的确定

在导向曲线已确定的基础上，以基准年龄为导向曲线值为准，按指数级距展开得到各级地位指数曲线.得到15 a树高相对变动较大，到20 a左右树高生长趋于稳定.又因郎建奎教授[5]于1999年撰文中国主要树种的标准年龄为20 a，因此将树高标准年龄定为20 a，即A0=20.

2.2 地位指数级距的确定

根据马尾松的经营水平和生长特性，以2 m作为本次编表的级距，分成8、10、12、14、16、18、20等7个指数级.

求算各指数级各龄阶的平均优势高, 以此作为模型研制的基础数据.

3 编制地位指数表

3.1 利用标准差调整法编制地位指数表

3.1.1 拟合各树高标准差方程 以导向曲线为基础，按标准年龄时的树高值和指数级距，调整标准差，即可得到地位指数表及地位指数曲线簇.核算出各龄阶树高标准差，利用:

SH=a+blg(A)

(2)

式拟合龄阶树高标注差方程.本方程为：

SH=5.6268exp(-5.7663A-0.9195)

(3)

将各龄阶代入式(2)，即可计算出龄阶树高标准差理论值SAi.

3.1.2 导算地位指数表 在基准年龄A0=20时，导向曲线的理论树高值为H0=14.3，而相近的地位指数级为S0=14，则应进行调整(即将14.3 m降为14 m),根据H0与S0的大小，可用下式进行调整：

(4)

式中:Hij—第i龄阶第j指数级调整后的树高；Hik—第i龄阶导向曲线的树高；H0j—基准年龄时第j指数级的树高；H0k—基准年龄时导向曲线的树高；SA0—基准年龄所在龄阶树高标准差理论值；SAi—第i龄阶树高标准差理论值.

标准差调整法所用调整系数为：

(5)

则可推算出个龄阶的树高调整值及14指数级为基础各龄阶调整后的树高值.

以调整后的导向曲线为准，按照指数级距C=2 m，逐龄推算各地位指数级曲线上的树高值，其余指数级的调整系数Kj为：

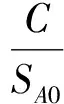
(6)

由式(6)可推导出Kj=0.513，按照式(4)可推导计算各龄阶内各地位指数级的树高值.

根据表各龄阶内各地位指数级的树高值的内容，根据相邻指数级：

(7)

可以列示出地位指数表(表1).

3.2 利用比例法编制地位指数表

比例法即相对优势高法，是按照一定比例将导向曲线平移的一种方法[6]，在拟合导向曲线方程后，将各龄阶值代入该方程，以各地位指数级与基准年龄理论树高之比作为调整比例系数，即可推导出地位指数表及地位指数曲线簇.

3.2.1 导算各地位指数级调整系数 以导向曲线为基础，将各龄阶代入式(1)，即可求出各龄阶理论树高值Hik,其基准年龄A=20时H0k=14.3 m，其地位指数级为14，根据其指数级距，分出8个地位指数级.各指数级系数根据公式：

(8)

式中αj表示第j指数级调整系数；Hd表示地位指数；H0k表示基准年龄的理论树高值.

表1 用标准差调整法编制的福建马尾松地位指数表(A0=20 a，C=2)

3.2.2 导算地位指数表 以2 m为指数级距，将地位指数分别代入：

Hij=αj×Hik

(9)

即可得到各龄阶时各地位指数级的优势高.

根据式9、7,可以列示出地位指数表(见表2).

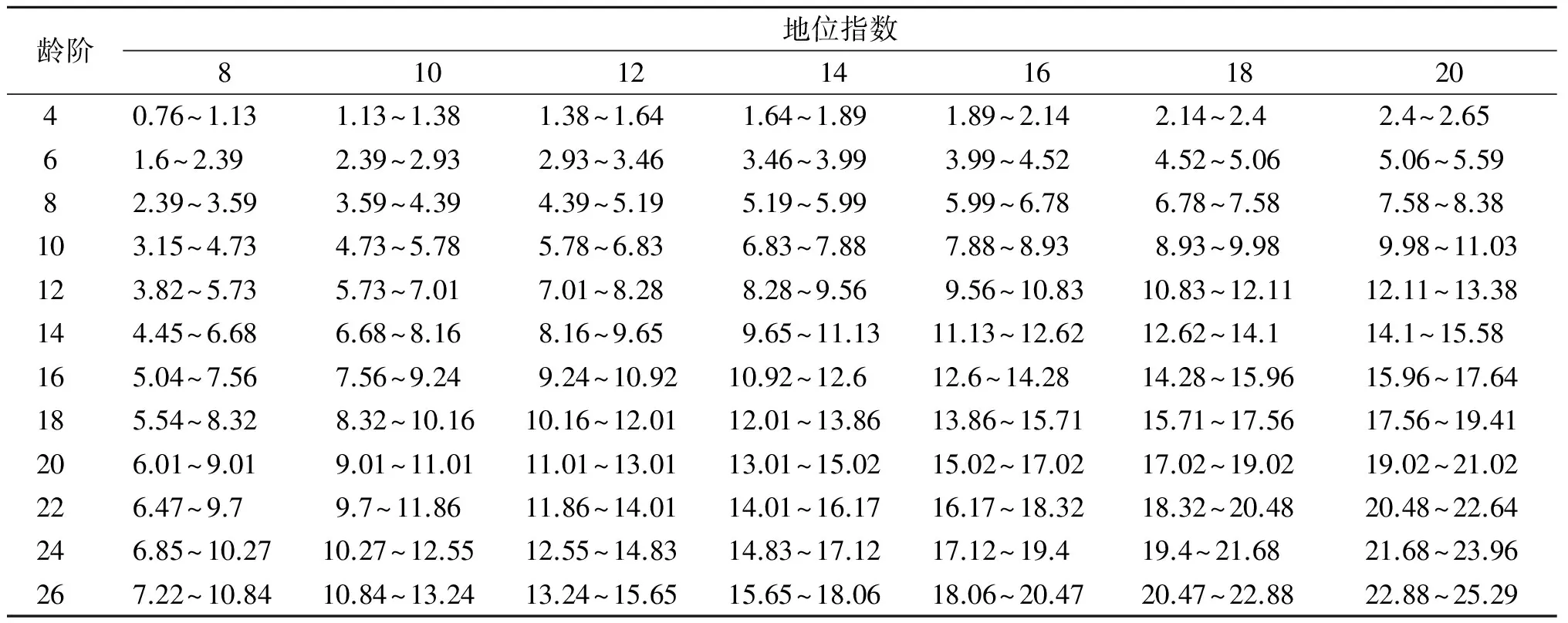
表2 用比例法编制的福建杉木地位指数表(A0=20 a，C=2)

4 对比分析

4.1 直观比较

依据表1和表2分别绘制出出两种地位指数表不同指数级树木优势高随年龄变化的曲线，即地位指数曲线簇，见图1、2.

图1 用标准差调整法编制的地位指数曲线 图2 用比例法编制的地位指数曲线

由图1、2可看出，两种方法所编制的地位指数表与导向曲线基本一致，图中14指数级的曲线即为导向曲线.各指数级曲线分布在14指数级两侧，并且依指数大小分布.直观上，两种方法所编制的地位指数表都符合导向曲线.

4.2 精度比较

4.2.1 卡方检验比较 计算统计量K2

(10)

式中：A代表实际经解析所得到的地位指数；T代表理论的地位指数，即以编制出的地位指数表查询得到的地位指数.

式(10)经推导可得下式:

(11)

(12)

依照式(11)进行计算.得出两种编制方法检测的K2值.

经计算可知比例法的卡方检验变量的综合值为10.37,而利用标准差调整法所得卡方综合值为4.96.可见利用比例法编制的地位指数表的相关性更强，对于地位指数和树高的预测更为准确.

4.2.2 剩余残差平方和比较 为分析两种方法所产生的随机误差大小，选用各龄阶各指数级样本与两种方法的理论值进行比较，计算出各自的剩余残差平方和.可采用式(13)进行计算.

(13)

式中：Q为剩余残差平方和；his为样本实际树高；hij为理论树高.

按照式(13)，将解析木实际树高与理论树高值进行计算.计算采用标准差调整法和比例法编制的地位指数表的剩余残差平方和结果.各指数级残差平方和经计算对比如表3.

表3 两种编表方法的残差平方和对比Tab.3 Two kinds of compilation methods and comparative residual sum of squares

从表3可以看出，利用标准差调整法和比例法两种方法分别编制地位指数表最终的总体残差平方和区别不大，标准差调整法总体残差平方和略高于比例法，但在不同地位指数级两种方法各自的残差平方和各有高低.因此在不同地位指数级两者的精度高低是不同的.

4.2.3 剩余标准差比较 由于通过剩余残差平方和计算的结果可比性不强，为了进一步验证两种方法的回归精度，采用剩余标准差进行比较，依式(14)进行计算：

(14)

式中：S代表剩余标准差；his为样本实际树高；hij为理论树高；n代表所取样本数.分别计算各地位指数级的剩余标准差，得到结果如表4.根据表4，利用标准差调整法编制的地位指数表和利用比例法编制的地位指数表依然表现为在不同指数级其剩余标准差高低不同.总体上利用比例法编制的地位指数表的剩余标准差较利用标准差调整法编制的地位指数表的剩余标准差略低.因此，总体上，利用比例法编制的地位指数表精度较高.

表4 利用标准差调整法和比例法编制地位指数表的剩余标准差对比

5 结论

通过各种检验，发现利用比例法编制的福建马尾松地位指数表较利用标准差调整法编制的福建马尾松地位指数表的精度更高，适用性更强.分析产生这种结果的原因主要有以下几个方面：

1)马尾松的采伐年龄定在20龄，比例法由于采用的是按一定比例将导向曲线平移的方法编制的，因而在低龄阶的林木中线性相关性更强而显著.而一旦在较高龄阶中使用时也容易产生偏差.

2)本次编表使用的是同一导向曲线，而且仅仅是依靠福建个别地区的马尾松解析木数据，因而也与当地的各种其他气候与环境条件产生了一些影响，原始数据的处理可能带来一些误差.

可以确定，利用比例法(即相对优势高法)编制的地位指数表在对于福建地区的马尾松低龄人工林的参考意义较强.

[1] 张咏祀.标准差法在森林立地质量评价中的应用[J].西华师范大学学报,2008,29(4):48-351.

[2] 陈杜满.马尾松造纸原料林地位指数曲线模型[J].福建林学院学报，2002,22(2):164-168.

[3] 孟宪宇.测树学[M].北京：中国林业出版社，1995.

[4] 李凤日,伊尹, 刘刚.广义korf方程的推导及其应用[J].林业资源管理，1997(特)：212-216.

[5] 朗奎键，张富，胡光，等.中国主要树种标准化地位指数函数的研究[J].东北林业大学学报，1999，27(2)：1-5.

[6] 朱晓青.塞罕坝华北落叶松人工林地位指数表的研制[J].山东林业科技,2010,40(6):34-35.

ComparisonofTwoMethodsPreparingSiteIndexTable

ZOU Yun-bo1,ZHU Yu-Qin2,FENG Chun2

(1.Jianshi Dongping Forest Farm,Jianshi 445300,China;2.Jianshi Changlinggang Forest Farm,Jianshi 445300,China)

Based on the analytic trees of dominant Masson pine trees,the guide curve was obtained.The standard deviation method were used to prepare the site index tables.The intuitive comparison,the chi-square test, residual standard deviation, and the remaining sum of squared residuals were used to compare the accuracy of the two methods.The result is that the site index table with the ratio method is more suitable for use in Fujian area.

method of standard deviation adjustment;ratio method; accuracy;index table

2013-04-16.

邹云波(1977- ),男(土家族)，助理工程师，主要从事森林经营管理的研究.

S759.8

A

1008-8423(2013)02-0158-05