中压配电网载波通信调制解调技术研究*
谢志远,杨 星,贡振岗,吴晓燕,郭以贺
(华北电力大学 电气与电子工程学院,河北 保定 071003)
中压配电网载波通信是指利用10 kV配电网现有的物理网络进行数据通信和信息传递的技术。配电网在我国的建设已经相当完善,利用配电网实现通信,不需要重新布线,成本低廉,因此受到人们的广泛关注。同时,电力线信道噪声干扰强、频率选择性衰落复杂的传输特性,严重制约着电力线通信的发展。而调制方式的加入是有效解决这一问题的关键技术之一。早期的窄带调制方式技术简单、容易实现,但随着数据传输速率的提高,传统的窄带通信已经不能满足要求,新的调制技术——正交频分复用OFDM(Orthogonal Frequency Division Multiplex)在抗干扰、抗多径特性以及抗衰减方面具有很强的能力,尤其适用于电力线高速数字通信,因此成为目前配电网载波通信调制方式中的研究热点。
本文首先介绍了OFDM的调制原理,针对中压电力线信道的特点,基于传输线理论建立了其衰减特性模型,仿真了此信道情况下OFDM的误码率性能,以及信道特性逐渐恶劣的情况下[1],OFDM的抗频率选择性衰落能力,为更好地发挥OFDM在中压配电网载波通信中的优势提供一定的参考。
1 正交频分复用原理
正交频分复用是一种特殊的多载波调制技术[2-3],通过将发送的数据流分解为多个子比特流,使每个子数据流的速率迅速降低,从而大大提高了其抗信道衰落、抗多径的能力。将原信号序列分割成N个子信号后,子信号的码元速率降为原来的1/N倍,即Rb/N,周期为Ts=NT。然后用这N个子信号分别去调制N个相互正交的子载波,各个子信道的已调制信号相加就形成了OFDM发射信号。实际输出的信号可以表示为:

式中dn(t)为第n个子载波上的复数信号。dn(t)在一个符号期间Ts上为常数,即dn(t)=dn。OFDM信号又可以用复数形式表示为:

其中,ωn=ωc+n△ω为第n个子载波角频率,基带处理时可令ωc=0,因为OFDM信号首先经过基带调制,然后经过上变频送入信道。对式(2)进行简化后以采样间隔T采样,则有:

而离散傅里叶变换(IDFT)形式为:
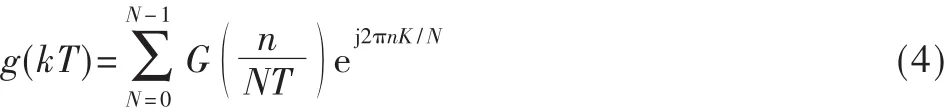
由图1可见,OFDM在信号发送时,先对伯努利二进制信号发生器产生的44 bit(一帧)源数据进行RS(15,11)编码,再进行QPSK信道映射得到30 bit有效数据,根据快速傅里叶逆变换(IFFT)定义,要把数据插在低频处,需要将所得30 bit数据搬移到IFFT的两边,中间补零,第一位0为DC子载波,接收时容易受到干扰所以也插零。因此有效数据所在位置为[2:16,50:64],其余位为0。再经过快速傅里叶逆变换(IFFT)将频域信号转变为时域信号,IFFT长度为 64,Selector模块参数设置为[39:64,1:64]将后26个数据搬移到数据前端作循环前缀,并进行并/串变换后送入信道。该信道为电力线信道模型,噪声假设为高斯白噪声。接收端除了加入信道估计和信道补偿部分外,与发送端过程相反。
2 中压电力线信道模型
对中压电力线信道进行建模,主要考虑强烈的噪声干扰和复杂的衰减特性对信号的影响。本文假设噪声为高斯白噪声,重点对信道的衰减特性进行分析,利用传输线理论建立其模型。
2.1 均匀双导体传输线理论[4]
2.1.1 均匀架空线
随着配电网载波通信技术的发展,对传输线的研究越来越深入。一段架空电缆若各处有相同的尺寸、相同的材质,即为典型的均匀传输线,可以用二端口网络模型表示,如图2所示。设:


图2 二端口网络模型
其中网络的转移参数矩阵为:
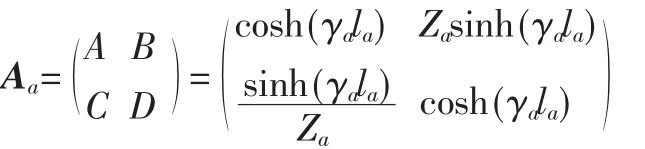
la表示线缆长度,γa表示线缆的传播常数,Zz则为线缆的特性阻抗。
2.1.2 分支线路
网络中经常存在分支线路,其影响可以归结为等效输入阻抗并联在主干线上,输入阻抗的传输参数矩阵为:

输入阻抗为:

其中la为分支线的长度,Zb为特性阻抗,γa为传播常数,Zlb为终端所接变压器的等效阻抗。
2.1.3 总体模型
电力线信道由不同架空线的串联单元和不同分支线的并联单元组成。由以上分析可知,要建立电力线信道的模型,只需要把参数相同的一段主干线路或分支线的输入阻抗等效成一个二端口网络,再将其级联即可。

若每一个二端网络的转移矩阵为Ai,则级联后总的矩阵为:

2.2 均匀多导体传输线理论
配电网络并不能直接用平行双线系统描述,而是需要用多导体传输线理论,因为电力系统中的输电线路多为交流三相或者直流双极模式,各导线间存在着相互耦合效应,利用模式变换可以消除其影响,且解耦后的各模分量仍然遵循传输线方程。多导体传输线电压、电流满足的是矩阵方程,对n+1根导线系统,它们用n阶列矩阵表示。 线路的原参数 R0、L0、C0也变成了矩 阵 R0n×n、L0n×n、C0n×n。线路阻抗矩阵和导纳矩阵为 Z0=R0+jωL0,Y0=G0+jωC0。
将双导体传输线方程中的电流、电压、单位长度的电容、电感均用矩阵表示,即得:

传输线方程的解为:

式(10)中的四个链参数用双曲线正弦及双曲线余弦函数表示为:

其中Zc为特性阻抗,它是一个复数矩阵。
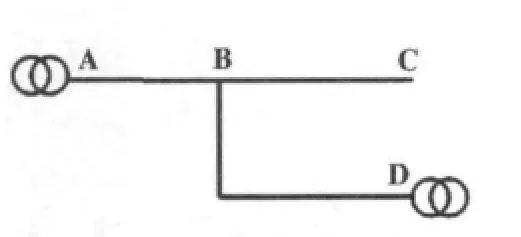
图3 配电网络的简化模型
基于以上传输线参数计算理论,根据实际的配电网络的结构,建立一个简单的仿真网络如图3所示,其中 AB段长度 150 m,BC段长度 100 m,BD段 30 m,A、D两侧为端接的配电变压器,A点为信号源所在位置。根据此仿真网络的拓扑结构,可以利用Simulink中三相输电线路模型进行建模,参数则可以由Power_lineparam工具计算得到,变压器采用参考文献[4]中的变压器简化模型。仿真得到了该信道衰减特性的计算结果,图4为仿真结果与实际测量的线路输入阻抗对比。从图中可以看出,随着频率的增加,信道呈现频率选择性衰减,这是因为电力线网络结构复杂,分支线路的存在以及元件参数的不同造成了阻抗不匹配以及信号的多径传播。严重时在某些频点上甚至出现深度衰落。

图4 10 kV线路衰减特性仿真与测量结果对比
3 仿真结果及分析
通过一系列的仿真测试,绘出了在所测量的信道特性下OFDM系统信噪比与误码率的关系曲线,如图5所示。可以看出,OFDM技术可以在电力线信道下实现可靠的数据传输,信噪比高于6 dB时,误码率明显下降;信噪比为13 dB时,误码率达到10-3以下;经 RS编码后信噪比在11.5 dB以上误码率即为零。可见编码方法的加入有效地提高了信号传输的可靠性。同时,由图4还可以看出,信噪比逐渐提高时,误码率下降却是比较缓慢的。这是因为系统中所有子载波的位置、调制方式等都是固定的,并没有因为信道特性的变化而进行动态调整,这样系统的误码率就取决于衰落最严重的子载波。
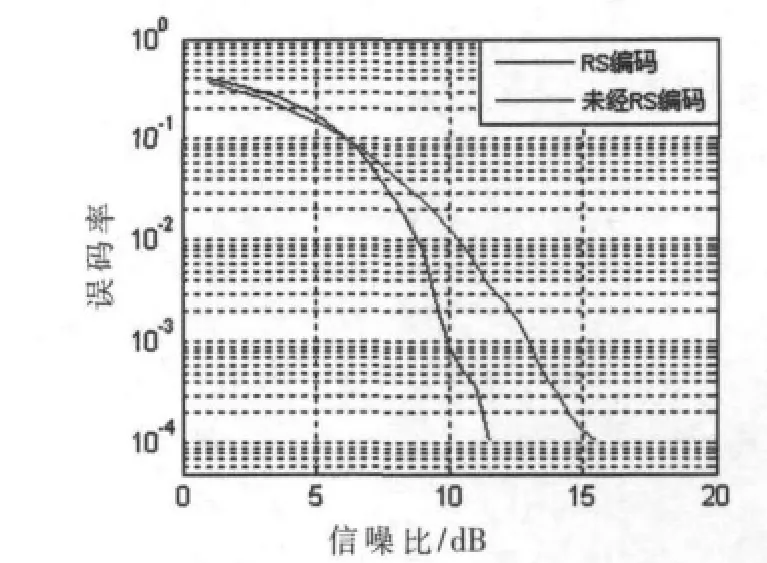
图5 电力线信道下系统误码率
随着电力线信道特性逐渐恶劣,深度衰减频段逐渐增加,信号传输的可靠性大受影响。图6画出了子载波通过率越来越大的情况下,信号的传输效果。未经RS编码时,当深度衰落高于12%,即子载波通过率低于88%时,误码率均在10-2以上,通信可视为中断;随着子载波不断增加误码率迅速下降,90%以后,误码率下降到10-4以下。经过RS编码,78%的子载波通过后误码率即为零,抗衰落性能得到明显改善。除了对信号进行编码以外,由于OFDM是把信道划分为若干子信道,可以根据信道实际传输情况灵活地分配发送功率和信息比特,更加有效地利用信道资源。

图6 恶劣信道下系统误码率
OFDM技术是现代电力线通信的关键技术,为研究其克服电力线信道频率选择性衰落的能力,本文在Matlab/Simulink平台上设计并实现了基于OFDM的中压电力线载波通信系统仿真,其中电力线信道是根据山西某中压配电网的衰减特性建模,仿真结果验证了OFDM技术在中压电力线多径衰落信道的条件下能够实现高速的数据通信。当信道特性逐渐恶劣时,深度衰落在12%以内的范围,OFDM仍能可靠通信,经过RS编码,78%的子载波通过后误码率即为零,明显地提高了系统抗多径衰落的能力。
[1]邢志民,侯思祖,李晶,等.中压电力线信道特性的测量与研究[J].华北电力技术,2005(10):1-4.
[2]樊昌信,曹丽娜.通信原理[M].北京:国防工业出版社,2009:251-256
[3]SOUISSI S,DHIA A B,TLILI F,et al.OFDM modem design and implementation for narrowband Power line communication[C].Design and Technology of Integrated Systems in Nanoscale Era(DTIS),May.2010:1-4.
[4]Guo Yihe,Xie Zhiyuan,Wang Yu.A model for 10kV overhead power line communication channel[C].International Symposium on Computer Science and Computational Technology(ISCSCT 2009),DEC 2009:289-292.
[5]孙立山,刘洪臣,王晓媛.传输线参数测试方法研究[J].电气电子教学学报,2008,30(5):18-23.
[6]CATALIOTTI A,CARA D D,FIORELLI R,et al.Powerline communication in medium-voltage system:simulation model and onfield experimental tests[J].Power Delivery,IEEE Transation on,2011,99:1.

