R－T－S平滑算法在POS数据后处理中的应用

郝万亮，孙付平

（信息工程大学 测绘学院，河南 郑州 450052）

近年来，POS系统发展迅速，其在军事侦察、航空摄影测量、移动测图等方面发挥着越来越重要的作用。作为一种高精度的定位定姿平台，POS充分利用DGPS/INS组合导航技术和一系列的后处理算法，来获取平台精确的位置和姿态信息。目前，工程上普遍采用卡尔曼滤波（kalman Filter，KF）对POS数据进行处理，但其精度有限，同时该方法在卫星信号失锁区间定位精度不高。加拿大的Applanix公司在其产品中成功应用了平滑技术，其具体细节未公开报道［1］。本文把反向R－T－S（Rauch－Tung－Streibel）平滑算法应用到POS数据后处理过程中，并对该算法进行了仿真分析，结果表明，该方法不仅能够大大减小定位定姿误差，而且在卫星信号失锁段精度也能大幅提高。

1 POS后处理算法

为了获取载体精确的位置及姿态信息，POS系统一般利用GPS差分技术来提高精度，例如伪距差分、载波相位差分等，然后再与惯导或里程仪组合，以及利用GPS双天线来抑制航向角的发散，进一步提高姿态精度。一方面GPS信息可以用来估计惯导设备的偏差；另一方面在卫星信号失锁时，惯导设备提供的信息可以用来估计载体的运动状态，从而减小卫星信号重新捕获所需的时间［2］。

平滑技术在POS数据后处理中起着重要的作用，理论上可以证明，经过平滑之后的精度比单向卡尔曼滤波精度更高［3］。POS后处理算法结构如图1所示。

图1 POS后处理算法结构

POS后处理算法主要包括两个过程：首先利用IMU测量的加速度、角速度进行惯性导航解算，将获得的位置、速度与经过差分处理的GPS信息同步做差，作为前向Kalman滤波的观测量。其次利用前向Kalman滤波过程中获得的协方差阵和状态转移矩阵，对状态估计值进行反向R－T－S平滑，根据平滑结果对惯性导航输出的位置、速度和姿态进行校正，作为POS的最终输出［4］。

2 平滑技术

平滑技术作为事后或准实时数据处理的一种方法，可以大大提高数据处理的精度，在测绘领域获得了广泛的应用。平滑技术分为3类：固定 区 间 平 滑（Fixed－Interval Smoothing）、固 定 点平滑（Fixed－Point Smoothing）和 固 定 滞 后 平 滑（Fixed－Lag Smoothing）［5－6］。其 中 固 定 区 间 平 滑在数据后处理中应用最为广泛，其示意图如图2所示。它是在前向卡尔曼滤波的基础上进行的反向滤波，充分利用了区间内所有时刻的测量值对状态进行估计，该方法能提供比单向滤波更高的精度，同时在卫星信号失锁段也是一种很好的桥接算法。

图2 固定区间平滑示意图

3 R－T－S平滑

R－T－S平滑是固定区间平滑的一种，它是Rauch等人于1965年提出的，该方法计算简单，工程实现容易，已被证明是一种有效的事后分析算法，可以获得比卡尔曼滤波精度更高的融合结果［7］。

R－T－S平滑由前向滤波和后向滤波组成，前向滤波是经典的卡尔曼滤波器，用来估计每一时刻的状态，后向滤波是在前向滤波的基础上获取更精确的状态估计值［2］。

对于式（1）的系统模型：

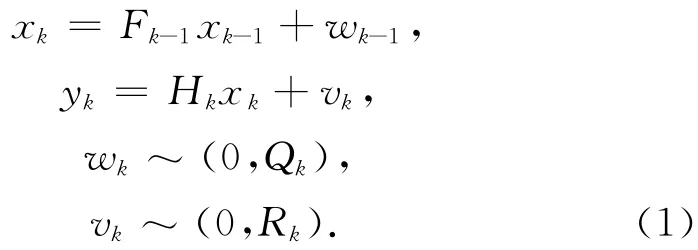
前向卡尔曼滤波估计的滤波初值

对于k＝1，2，…，m，执行下列卡尔曼滤波循环：

从而求得xm的前向估计值及其协方差。在前向卡尔曼滤波过程中存储实时状态估计值、状态预测值、误差估计协方差阵和预测误差估计协方差阵，以及系统的状态转移系数矩阵Fk－1。卡尔曼滤波完成后，利用存储的数据进行反向R－T－S平滑处理。

由式（3）可知，R－T－S平滑的公式是由k＝N－1到k＝0的递推过程，Kk为平滑增益，Pk为平滑误差估计协方差阵，是平滑滤波的状态变量［5］。通过R－T－S平滑处理，可以获得平滑区间内所有时刻的最佳估计值。

4 仿真及分析

为验证R－T－S平滑算法在POS数据后处理中的效果，进行了数值仿真，仿真条件设置如下：

1）设置仿真轨迹如图2所示，轨迹初始纬度φ＝39°，经度λ＝108°，高度h＝100m，初始速度0m/s，加速到100m/s后做匀速飞行。初始姿态角（0°，0°，0°）。惯导初始位置误差为（1m，1m，1m），速度误差（0.1m/s，0.1m/s，0.1m/s），姿态误差（100″，100″，300″）。

2）设陀螺仪常值漂移和随机漂移分别为0.1°/h和0.01°/h，加速度计常值零偏和随机零偏分别为100μg和10μg。

3）GPS速度误差不大于0.1m/s，位置误差不大于1m。

为验证该算法在卫星信号失锁区间的性能，在区间一（100～160s）、区间二（400～460s）和区间三（600～660s）内人为屏蔽掉卫星信号，如图3所示。

图3 仿真轨迹

位置和姿态的仿真结果如图4和图5所示。

图4 位置误差

图5 姿态误差

由图4和图5可以看出，在前向卡尔曼滤波的基础上进行反向R－T－S平滑，能够获得更高的位置和姿态精度，此效果在卫星信号失锁段尤其明显，在人为设置的3个卫星信号失锁区间的误差统计如表1所示。

表1 仿真误差统计

由表1中的统计数据可知，经过R－T－S平滑处理后的位置和姿态精度大大提高，在3个失锁区间内，位置误差由米级降为分米级甚至厘米级，精度能提高80%以上，姿态误差也能提高约60%，充分说明了该算法作为一种桥接算法的可行性。

5 结 论

为了获取高精度的定位定姿数据，将R－T－S平滑技术应用于POS数据后处理中，经过仿真分析表明，与传统的卡尔曼滤波方法相比，该方法不仅能够大大提高精度，而且在卫星信号失锁段也能取得理想的效果。该算法对于提高POS数据的精度，尤其是在卫星信号失锁的情况下的定位定姿能力，具有重要的意义。

［1］宫晓琳，房建成.基于SVD的R－T－S最优平滑在机载SAR运动补偿POS系统中的应用［J］.航空学报，2009，30（2）：311－312.

［2］SAMEH NASSAR.Different Algorithms for Bridging Kinematic DGPS Outages using SINS/DGPS Integration［C］//Proceeding of ION GPS2002.Portland，2002：1474－1482.

［3］SAMEH NASSAR.Improving the Inertial Navigation System（INS）Error Model for INS and INS/DGPS Applications［D］.Canada：University of Calgary，2003：100－106.

［4］邱宏波，周东灵，李文耀，等.基于闭环误差控制器的高精度POS后处理算法研究［J］.中国惯性技术学报，2010，18（6）：691－695.

［5］ARTHUR GELB.Appplied Optimal Estimation［M］.London：The M.I.T Press，1974：157－180.

［6］HANG LIU.Optimal Smoothing Techniques in Aided Inertial Navigation and SurveyingSystems［D］.Canada：University of Calgary，2009：55－70.

［7］李睿佳，李荣冰，刘建业，等.卫星/惯性组合导航高精度融合算法研究［J］.系统仿真学报，2010，22（1）：75－78.