GPS动态定位中的虚拟观测方程研究

崔建勇，陈明剑

（信息工程大学 测绘学院，河南 郑州 450052）

在高精度的GNSS定位应用中一般使用高精度的载波相位观测值。而使用载波相位观测值需要准确解算GNSS的整周模糊度［1－6］。而对于动态实时定位则需要单历元解算，但是单历元解算模糊度由于观测量较少而解算困难。目前常用方法之一是与其它导航系统，如GLONASS系统、INS系统等联合解算［7］。而这样又会增加整个系统的费用。第2种方法就是选用合理的函数解算模型。一旦选用的函数模型合理而有效，则求解载波相位的整周模糊度水到渠成［8］。在实际定位中，可根据载体运动的实际情况，尽量利用已有的信息，如载体已经解得的坐标、速度等信息，选取适当的函数模型，来进行整周模糊度的求解，卡尔曼滤波是最常用到的模型之一。卡尔曼滤波应用在GNSS动态定位的假设一般是载体的加速度为0或某一恒定值［5］，只有这样卡尔曼滤波才能具有较好的效果。而在实际GNSS动态定位中，这个条件往往不能满足，此时仍然只利用卡尔曼滤波的话，很难得到一个比较好的结果，而且极有可能使定位的结果扭曲［7，9］。所以要考虑一种新的模式来探讨动态情况下如何利用已有的解算结果来进行参数求解。

由于上述原因，由前一历元时刻k－1的载体状态量（包括坐标和速度）算出k历元的坐标，将其视作载体的一种虚拟观测量，再由它与双频码伪距和载波相位值进行单历元整周模糊度的解算。

1 常规模型

对GNSS短基线来说，双差可以有效消除测站及卫星星钟差、电离层延迟误差、星历误差等，其观测结果可表示为：

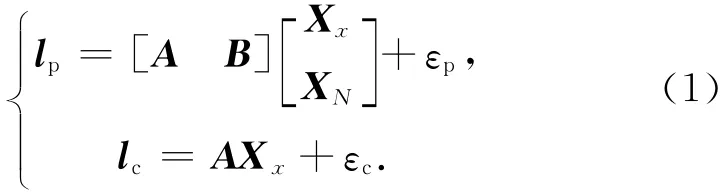
式中：lp为卫星双频相位观测量与计算值双差向量的差，lc为P码伪距观测量计算量的双差向量的差，A为n×3维基线坐标的改正量设计矩阵，B为n×m维模糊度向量设计矩阵，Xx，XN分别代表三维基线坐标改正量和m维待定的整周模糊度向量，εp为载波相位双差观测噪声，εc为伪距双差观测噪声。

在载波相位和码伪距联合进行参数解算时，由于它们的测量精度不同则解算中所赋的权也不相同。设pc为码伪距权，pp为载波相位的权，则一般取pc＝10－4pp。建立法方程

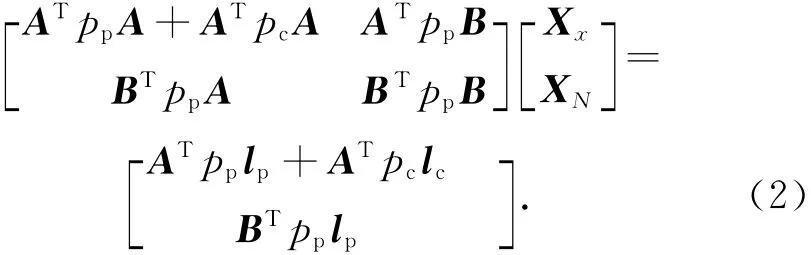
对于一直在运动的载体，利用最小二乘的结果即使在双频P码的情况下，也不是每历元都能确定整周模糊度。而利用卡尔曼滤波，当动态模型噪声在滤波中不能准确给定或任意历元的观测噪声不服从正态分布时，滤波结果的可靠性就会削弱［9］，此时卡尔曼滤波极可能致使滤波结果发散［5］。基于此，本文提出了根据第k－1和第k历元的信息建立虚拟观测方程的方法，使k时刻的定位结果得到有效利用且对后一历元时刻的解算结果不产生扭曲。

2 虚拟观测方程模型

2.1 定义

以已经解算得到的第k－1和第k历元的信息估算求得的k＋1历元基线分量作为虚拟观测值，它与准确解算出的结果差值作为噪声，虚拟观测方程可以表示为

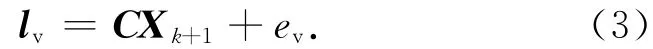
其中：

式中：lv为虚拟观测值，C为坐标分量的3×3设计阵，根据实际情况的不同，C也不同，为第k历元的参数解，ev为虚拟观测噪声，I3为三阶的单位阵，Δt表示k到k＋1历元的时间间隔，为第k历元的速度估值。

如果设pv为虚拟权（C的定义以及定权在下文详细论述），估计准则变为

式中：Vp为相位改正数，Vc为伪距改正数，Vv为虚拟观测值的改正数。在求偏导后可得法方程为

对法方程求逆得参数的浮动解。再利用LAMBDA方法固定载波相位模糊度后再代入法方程，得基线分量的固定解，形式如下：

式中：为模糊度的固定解，为基线分量改正数的固定解。

2.2 设计矩阵C和权pv的分析与确定

在形变监测中，基线坐标改正量均可以通过前一历元来推算，此时C为单位阵。但很多动态情况下，不是所有坐标改正量都是可以通过前一历元来推出求得，只能对能推算的坐标分量进行建立观测值。比如火车站大型货场或者港口的轨道起重机，一般是对Z方向推算，此时。在姿态测量中，由于基线长度固定［9］，C的取值可以表示为。r表示基线的长度，C的取值据载体运动状况而定。

虚拟观测值的权pv要能大体预测推算的k＋1历元的坐标值与k＋1历元真实的坐标值最大差，而后根据最大差与观测值所能达到的定位精度的比定权，比如，在形变观测中，在同一期观测中两个历元间发生的形变应该不会大于分米级，这与伪距差分的精度相当，因此，它可取相位权0.000 1。火车站或者货运码头的轨道吊塔沿固定轨道进行运动，速度比较慢，可以确定两历元间速度变化量级为分米每秒，因此，也可以通过此方法进行定权。

类比于卡尔曼滤波，当运动载体为匀速或匀加速时，pv可据解算的前一历元参数的方差阵和噪声的方差阵或先验信息来确定，此时等同于卡尔曼滤波。若pv取0，即为加权最小二乘法。约束条件也可以用虚拟观测方程的形式来表示，由于约束条件都与基线分量的坐标改正数有关，因此，都可以建立相应的虚拟观测方程，只不过C的取值不同而已，但此时pv要大于相位观测值的权。所以，pv的取值与解算结果直接相关。因此，pv的取值必须合理，一般有以下几个原则：①pv值不能过大，不能使k时刻的运动信息畸化或扭曲，否则会夸大虚拟值精度及其贡献并可能恶化结算结果。②pv的取值不能太小，否则对解算结果没有贡献，使得虚拟观测方程无存在的必要。

3 算 例

在某大学体育场进行实验，实验中使用两台接收机，参考站放置在体育场大约中心位置，流动站放在三轮车上绕跑道运动，实验时间为2011－03－13，采样间隔为1s，高度截止角15°。先让三轮车在跑道上静止1～2min，进行整周模糊度初始化。而后将车沿跑道运动，进行数据采集工作，共采集了1 000历元。

小车在跑道上运动时，在Z分量速度变化相对较小，因此，用k－1历元时刻推得k历元坐标精度相对于码伪距观测量的精度相当，因此，pv取载波相位权的1.0e－4。

一般来说，模糊度接受与否用Ratio检验。为了检验不同的虚拟观测权对ratio值的不同影响。将最小二乘的结果和取不同虚拟权ratio值之差进行了比较。结果如图1所示。

图1 不同约束条件下的ratio值增量比较

图1中分别取虚拟权为1.0e－3，1.0e－4，1.0e－5。从图1中可以看出，当加的权过大，图1（a）中的ratio值增量虽大部分历元增大，但是减小的历元也很多，说明虚拟观测值的取权过大，对解算结果有所扭曲。图1（b）中虽然极少数历元的ratio值增量减小，但是绝大部分历元的ratio值明显增加，图1（c）中基本没有历元的raito值减小，但是ratio值增量也不明显。因此，虚拟权取0.000 1较为适当。

不同虚拟权取值与最小二乘的Ratio值分布统计如图2所示。

图2 不同虚拟权条件下的Ratio值与最小二乘的比较

从图2可以看出，加入虚拟观测值后可以增大整周模糊度检验的ratio值，增加可靠性。当ratio门限值取2时（Frei and Beutler，1990），最小二乘法有43个历元不能通过raito检验，而增加虚拟观测方程后不能通过检验的分别为：8、11、32个历元。但是，为了验证虚拟权的正确与否，更重要的是要检验加入的虚拟观测值是否会引入误差，即：只用最小二乘法时，ratio检验可以通过，而加入虚拟观测值时，反而不能通过。

为进一步验证pv取值是否合理，通过其不同值的选择进行解算后的比较，结果如表1所示。

表1中，序号栏表示无约束条件下不能通过ratio检验（由于门限值取2过于保守，比较了门限值取1.5）的观测值的序号，历元号则表示观测值所在的历元。约束值表示所加的不同约束状况，以及不同约束状况下的ratio值。阴影部分表示加了约束后依然不能通过ratio检验的历元。从表中可以看出加了约束以后，不能通过ratio检验的历元明显减少，而且不会引入新的误差。但是所加的约束必须要适当，如果所加约束过紧，则会引入新的不能通过ratio检验的历元，严重时甚至会得到错误的解算结果。如当Z方向的虚拟观测权取1.0e－3，历元497、500、596也不能通过ratio检验，而实际上这些历元的解算在正常情况（不加约束）下没有问题。反之，如果所加约束过松，如取虚拟观测权为1.0e－5，虽然对计算的结果也有所改善（不能通过ratio检验的历元数为12，小于不加约束条件下的14），但是效果不是很明显。因此，约束的关键就是选取适当的虚拟观测权。

表1 不同条件下不能通过ratio（阈值＝1.5）检验的历元数比较

4 结 论

从以上分析结果可以看出，利用建立虚拟观测方程的方法可有效用于动态定位的参数解算中，且具有以下特点：

1）可以有效利用现有的信息，包括先验方差、位置信息等，有效改进定位的解算结果；

2）利用虚拟观测值可以使模糊度检验时的raio值明显增大，增加检验结果的可靠性；

3）虚拟观测方程的引入，并不会畸化和扭曲参数的解算结果。这对于GPS动态定位具有重要的意义。

［1］周忠谟，易杰军.GPS测量原理与应用［M］.北京：测绘出版社，1999：21－35.

［2］刘大杰，施一民，过静珺.全球定位系统（GPS）的原理与数据处理［M］.上海：同济大学出版社，1996.

［3］许其凤.空间大地测量学［M］.北京：解放军出版社，2001.

［4］刘基余.GPS卫星导航定位原理与方法［M］.北京：科学出版社，2008：147－152.

［5］何海波.高精度GPS动态测量及质量控制［D］.郑州：信息工程大学，2002：48－51.

［6］郑冲.双星/道路组合定位技术及基于双星定位系统的快速定向技术研究［D］.长沙：国防科大，2005：27－35.

［7］S YOON.Real－time attitude determination using the global positioning system［D］，Ph.D.Dissertation，Auburn University，June 1999，28－29.

［8］P.G.QUINN，Instantaneous GPS Attitude Determination.In：Proceedings of ION GPS 1993［J］，Salt Lake City，UT.September 22－24，1993，603－615.

［9］UDAYAN V.BHAPKAR，ALAN G.EVANS，etc.，GPS/INS Attitude Determination Using Precise Kinematic Positioning［C］.Proceedings，ION GPS 1999，Tennesee，US：ION，1999：1989－1998.