二次B样条修正VTEC多项式模型研究

周玉娟，岳桂昌

（河海大学 地球科学与工程学院，江苏 南京 210098）

对于GPS等无线电卫星导航定位的用户而言，电离层延迟误差是影响导航定位精度和准确度的主要误差源之一，电离层总电子含量及其变化不但是电离层形态学研究的重要资料，也是精密定位、导航和电波科学中电离层修正的重要参数［1］。

电离层VTEC多项式模型是一个广泛用于模拟区域天顶方向电离层总电子含量（VTEC）时空变化的模型［2］。该模型忽略了VTEC的局部特性，限制了建模精度，也不利于分析建模方法对模型求解精度的影响。为此，本文基于数值逼近理论，提出了一种有利于克服多项式函数模型的上述不足和进一步提高TEC建模精度的新模型——电离层VTEC多项式展开模型和B样条函数的组合模型。

在电离层VTEC多项式函数模型的解算过程中，拟合曲面的光滑度和逼近精确度之间存在着矛盾。这种矛盾的解决方法是首先得到一个比较粗糙的概略初值，通过对概略初值进行修正以得到更精确的逼近函数。在该模型的建模过程中，将VTEC分成概略初值和修正值两部分，模型表达式为［3］

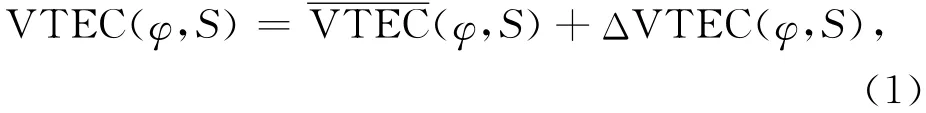
或

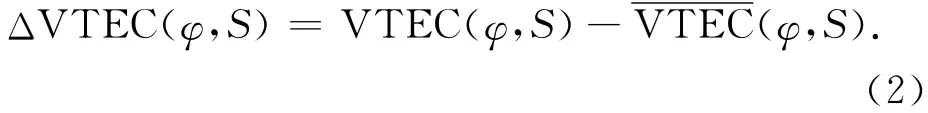
1 VTEC多项式模型求解概略值原理

多项式函数模型将VTEC看作是纬度差φ－φ0和太阳时角差S－S0的函数，用一个规则的曲面来拟合各穿刺点处的VTEC值，其具体表达式为［4］

式中：nmax，mmax为φ和S多项式的泰勒展开式中的最大维数，Enm为VTEC多项式函数模型的系数，φ0为测区中心点的地理纬度，φ为穿刺点或者星下点的地理纬度，S0为测区中心点在该时段中央时刻t0时的太阳时角，S为穿刺点或者星下点的太阳时角，t为观测时刻（世界时），λ为穿刺点或者星下点的地理经度，λ0为测区中心点的地理经度。

利用载波相位建立VTEC的观测方程为

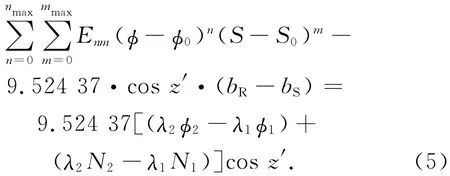
式中：z′为地心至穿刺点方向与接收机至卫星方向的夹角，即穿刺点处的天顶距，bS，bR分别为载波相位观测的卫星硬件延迟和接收机硬件延迟。

通常nmax取1～2，mmax取2～4，VTEC多项式函数模型对单层模型的高度H在计算中一般取300～500km。每个参考站上每观测一颗卫星、一个历元就有一个观测方程，按最小二乘法解得各待定参数Enm和bS，bR，从而建立起该时段的电离层延迟模型。

2 二次B样条模型求解修正值原理

根据B样条曲面的定义，将修正部分用B样条函数模型表示为

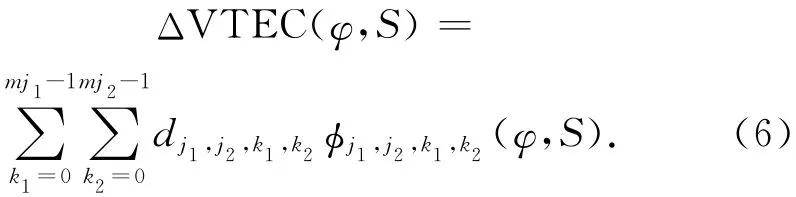
式中：mji＝2ji＋2，j1，j2为阶数，dj1，j2，k1，k2为模型系数，φj1，j2，k1，k2（φ，S）为二维尺度函数，φ为穿刺点或者星下点的地理纬度，S为穿刺点或者星下点的太阳时角，φj1，j2，k1，k2（φ，S）可利用张量积方法展开为

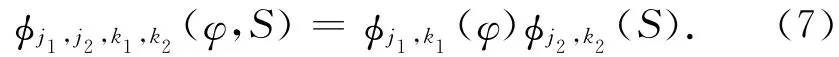
尺度函数φj1，k1（φ），φj2，k2（S）可表示为二次样条函数，即

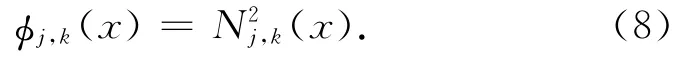
其中可由式（9）推导得到

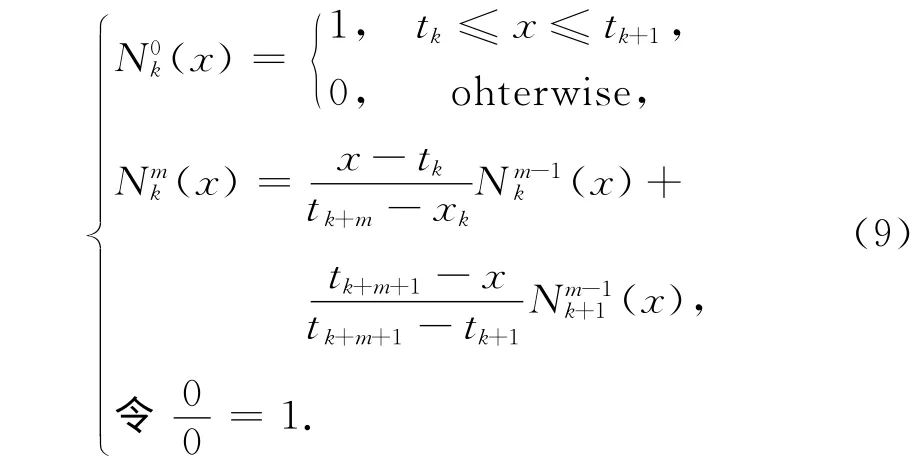
其中：tk为非减节点序列，k＝0，1，…，mj＋2。

为避免区域模型在区间［0，1］的首位节点处产生边界效应，将前3个节点设置为0，最后3个节点设置为1，其余节点设置为等间距。组成节点向量［0，0，0，tj，0，tj，1，…，tj，mj＋1，tj，mj＋2，1，1，1］。这 就 意味着φj，k（x）的变量x的值位于0和1之间，所以S和φ需要做如下的归化处理：

式中：Smin，Smax和φmin，φmax表示区域模型覆盖的范围。

于是，式（6）可转换为

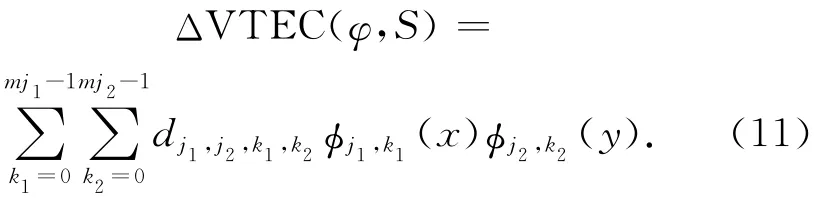
利用载波相位建立VTEC的观测方程为

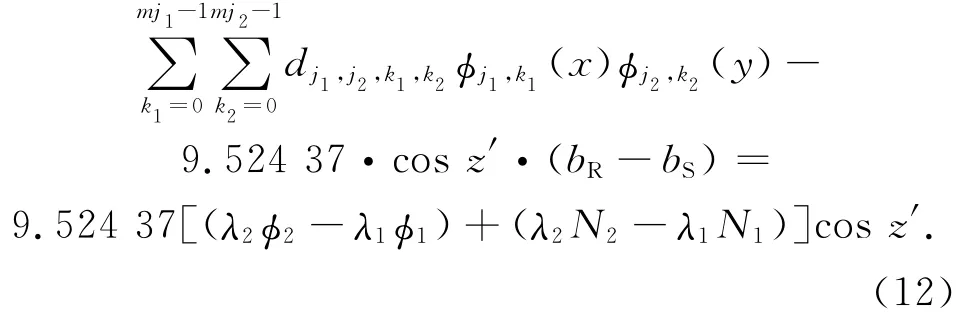
对于式（6）的B样条函数修正模型，选择mj1＝mj2＝2，方程有36个待估参数，通过2h的观测数据即可建立对应的模型。

3 模型解算

通过式（5）、式（12）建立的模型误差方程为

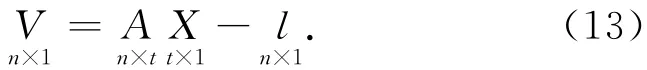
其中：待估参数为X，A为系数矩阵，P为权阵。

对于VTEC多项式模型，基于最小二乘原理直接解算，其解为

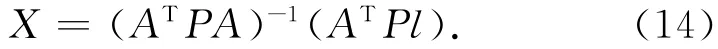
精度评定

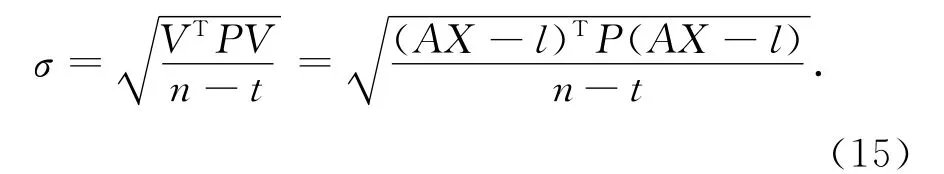
在二次B样条模型解算的过程中，由于GPS观测数据采样率较高以及模型构造的原因，方程呈现严重病态，使用最小二乘估计无法得出正确结果。综合各种因素，采用基于L曲线法选取岭参数对模型进行岭估计解算，其解的表达式为

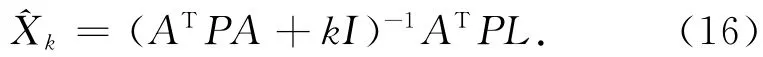
式中：k＞0为岭参数，通过L曲线法求得，岭估计的均方误差为

4 模型试验结果与分析

二次B样条修正多项式模型的分析采用南京周边的8个参考站，2009年年积日001的数据，以单站模式进行2h时间间隔进行VTEC计算。以NJLS和NJLT站为例，利用多项式函数模型、二次B样条修正多项式模型解算的VTEC见图1。

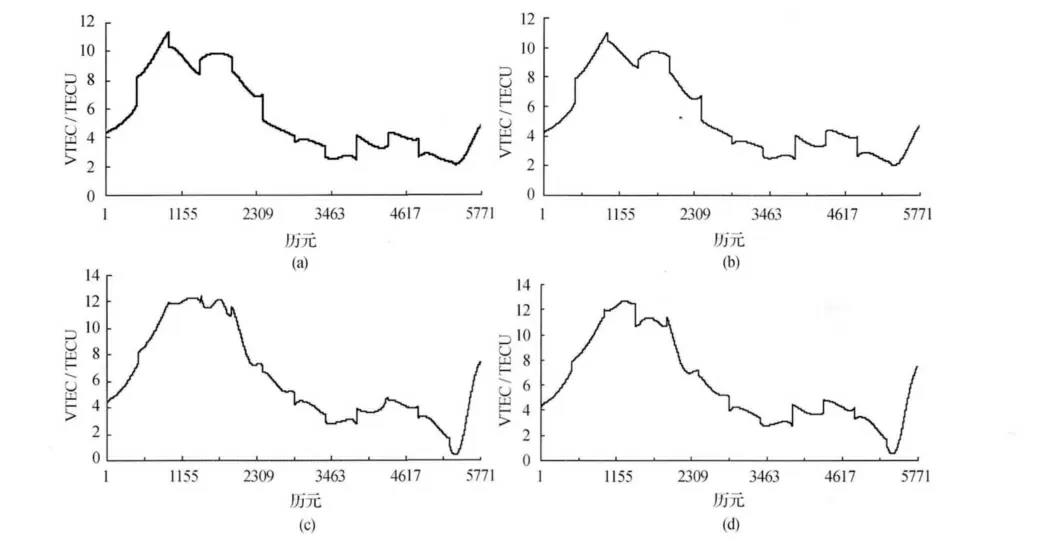
图1 多项式函数模型及B样条函数修正模型解算结果

图1（a）、图1（b）分别为NJLS和NJLT的多项式函数模型解算结果，图1（c）、图1（d）分别为NJLS和NJLT的B样条函数修正模型的解算结果。可以看出，两种模型的解算结果整体趋势是一致的，在数值上也比较接近，而多项式函数模型解算的各时段VTEC存在明显的不连续性。在经过B样条函数修正后的VTEC可以使各时段间的不连续性得到改善。但由于B样条函数修正模型是基于多项式函数模型结果的进一步修正，另外，由于观测数据的质量等原因使得B样条函数修正模型未能完全解决各时段间的VTEC的不连续性。对于各时段间VTEC不连续性的问题，本文采取各时段连接点的VTEC按解算精度取加权平均值。

由表1可知，B样条函数修正模型的解算的VTEC精度要高于多项式函数模型解算的VTEC精度。采用VTEC的B样条函数修正模型不仅可以更好地模拟各时段的VTEC，而且可以有效缓解VTEC的时段间的不连续性。

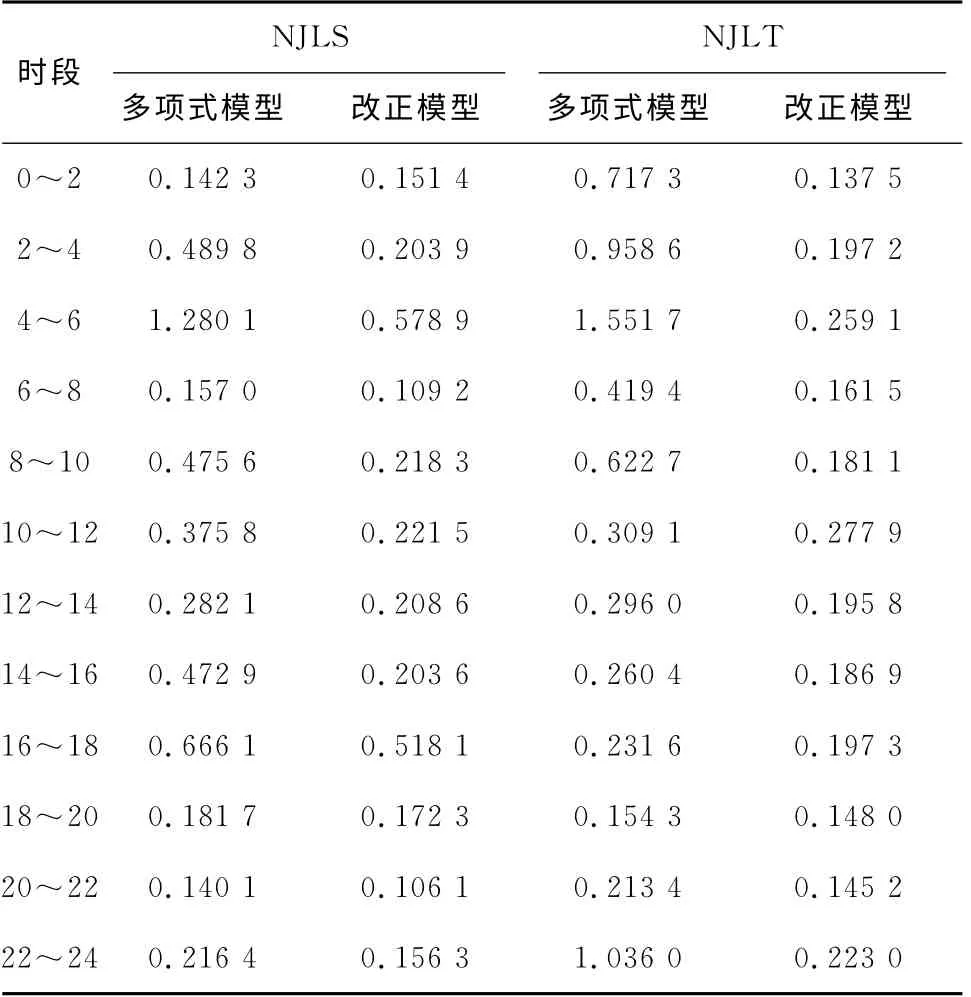
表1 多项式函数模型与B样条函数修正模型解算精度 TECU

5 结束语

B样条函数修正模型将VTEC分为概略值和修正值两部分进行解算。它保持了VTEC的局部特性，因而精度和可靠性均好于多项式函数模型，特别是可以克服利用多项式函数模型拟合区域VTEC时可能出现负值等情况，并且解决了拟合曲面的光滑度和逼近精确度之间存在的矛盾。采用L曲线法对模型进行岭估计解算，效果良好。B样条函数修正模型更能反映VTEC的实时性的特征，同时可以缓解多项式函数模型解算的各时段VTEC的不连续性。

［1］宋茂忠，王永澄.电离层对普通GPS和位置差分GPS定位误差的影响［J］.南京航空航天大学学报，1994，26（6）：782－788.

［2］张小红，李征航，蔡昌盛.用双频GPS观测值建立小区域VTEC模型研究［J］.武汉大学学报：信息科学版，2001，26（2）：140－144.

［3］M Nohutcu，M O.Karslioglu，M.Schmidt.B－spline modeling of VTEC over Turkey using GPS observations［J］.Journal of Atmospheric and Solar－Terrestrial Physics，2010，72，：617－624.

［4］Rolf Dach，Pierre Fridez.Bernese GPS SoftWare Version 5.0［M］.Astronomica Institute，2007：260－261.

［5］丁士俊，靳祥升.平差不适定问题解的性质与正则参数的确定方法［J］.测绘科学，2006，31（2）：22－24.

［6］Rodriguez G，Theis D.An Algorithm for Estimating the Optimal Regularization Parameter by theL－curve［J］.Rendiconti di Matematica，2005，25（1）：69－84.

［7］王振杰，欧吉坤.用L－曲线法确定岭估计中的岭参数［J］.武汉大学学报：信息科学版，2004，29（3）：235－238.

［8］陈希孺，王松桂.近代回归分析［M］.合肥：安徽教育出版社，1987.