MKZ 型算子中心矩的明确上界估计

雷 阳，叶培新，宋占杰

(1. 天津大学理学院，天津 300072；2. 南开大学数学学院，天津 300071)

最近，Meyer-König 和 Zeller 算子(简称 MKZ 算子)及其变型算子的逼近问题成为算子逼近的一个热点问题[1-16]，然而进一步研究需要给出其各阶矩的明确上界估计，笔者主要从基础理论方面进行了一些研究.

1 基础研究

1960 年，由 Meyer-König 和 Zeller 受若干Bernstein 型算子的构造启发给出一类 Meyer-König和 Zeller 算子[14]，即

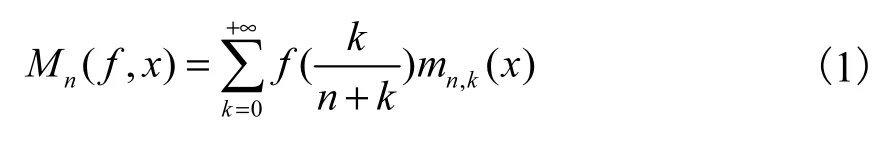
由于算子本身计算复杂度较高，进一步研究成果较少，Becker 和 Nessel 在1978 年才给出算子的二阶中心矩估计．

命题 1.1[17]Meyer-König 和 Zeller 算子的二阶中心矩满足不等式

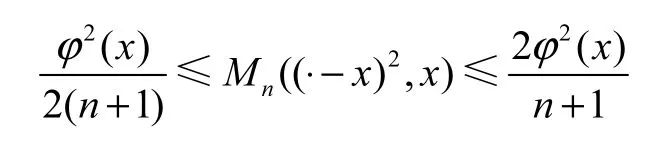
显然，这个估计结果很粗略，其上下界相差3 倍.

探索其中心矩的工作一直没有间断，Abel[18]在1995 年给出Meyer-König和Zeller 算子的明确二阶中心矩估计，从本质上改进了上述结果．

命题 1.2[18]Meyer-König 和Zeller 算子的二阶中心矩为

高阶矩一般表达式的计算比较困难，Guo 和Qi[19]在2007年用归纳法给出了 Meyer-König 和Zeller 算子的各阶中心矩的一个上界估计．

命题 1.3[19]设r 为正整数，n 2r＞ ，且ϕ(x)=则有

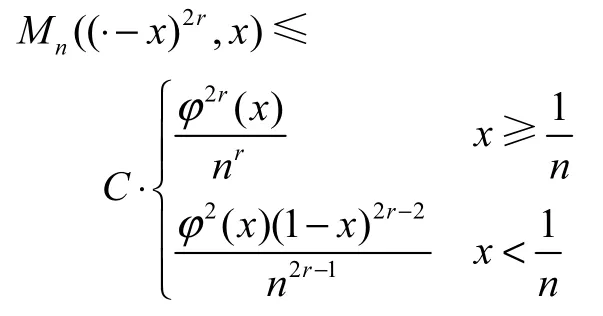
式中C 为不依赖于x 和n 的常数.

由于上述结果只是给出常数C 的存在性，在逼近估计式中有时会带来不便．所以，本文在上述结果的基础上，进一步明确给出C 的取值，从而给出确定的上界．

定理 1.4设r为正整数，n ＞2r，且ϕ(x)=则有

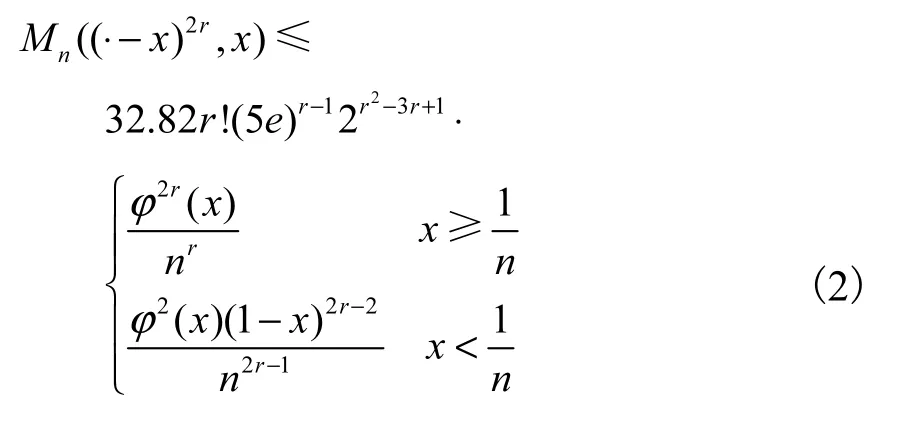
2 引理及其证明

引理2.1[17]对于，n≥2 ，x ∈[0,1]，有

引理2.2对于b ≤a，∀ x ，则有

证明：当b ≤x ≤a 时，b−x≤0≤a −x .

则

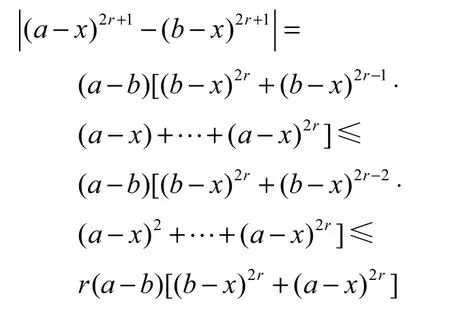
当x≤b≤a 时，0 ≤b−x≤a −x

则

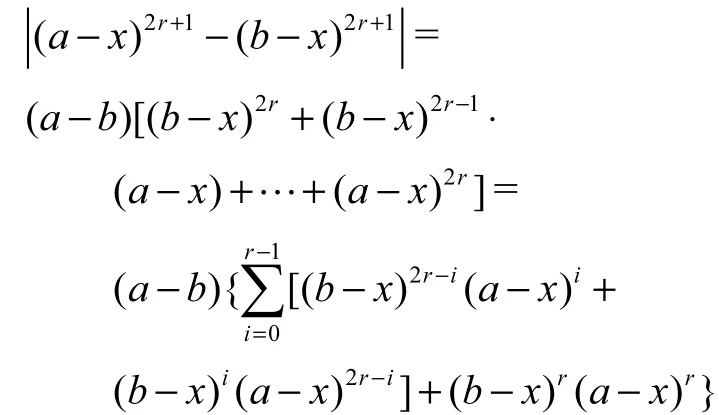
所以式(4)成立.

当b ≤a ≤x 时，同理有式(4)成立.

综上，命题成立.

引理 2.3(Stirling 公式)对于n N+∈，有，其中

引理 2.4设r为正整数，n＞2r，且ϕ(x)=则有

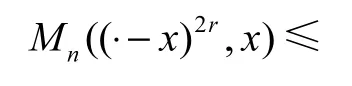
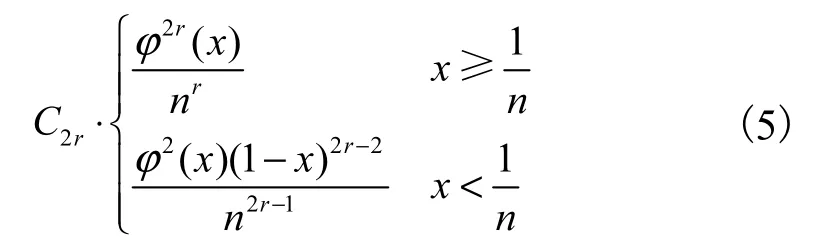
其中，C2=1.5，当r ≥ 2时，满足递推公式

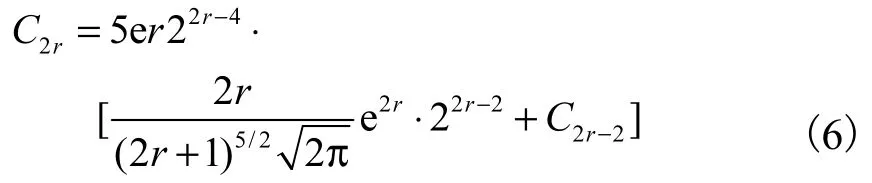
证明：由引理2.1 知

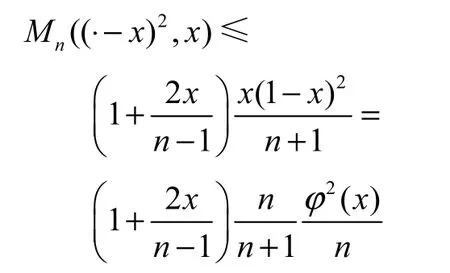
最后一步是因为由条件有n≥ 3，所以 C2= 1.5.

下面假设已知 C2r，接下来证对 C2r+2有命题中的递推公式，假设n＞ 2 r+2

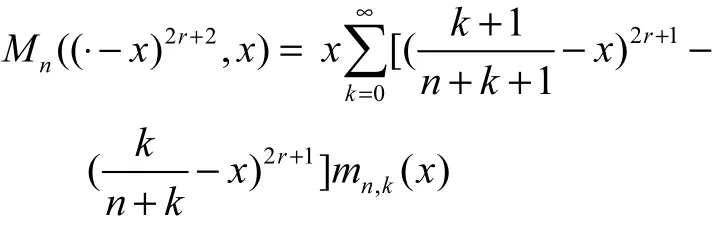
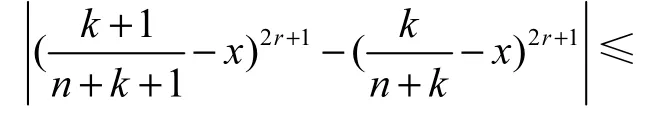
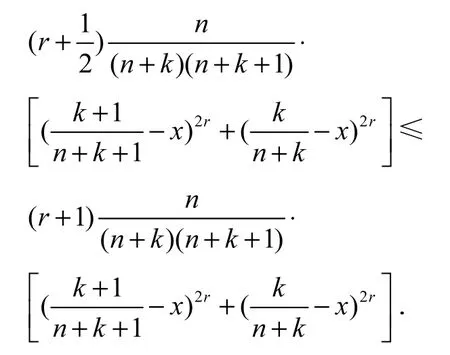
所以有

考察

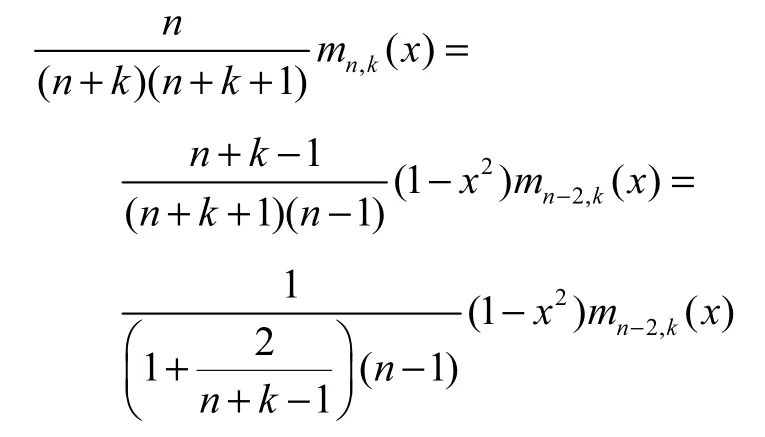
因为n≥2r+2，所以n≥ 5时有

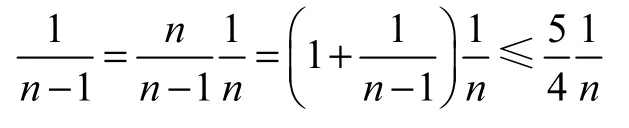
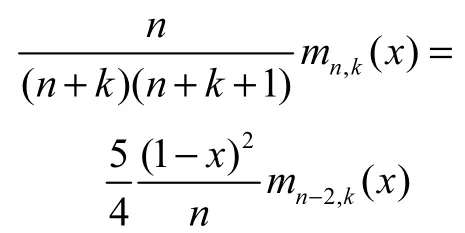
即Mn((·−x)2r+2,x)≤

考察

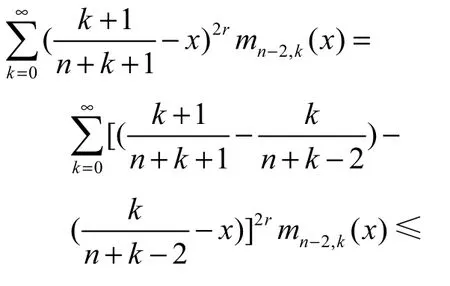
对于

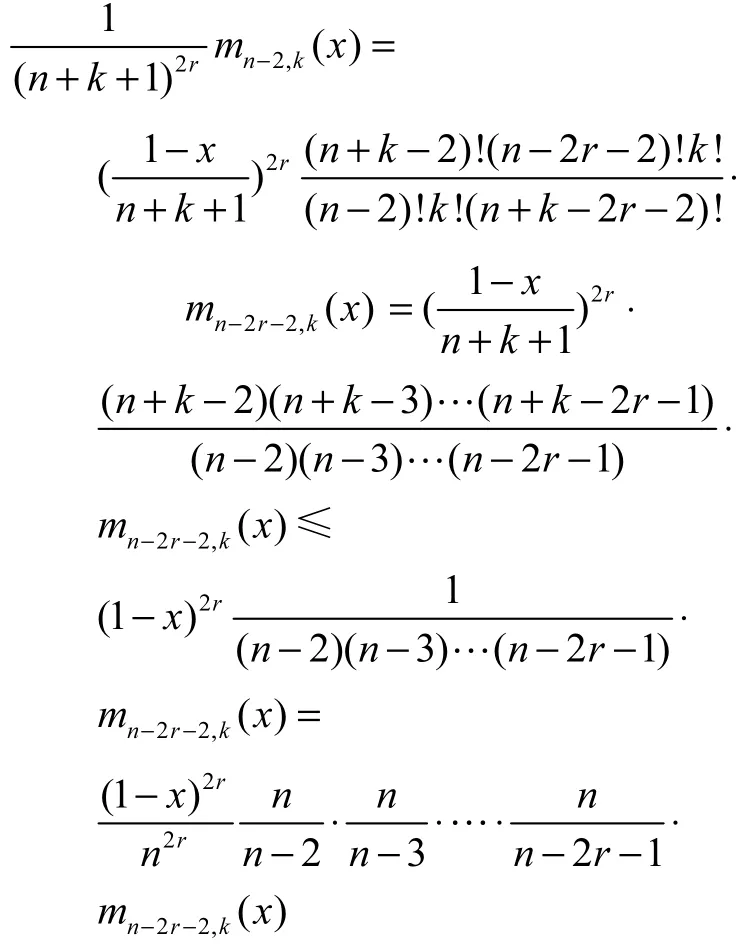
因为n＞2r+2，即n≥2r+3

所以

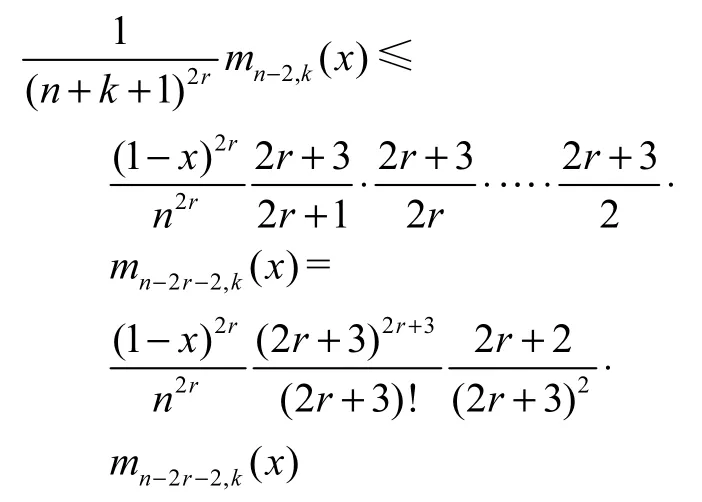
再由引理2.3，可知

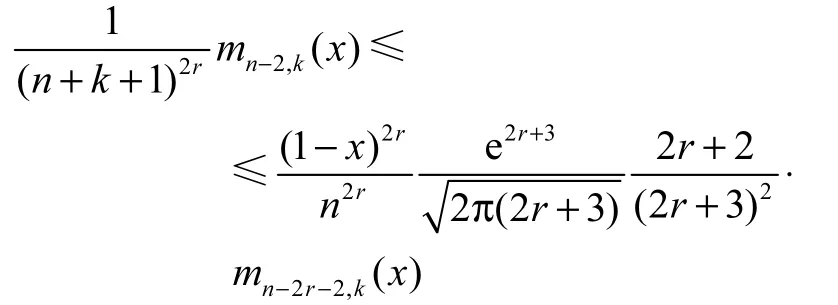
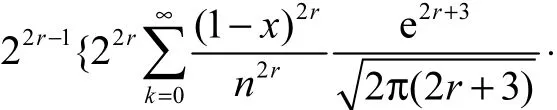
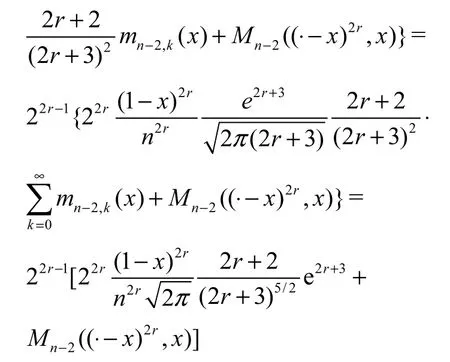
即是

由假设知

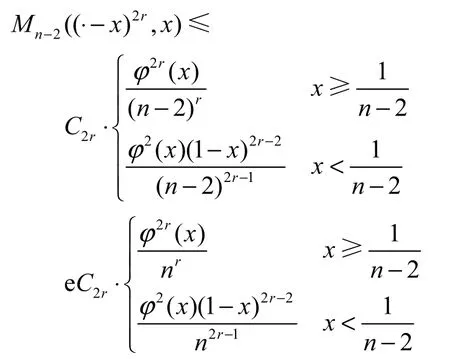
这里 a～ b 意味着存在一个常数D ，使得

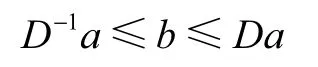
事实上有

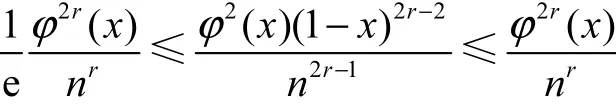
于是

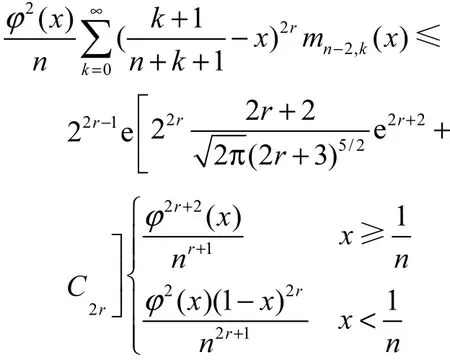
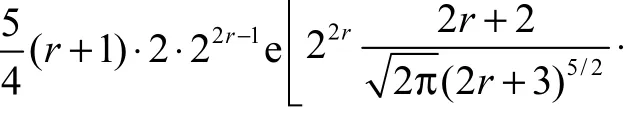
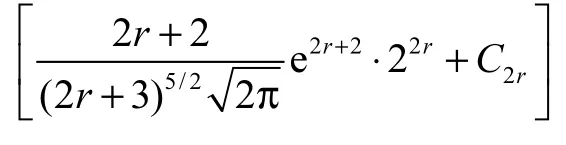
假设成立，引理得证.

3 主要结果及其证明

下面证明定理1.4

证明：利用引理2.4，可知

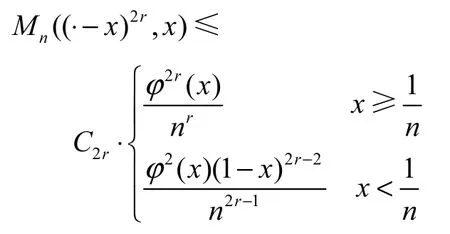
其中，C2=1.5，当r ≥ 2时，满足递推公式

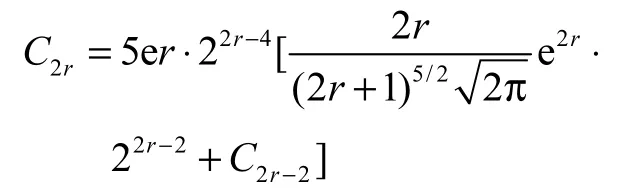
当r≥5 时，

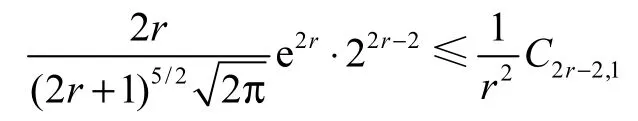
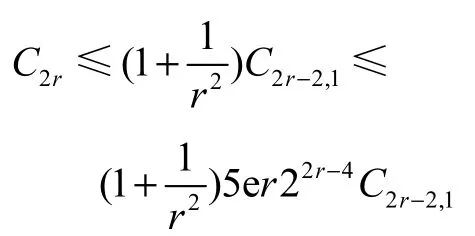
利用引理2.4，可知在 r=1,2,3,4时，

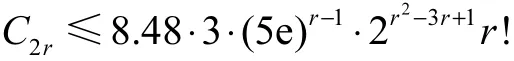
推论3.1设m 为偶数，m≥4，n＞m，且 ϕ(x)=则有

证明：利用定理1.4

再由引理2.3，可知

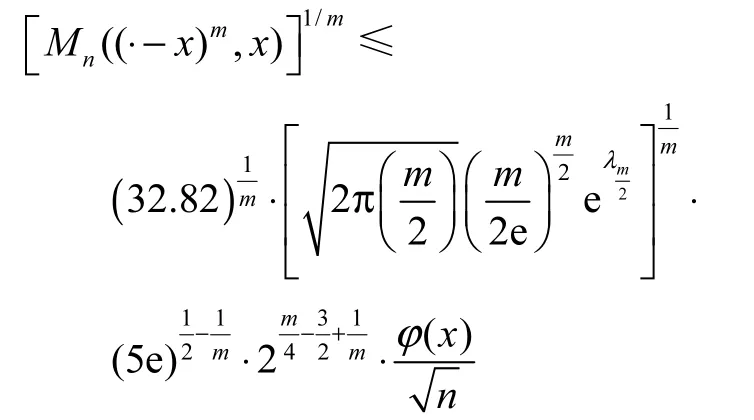
当m≥4 时，有

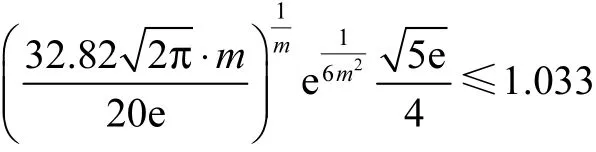
4 结 语

MKZ 算子及其变型算子的逼近问题是算子逼近的一个热点问题，在研究各阶矩过程逼近方面有一定的理论意义和应用价值.本文给出了 MKZ 型算子各阶矩的明确上界估计，给出的方法可以用于其他类似算子中心距的上界估计，同时上述概率型算子的中心距的上界估计为进一步研究其逼近性质提供了重要工具.

［1］Bede B，Coroianu L，Gal S G. Approximation and shape preserving properties of the nonlinear Meyer-K˙o˙nig and Zeller operator of max-product kind[J].Numerical Functional Analysis and Optimization，2010，31(3)：232-253.

［2］Bustamante J，Martinez-Moreno J，Quesada J M. An application to the MKZ-operators of generalized convexity on ECT-systems[J].Journal of Mathematical Analysis and Applications，2008，342(1)：497-502.

［3］Dogru O，Orkcu M. Statistical approximation by a modification of q-Meyer-Konig and Zeller operators[J].Applied Mathematics Letters，2010，23(3)：261-266.

［4］Dogru O，Orkcu M. King type modification of Meyer-K˙o˙nig and Zeller operators based on the q-integers[J].Mathematical and Computer Modelling， 2009 ， 50(7/8)：1245-1251.

［5］Doğru O ， Muraru C. Statistical approximation by Stancu type bivariate generalization of Meyer- K˙o˙nig and Zeller type operators[J].Mathematical and Computer Modelling，2008，48(5/6)：961-968.

［6］Guo S S，Liu L X，Chen H. Approximation by generalized Meyer- K˙o˙nig and Zeller type operators[J].Studia Scientiarum Mathematicarum Hungarica， 2009 ， 46(2)：239-261.

［7］Guo S S，Liu L X，Wang Z M. Pointwise approximation by Meyer- K˙o˙nig and Zeller operators[J].Numerical Functional Analysis and Optimization，2008，29(7/8)：770-778.

［8］Guo S，Li C，Qi Q. Strong converse inequalities for Meyer- K˙o˙nig and Zeller operators[J].Journal of Mathematical Analysis and Applications， 2008 ，337(2)：994-1001.

［9］Qi Q L，Liu J. Pointwise approximation theorems for Meyer- K˙o˙nig and Zeller-Durrmeyer operators[J].Publicationes Mathematicae Debrecen，2008，73(1/2)：101-117.

［10］Ozarslan M A，Duman O. Approximation theorems by Meyer-Konig and Zeller type operators[J].Chaos，Solitons & Fractals，2009，41(1)：451-456.

［11］Zeng X M，Gupta V. Approximation by the Bezier variant of the MKZ-Kantorovich operators in the case α＜1[J].Central European Journal of Mathematics，2009，7(3)：550-557.

［12］Zeng X M，Lian B Y. An estimate on the convergence of MKZ-Bezier operators[J].Computers and Mathematics with Applications，2008，56(12)：3023-3028.

［13］Zeng X M. On the rate of approximation of Meyer-Konig and Zeller operators[J].Journal of Computational Analysis and Applications，2008，10(4)：527-535.

［14］Meyer- Ko˙˙nig W，Zeller K. Bernsteinsche potenzreihen[J].Studia Mathematica，1960，19(1)：89-94.

［15］Song Zhanjie，Yang Zhendong，Ye Peixin. Estimates of central moments for one kind of exponential-type operators[J].Transactions of Tianjin University， 2011 ，17(2)：85-88.

［16］宋占杰，叶培新. 随机信号 Feller 概率型算子[J]. 天津大学学报，2011，44(2)：180-183.Song Zhanjie，Ye Peixin. Approximation of random signals by Feller-type probabilistic operators[J].Journal of Tianjin University， 2011 ， 44(2) ： 180-183(in Chinese).

［17］Becker M，Nessel R J. A global approximation theorem for the Meyer-König and Zeller operators[J].Mathematische Zeitschrift，1978，160(3)：195-206.

［18］Abel U. The moments for Meyer-König and Zeller operators[J].Journal of Approximation Theory， 1995 ，82(3)：352-361.

［19］Guo S，Qi Q. The moments for Meyer-König and Zeller operators[J].Applied Mathematics Letters，2007，20(7)：719-722.