数控机床主轴热特性分析
姜 杉,赵志刚,孙明陆,郭建慧,于 红
(1. 天津大学机械工程学院,天津 300072;2. 天水星火机床有限责任公司,天水 741024)
数控机床误差主要包括几何误差、热误差、切削力误差和控制误差等.其中,热误差占总误差的40%~70%左右[1].而机床主轴作为数控机床的核心部件,是热误差的主要误差源.因此,研究机床主轴热变形特性对实施热误差补偿控制,提高机床加工精度至关重要,已受到广泛重视.
建立高精度和高鲁棒性的热误差预测模型是热误差补偿中的最关键部分.目前建模方法主要有最小二乘法、BP 神经网络、RBF 神经网络、灰色系统理论和遗传算法等[2-6].因此,研究机床主轴热源、温度场和热变形的变化规律及动态特性是降低热变形误差、提高机床加工精度所必须考虑的.浙江大学陈兆年等[7]研究了机床热态特性实验技术并对主要类型的机床热态特性进行了分析.数值计算是分析机床热变形的另一有效方法[8-10].为此,笔者通过传热学的理论,分析热弹性现象产生的原因,并通过一维主轴传热有限元分析和实验进一步验证热动态特性的存在及变化规律.
1 热弹性效应的理论分析
考虑如图 1 所示的一维主轴.主轴左端紧固,右端自由,长度为 L,与空气的综合散热系数为Hf,空气温度为fθ,Q(t) 为从左端流入的周期变化热源.一维主轴的热传导方程为
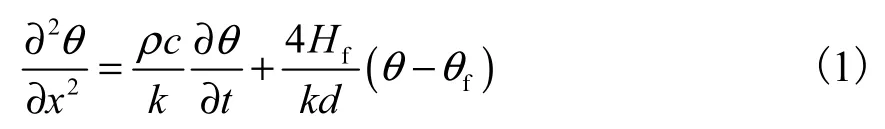
式中:θ(x,t)为一维主轴上某一点的温度,是时间t 和位置坐标x的函数;k 为热传导率;ρ为主轴密度;c为比热容.
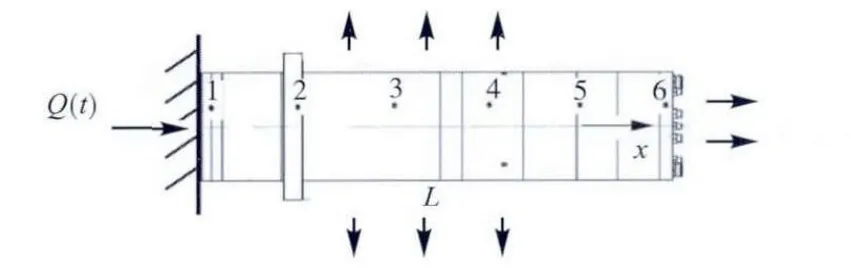
图1 一维主轴传热模型Fig.1 One-dimensional spindle heat tansfer model
一维主轴与周围空气的热交换主要为对流传热.当主轴与空气之间的温差比较小时,热交换也比较小.暂不考虑主轴与周围空气的热交换,式(1)变为

若左端输入周期变化的热流,左端处的温度函数为
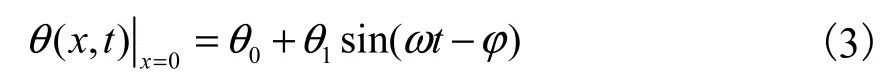
将式(3)作为式(2)的边界条件,可求得式(2)的解为
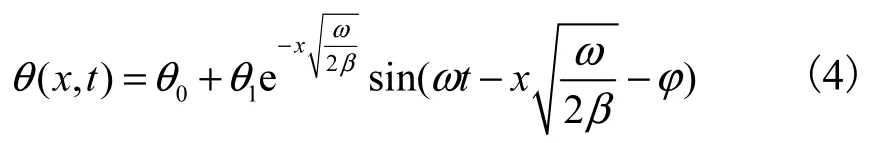
定义时间t0的温度θ(x,0t)为温度波,由式(4)可知,温度波的振幅随x 增大而递减,大小为

温度波的波长随t 的增大而递增,大小为

随着时间t 的增加,温度波由左向右移动,波速为

2 一维主轴热误差有限元分析
主轴热变形滞后于温度的变化,热流输入与热弹性变形具有不同的时间常数.现将主轴模型简化为一维模型,分析其热变形特性,如图1 所示.
其中,模型左端轴向固定,右端自由伸长.左端面设置热流Q(t) 输入,其余各表面与外界进行对流传热,热对流系数为Hf(t) .模型表面均布 6 个温度和位移观测点,即点 1、2、3、4、5、6.其中点 1 靠近热源处,点 6 位于模型右端.模型尺寸与材料属性如表1 所示.

表1 一维主轴模型参数Tab.1 One-dimensional spindle model parameters
为充分了解一维主轴模型的热变形特性,分析主轴在不同类型热源作用下的温度场与热变形场变化特性,模型左端施加 3 种不同类型的热源.其中,热源强度及工作周期如表2 所示.

表2 3组仿真热源强度值Tab.2 Three groups of simulation of heat strength value
2.1 简单温度场热弹性分析
一维模型观测点温度及位移值变化如图 2 和图3 所示.由图2 可知:①点1 靠近热源处,温升较高,对热源的反应最为迅速,前1000 s 模型左端有定值热源输入,点 1 的温度值以凸函数形式增加,后1200 s停止加热,温度值以凹函数形式下降,最后趋于平缓;②点 2~点 6 的温度值对热源反应速度依次减慢,其中,点6 反应最为缓慢,温升较小,且在停止加热后,仍有一段时间处于上升状态,反映了温升对热源变化的滞后性;③点1~点6 各相邻点的温度差值依次减小,表现出热流传递的滞后性.由图 3 可知:①点2 与点1 之间位移差值最大,故此段热伸长量最大,与此段温度较高一致,由左向右,各点之间热伸长量逐渐减小;②所有轴向热变形累加至模型右端点6 处,该点热位移最大,可代表一维主轴整体轴向热伸长量.
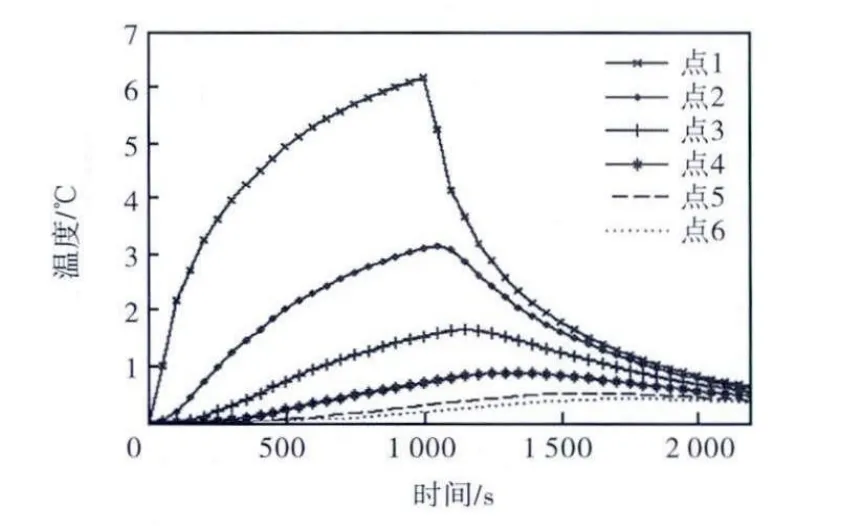
图2 仿真1观测点温度曲线Fig.2 Temperature curves of observation points in simulation 1

图3 仿真1观测点位移曲线Fig.3 Displacement curves of observation points in simulation 1
2.2 复杂温度场热弹性分析
改变模型热源类型,仿真2 和3 结果如图4~图7 所示.当模型左端输入为正弦类型或方波类型热流时,各点温度及位移的变化相对于热源的滞后性更为明显.各点温度值与整体轴向热伸长量之间的关系更为复杂,表现出高度非线性和滞后性,且其相互关系根据热源的不同而变化.点 2 的温度值与整体轴向热伸长量之间的类线性关系也发生变化,但整体线性度较好.从仿真 2 和仿真 3 进一步证明温度场分布是热弹性现象产生的原因之一,并反映了热弹性的相关特性.
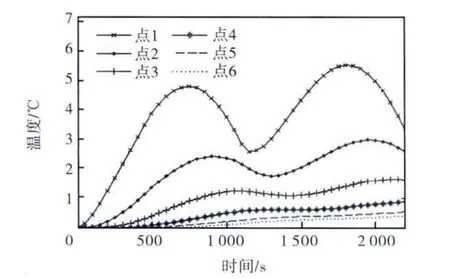
图4 仿真2观测点温度曲线Fig.4 Temperature curves of observation points in simulation 2

图5 仿真2观测点位移曲线Fig.5 Displacement curves of observation points in simulation 2
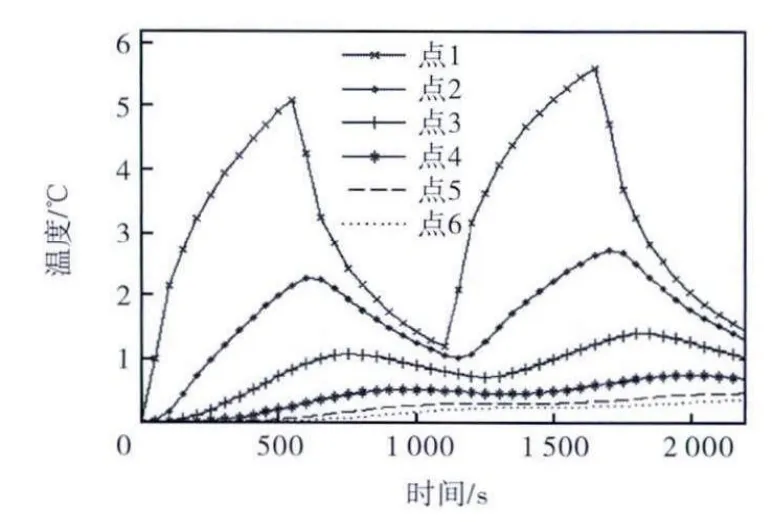
图6 仿真3观测点温度曲线Fig.6 Temperature curves of observation points in simulation 3

图7 仿真3观测点位移曲线Fig.7 Displacement curves of observation points in simulation 3
2.3 复合温度场分析
改变模型所处环境,进行仿真 4,以研究复合温度场对热弹性特性的影响.模型尺寸与对流系数保持不变,由一端加热改为两端加热,其加热强度为Q(t)=10 W,前1000 s 进行加热,后1200 s 进行冷却,物理模型如图8 所示.
由图9及图10可知,由于物理模型的对称性,点1与点6、点2与点5、点3与点4的温度值基本相同.靠近热源的点1及点6的温度变化超前于整体热变形,远离热源的点3及点4 温度变化滞后于整体热变形,而点2 及点5 温度变化与整体热变形基本保持线性关系.

图8 主轴一维模型两端加热Fig.8 Heating of two ends of the one-dimensional spindle model

图9 仿真4观测点温度曲线Fig.9 Temperature curves of observation points in simulation 4
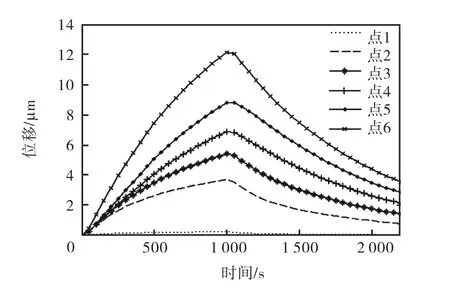
图10 仿真4观测点位移曲线Fig.10 Displacement curves of observation points in simulation 4
3 热误差实验验证
测试系统以获得机床主轴关键点的温度和主轴热变形值为实验目的.温度传感器和位移传感器安装在机床上,DAQ 板卡中包含调理电路、保护电路和模数转换器等.计算机安装有 DAQ 板卡驱动和数据采集程序.根据已选择的各硬件部分,配置相应的数据线与电源线,搭建起测试实验的硬件平台,采用国家标准(GB/T17421.3—2009)规定中的五点法测量机床主轴热误差,如图11 所示.

图11 机床主轴热特性数据采集实验Fig.11 Data acquisition experiment of thermal characteristics of spindle
搭建完测试实验硬件平台与软件平台后,设置采样率为1.00 采 样数 /s ,主轴最大转速为2 000 r/min ,测试主轴的转速由不同的主轴转速构成,每种主轴转速做2~15 min 运行,期间做15 min 停歇来代表典型的加工条件.速度图谱如图12 所示.
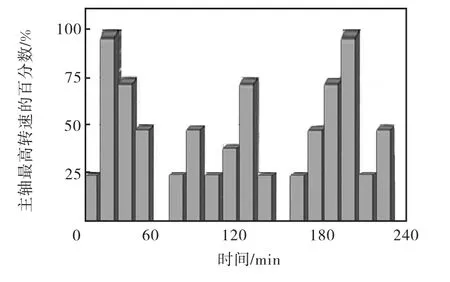
图12 热变形实验主轴速度图谱Fig.12 Map of spindle speed in thermal deformation experiment
因机床实际运行过程中,径向误差受主轴同轴度影响较大,难以测试出由热变形引起的误差,故本测试实验以测试机床主轴轴向热变形为目的.轴向误差主要由热误差组成,在空转的情况下最为显著.选取如图1 所示有限元分析的点1 和点3 的对应位置分别进行测试,实验前150,min 结果如图13 所示:初始状态主轴温升较快,轴向热变形增加,导致轴向误差也逐渐增加;近热源观测点1 温度波和热变形幅值都大于远观测点3 为幅值,与前面的理论分析结果一致;随着时间的增加,温度与轴向热变形趋于稳态,但实际测试显示,温升-热变形不是绝对的稳态,热变形的变化总是超前或滞后于温升的变化,与有限元分析验证结果吻合;测试时间增加到 150,min,实验结果依然与有限元分析吻合,说明在热平衡状态下,热弹性现象存在,如何有效减少数控机床主轴热弹性现象,对于提高机床主轴精度有着重要意义.
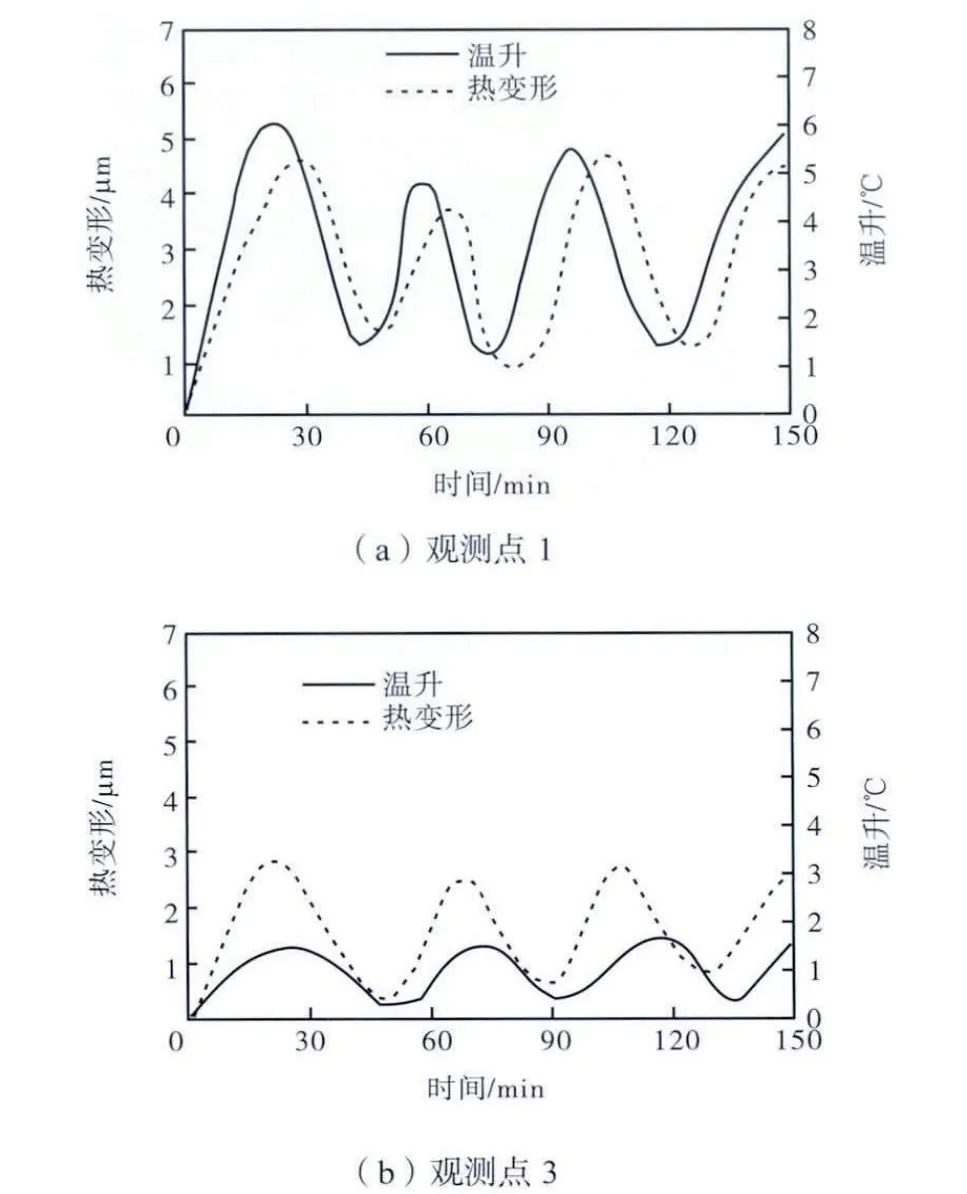
图13 温升-热变形关系Fig.13 Relationship between temperature rising and thermal deformation
4 结 论
(1) 忽略主轴径向方向的热影响,分析一维传热问题,对多维传热和复杂结构的热动态特性分析有指导意义.
(2) 有限元方法是获得机床主轴热变形数值解的有效方法,可以模拟主轴的多种工作情况,方便快捷地获得多节点的物理变量值.
(3) 改变热源类型和数量,一维模型的温度值与热位移以及它们之间的对应关系也发生相应变化.这反映了主轴热特性的复杂性,对热误差建模提出了较高的要求.
(4) 热弹性现象产生的原因之一为温度波,其特征为高度非线性、滞后性和叠加性;机床主轴在热平衡状态下,热弹性现象依然存在,正确解决热弹性问题是提高机床精度的有效方式之一.
[1]Krulewich D A. Temperature integration model and measurement point selection for thermally induced ma chine tool errors [J].Mechatronics,1998,8(4):395-412.
[2]Yang Hong,Ni Juo. Dynamic modeling for machine tool thermal error compensation [J].Journal of Manufacturing Science and Engineering,2003,125(2):245-254.
[3]Wang Yiding,Zhang Guoxiong,Moon K S,et al.Compensation for the thermal error of a multi-axis machining center [J].Journal of Materials Processing Technology,1998,75(1/2/3):45-53.
[4]Choi Hyun-Seung,LeeSun-Kyu. Machining error compensation of external cylindrical grinding using thermally actuated rest [J].Mechatronics,2002,12(5):643-656.
[5]Kang Yuan,Chang Chuan-Wei,Huang Yuanruey,et al. Modification of a neural network utilizing hybrid filters for the compensation of thermal deformation in machine tools [J].International Journal of Machine Tools and Manufacture,2007,47(2):376-387.
[6]李永祥,童恒超,杨建国. 灰色系统理论在机床热误差测点优化中的应用[J]. 机械设计与研究,2006,22(3):78-81.Li Yongxiang,Tong Hengchao,Yang Jianguo. Application of grey system theory in optimizing the measuring points of thermal error on machine tools [J].Machine Design and Research,2006,22(3):78-81(in Chinese).
[7]陈兆年,陈子辰. 机床热态特性学基础[M]. 北京:机械工业出版社,1989.Chen Zhaonian,Chen Zichen.The Basic Study of Thermal Characteristic of Machine Tools[M]. Beijing :China Machine Press,1989(in Chinese).
[8]Zhao Haitao,Yang Jianguo,Shen Jinhua. Simulation of thermal behavior of a CNC machine tool spindle [J].InternationalJournalofMachineToolsand Manufacture,2007,47(6):1003-1010.
[9]Xu Min,Jiang Shuyun,Cai Ying. An improved thermal model for machine tool bearings [J].International Journal of Machine Tools and Manufacture,2007,47(1):53-62.
[10]Zhu Jie,Ni Jun,Shih A J.Robust machine tool thermal error modeling through thermal mode concept[J].Journal of Manufacturing Science and Engineering,2008,130(6):0610061-0610069.

