碰靠定位算法在不规则件排样优化中的应用研究

梁利东 钟相强

安徽工程大学，芜湖，241000

0 引言

排样是指将原材料分割成不同形状的零件毛坯，因此排样问题可抽象为在给定规格的原材料(如板材)中，寻找零件排放最优布局的优化问题。不规则件排样属于最复杂的组合优化问题之一，不仅表现在对不规则零件图形的几何形状描述，还表现在零件形状不规则性将导致零件之间的靠接、判交、控制和评价等处理比较复杂且计算量大。

对于不规则零件排样问题，无论是采用矩形化包络法［1］，还是对不规则零件直接排样如临界多边形法［2-3］等，都需要对零件图形进行判交和碰靠定位处理，以实现零件之间的紧密靠接来提高原材料的利用率。文献［1］中提出了一种典型的不规则排样算法，即将不规则件以矩形件排样结束后，对每个零件进行试探性的移动碰靠测试，通过压缩或挤压过程来减少未利用空间。Hopper等［4］指出了该算法的局限性，因为单个零件的移动可能会导致其他零件的排样位置发生变化，从而难以确定零件的移动方向并影响了计算效率。文献［5］提出的栅格表示法是将板材划分为大小相同的矩形栅格或网格，用它来近似地表示零件的轮廓特征，同时通过判断两个零件图形所占的栅格状态来判断零件间的位置关系，算法实现简单。但这种离散化的表示方法受零件图形的特征或精度要求的局限，对于那些带有复杂弧度或曲线的零件，当需要得到较高的排样精度时，会使得栅格数量剧增，计算量也相应增加，降低了算法的效率。文献［6］在临界多边形(NFP)算法的基础上，提出了重心NFP的概念，通过零件的旋转和移动选择重心NFP中最低重心位置来确定零件的排放定位。这种方法在求解过程中基本上实现了零件最低的定位原则，但需要考虑已排零件与边界形成的轮廓以用来求解NFP的移动碰靠轨迹，计算量较大。

针对以上方法的优劣分析，本文在对每个入排零件进行矩形化预处理来确定其初始位置的基础上，根据最小静矩原理对零件图形进行旋转和移动碰靠来搜索当前零件的最佳排放位置，并以其排样高度和碰靠距离来评价最佳吻合定位，从而实现即时多角度碰靠优化。

1 碰靠定位算法原理

1.1 最低形心碰靠定位方法

零件的排放姿态涉及入排角度的确定，本文采用的最小静矩碰靠定位方法是在保证整体排样高度不增加的基础上，尽可能通过对零件多边形的旋转和平移碰靠处理，使零件多边形的静矩最小。静矩的物理意义表示零件图形相对于板材边界的远近程度或零件之间距离的大小，对于排样问题，选择其最小静矩的入排角度进行排放，从理论上可增加零件与板材边界及零件与零件的接触面，以减少排样过程形成的无效区域，从而增加板材的利用率。图1表示了不同零件在排放中的一般定位(上两个示图)和最小静矩定位(下两个示图)的对比示意。图中的两组示图分别以矩形件和不规则零件为例说明，可见零件在入排过程中以最小静矩碰靠进行定位能有效提高排样区域的有效利用率。特别指出，最小静矩碰靠定位方法是:通过对每个入排零件图形相对于形心的多次旋转及定位碰靠试算，从中选择出静矩最小的排放角度作为该零件的最优入排方案。

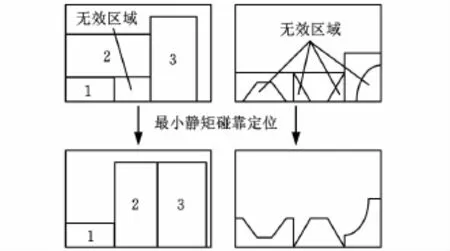
图1 入排零件的最小静矩碰靠定位的排样布局优化

形心及静矩的求解采用正负梯形分割法，即将多边形通过各顶点分割成多个梯形的组合，规定多边形逆时针方向面积为正，顺时针方向面积为负，其中需要注意多边形各边的次序和方向。如图2所示，以五边形为例，多边形面积可表示为

图2 多边形面积计算

在实际下料中，板材一般为均质体(即密度相同)且厚度统一，因此排样零件的形心计算可简化为求解平面多边形的形心，如图3所示，多边形形心求解公式为

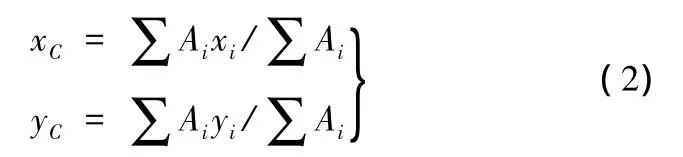
图3 零件多边形的形心坐标

对水平方向的静矩为

式中，Ai为零件图形划分的单元面积;∑Ai为零件多边形的面积;(xi，yi)分别为各单元的形心坐标;Sx为图形对于x轴的静矩或称对于x轴面积的一次矩。

多边形绕其形心进行旋转变换以矩阵表示为

从而得到旋转后的位置坐标为

式中，(x0，y0)为初始坐标;(x，y)为旋转后的坐标;θ为旋转角度。

通常可根据实际情况设置旋转角度间隔Δθ，每个零件以不同入排角度定位后对其静矩值进行比较，取静矩最小实现入排角度的优化。

零件多边形的数据结构定义如下:

1.2 碰靠距离计算

零件碰靠处理的关键步骤是计算两个零件的碰靠距离即零件按照指定的方向与另一个零件发生碰撞时的移动量。一般定义下的零件几何外形轮廓是由若干基本实体或图元(如直线、圆弧、曲线等)组成，碰靠距离可通过计算基本实体间的最短距离来获得。文献［7］论述了各种基本图元间(如线与线、线段与圆弧、圆弧与圆弧)碰靠距离的计算方法，从而实现零件的平移和靠接操作。研究表明，不规则零件中各实体(尤其是弧等曲线)的碰靠计算复杂度较高，影响排样系统的执行效率。本文采用了一种简单而有效的方法来计算碰靠距离，即对零件图形中各图元外轮廓进行离散化处理，用若干个离散点形成的连续的直线段构建多边形来近似描述零件图形，这样将碰靠运算转化为各离散点与离散点构成的直线段沿碰靠方向的求交和求距的计算，最终取其最小值作为碰靠距离。图元离散化过程简化了图形的表示方法，如直线段只需提取其起始点和终止点;圆弧则因规则性以其起始点和终止点(包含之)来均分得到各离散点;对于复杂曲线则根据其曲率变化适当选择离散点。

假设给定两个零件图形P和Q，碰靠方向为水平方向(其中任意方向都可以通过图形变换将其转化为所需碰靠方向，这样便于描述计算)，其碰靠距离求解算法的主要步骤如下。

(1)离散化图形P和Q，分别产生各自的离散顶点序列:P={p1，p2，…，pn}和 Q={q1，q2，…，qm}。其中各顶点的坐标可表示为(X(pi)，Y(pi))或(X(qj)，Y(qj))。

(2)计算图形P上各顶点到Q的距离。对于点 pi(i=1，2，…，n)，遍历 Q 上所有顶点 qj(j=1，2，…，m)，如果满足条件:Y(qj+1)≤ Y(pi)≤Y(qj)或Y(qj)≤Y(pi)≤Y(qj+1)，则计算pi点沿水平方向的直线与线段qjqj+1的交点并求出pi与交点的距离记为dij;否则计算下一个点pi+1直到完成P上所有顶点的计算。从所得距离中取最小距离值min dij。

(3)同样方法计算图形Q上各顶点到P的距离，得到最小距离min d'ij。

(4)比较min dij和min d'ij，取其最小者为零件P和Q的碰靠距离，将零件Q或P以此值作为移动量进行平移操作，实现两个零件的靠接，如图4所示。

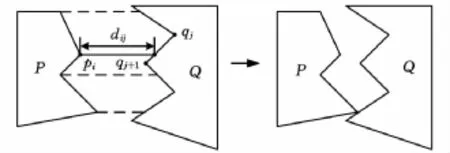
图4 零件的碰靠计算

2 基于最佳吻合碰靠的排样算法

在零件以一定的次序排入过程中，首先在给定的排放区域内通过计算当前零件不同排放角度的静矩，选择最小静矩的入排角度。然后根据设定的碰靠方向，对当前零件进行碰靠操作，为减小计算量，通常以水平和垂直方向作为碰靠方向，使零件尽可能紧密靠接，并以当前排样高度最低作为最佳碰靠定位方案。因此，最佳吻合碰靠过程从某种意义上说是使零件在最小静矩的排放规则基础上再进行碰靠处理从而搜索到排放高度最低的位置。图5给出了零件通过旋转碰靠实现较好的定位排样效果。

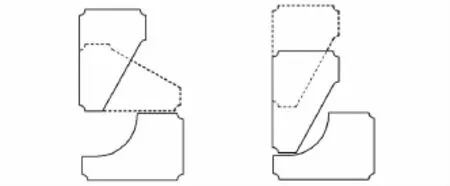
图5 最佳吻合碰靠定位示意

此外对于形状较复杂零件，本文设计的排样系统增加了交互式点对点碰靠方法作为辅助碰靠定位，即依靠人类的先验知识和感官判断，对入排零件可以人为调整选择最佳的碰靠方向使零件沿着规定的靠接定位位置移动，如图6所示。

图6 交互点对点碰靠

无论是自动碰靠还是交互碰靠，评价最佳吻合碰靠定位的目标函数是零件向下向左移动的最大距离或零件实现靠接后的最低排样高度，对于相同排样高度的情况，优先最左靠接位置。目标函数表示为

其中，max(dy)表示高度方向最大碰靠距离，max(dx)表示水平方向最大碰靠距离;α和β为参数因子，α≫β，以保证当前面的函数值不同时，后面的函数值不会对结果的判断造成影响。

碰靠排样算法流程如图7所示，图中虚框中所表示的外循环表示对于排样零件入排次序的优化，优化方法可采用遗传算法、粒子群算法等，可参阅文献［8-9］，本文着重讨论定序情况下的定位碰靠方法，故对其不作详细阐述。

图7 最佳吻合碰靠流程图

3 应用实例

通过对上述算法的描述和分析，本文设计排样系统平台，以剩余矩形法作为解码算法结合自动碰靠算法实现零件定位和排样布局。选择板材长度为8000mm，宽为2000mm。输入两组待排零件，其中以已排零件的面积之和与板长方向的零件包络矩的最高轮廓线以下区域面积S的比率作为材料利用率的评价函数，其目标评价函数表示为

式中，ni为排样零件个体;li为零件包络矩长度;wi为零件包络矩宽度;N为入排零件个数;S为整体排样结构的包络面积。

图8为69个零件的排样图，板材利用率为86.87%;图9为43个零件的排样图，板材利用率为85.63%。

图8 排样布局一

图9 排样布局二

4 结束语

本文在借鉴矩形化策略基础上，将零件以最小静矩(或最低重心)为定位准则选择最佳入排角度进行正交靠接排放和定位，并设计了交互排样中的点对点交互碰靠算法，实现零件以任意碰靠方向进行最优布局调整。碰靠距离的计算采用零件图形离散化处理，实现离散点沿碰靠方向的求交和求距，求解方便简单。利用该算法设计的排样系统在对不规则零件的排样优化中具有较好的稳定性和有效性。

［1］Jakobs S.On Genetic Algorithms for the Packing of Polygons［J］.Eurpean Journal of Operational Research，1996，88:165-181.

［2］Bennell J A，Kathryn A，Dowsland W B.The Irregular Cutting－stock Problem－A New Procedure for Deriving the No－fit Polygon［J］.Computers and Operations Research，2001，28:271-287.

［3］刘嘉敏，佟德刚，黄有群.临界多边形生成算法的改进［J］.沈阳工业大学学报，2005，27(5):567-570.Liu Jiamin，Tong Degang，Huang Youqun.An Improved Approach for No－fit Polygon Creation［J］.Journal of Shenyang University of Technology，2005，27(5):567-570.

［4］Hopper E，Turton B C H.A Genetic Algorithm for 2D Industrial Packing Problem［J］.Computers and Industrial Engineering，1996，37:375-378.

［5］Ismail H S，Hon K K B.The Nesting of Two－dimensional Shapes Using Genetic Algorithms［J］.Proceeding of the Institution of Mechanical Engineers，1995，209(2):115-124.

［6］刘胡瑶，何援军.基于重心NFP的二维不规则形状排样算法［J］.中国机械工程，2007，18(6):723-726.Liu Huyao，He Yuanjun.2D Irregular Nesting Algorithm Based on Gravity Center NFP［J］.China Mechanical Engineering，2007，18(6):723-726.

［7］陈文亮，崔英，李磊.基于自动碰撞技术的最优排样算法［J］.计算机应用研究，2000，17(7):37-39.Chen Wenliang，Cui Ying，Li Lei.The Optimized Nest Algorithm Based on Automatic Touching Technology［J］.Application Research of Computers，2000，17(7):37-39.

［8］梁利东，叶家玮.基于遗传算法的不规则件优化排样的研究［J］.计算机工程与应用，2009，45(2):223-224，228.Liang Lidong，Ye Jiawei.Research of Irregular Parts with Genetic Algorithm［J］.Computer Engineering and Application，2009，45(2):223-224，228.

［9］梁利东，钟相强.基于粒子群优化算法在不规则件排样中的应用［J］.中国机械工程，2010，21(17):2050-2052，2069.Liang Lidong，Zhong Xiangqiang.Application of Particle Swarm Optimization for Solving Irregular Parts Nesting Problem［J］.China Mechanical Engineering，2010，21(17):2050-2052，2069.