允许缺货条件下最优广告与订货策略的联合确定

丁 虹

（合肥师范学院 数学系，安徽 合肥230061）

1 引言

易腐品是指在存储过程中容易发生腐烂、性能衰退和分解的变质类物品，如水果、海鲜、蔬菜、化学药品等。在现实生活中，广告宣传是销售易腐商品时所采用的重要营销手段之一，销售商可通过广告宣传让顾客充分了解销售商品的品质、价格、折扣等一系列信息，从而激发潜在客户购买其销售商品的欲望，进而达到提高商品销售量的目的。但也并非投入广告的强度越大越好，一方面广告投入费用多了，增加的利润不一定能补偿广告投入的费用，另一方面，由于潜在客户毕竟是有限的，当广告投入到一定程度之后，再投入广告，需求也不会有明显的增加了；在考虑广告投入强度问题的同时，销售商还将面临着进货策略问题，若进货少了，会造成广告宣传带来的顾客的流失；而进货多了，将导致资金积压以及库存费用的增大。因此，开展易腐商品广告费用与订货策略的联合确定，对销售商的经营决策具有重要的实际价值。

近些年来，相关的研究文献也不断涌现。文献［1］考虑了广告对需求的影响，并确定了最优广告投入和订货策略。之后文献［2］发展了文献［1］的研究，考虑了品牌广告与地方广告联合作用下的库存模型。文献［3］研究了广告费用与数量折扣联合考虑下的供应链问题，在以上这些文献中，都只考虑到广告费用对于需求的影响，而在现实生活中，正如文献［4］和文献［5］的讨论，需求量与库存水平也是相关的。文献［6］研究了需求既依赖于广告投入费用又依赖于库存水平时，变质率为常数的易腐品在固定订货周期下不允许缺货条件下的库存模型。而在以往的研究文献［4，5，7，8，9］中研究了缺货情况下全部延期和部分延期交货的情况，均发现允许缺货情况下销售商获取了更多的利润。考虑到这个问题，本文在文献［6］的基础上，研究了允许缺货条件下易腐商品广告费用与订货策略的联合确定问题。

2 问题的提出

假定1：零售商所面临的单位时间需求量由三方面所决定，第一方面是固定的需求率D0，第二方面是广告所引起的需求率D1（t），第三方面是由库存所引起的需求量D2（t）。即：

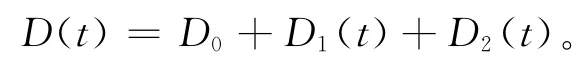
假定2：零售商在单位时间内投入广告费用相同，且设为u（决策变量）。利用文献［6］中的假设，单位时间投入广告费用u时，任意时刻广告所引发的需求率为

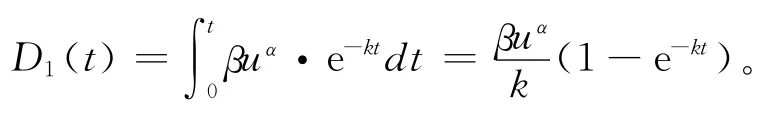
假定3：利用文献［4］中的假设，单位时刻库存水平所引起的需求量D2（t）＝θI（t）（0≤θ≤1）。

假定5：零售商的订货周期为内生变量，设为T。

3 模型1

这个模型讨论允许缺货情况下全部延期交货的情况，这里我们假定单位时间单位物品的缺货成本为c2。当库存量为正的时候，需求量与广告投入费用、库存水平有关，当库存量为负的时候，需求量只与广告投入费用有关。

因此，我们可以得到库存模型：

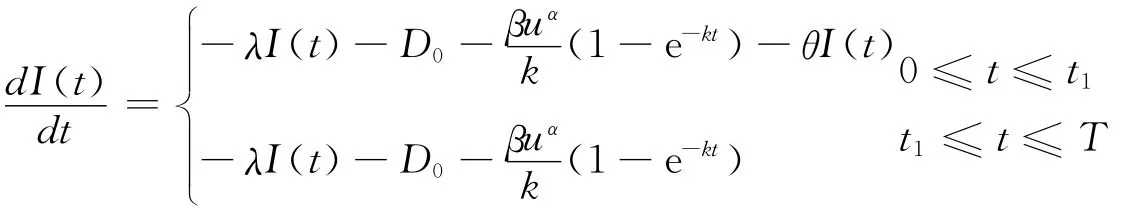
解微分方程得：

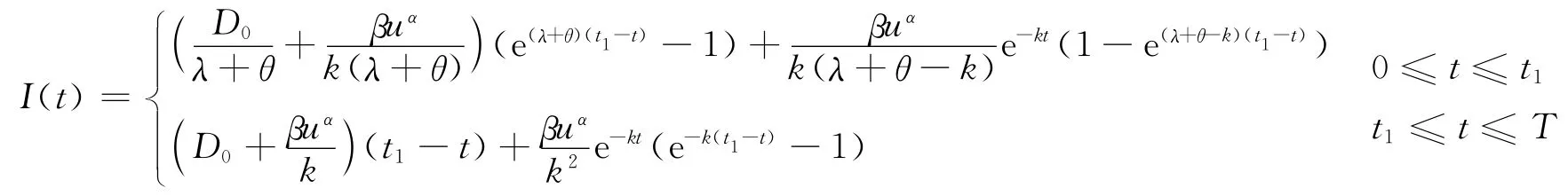
则得到零售商每次订货的订货量：

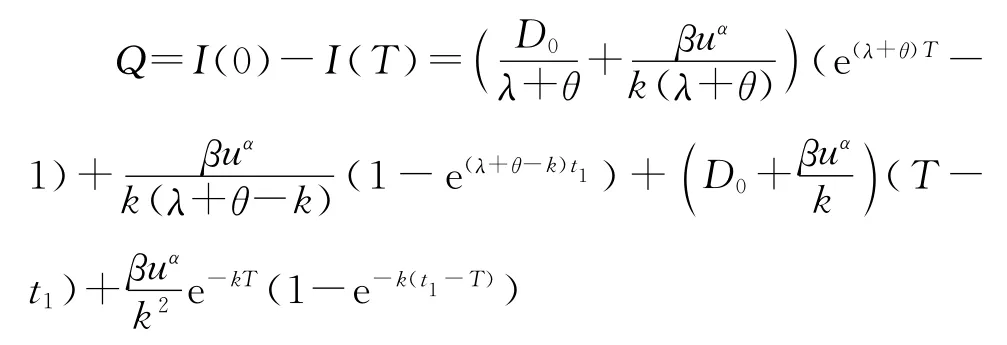
同时，可以得知一个周期内总销售量：

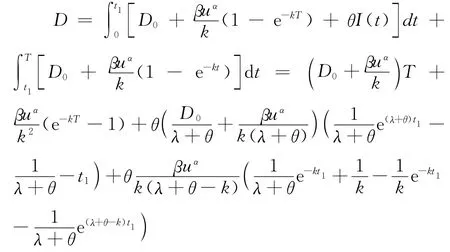
以及一个周期内总库存费用为

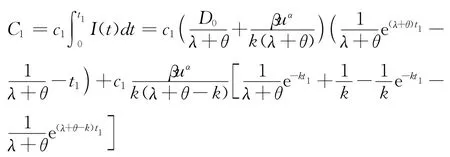
其中：c1为单位时间单位商品的库存费用；

一个周期内总的缺货成本：

其中c2为单位时间单位商品的缺货费用；

此时，可以得到一个周期内零售商的利润函数为：

其中：c为单位商品的进价，p为单位商品的零售价格，A为订购费；

一个周期内利润达到最大的必要条件为

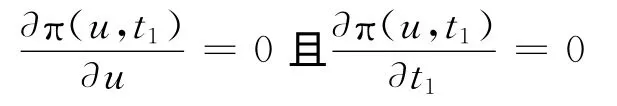
算例分析

为了方便后期算例的比较，我们与文献［6］中的算例的参数赋值保持一致，分别为c＝20元／单位，p＝50元／单位，D0＝15单位／单位每小时，α＝0.2，β＝1.5，A＝300元／次k＝0.5，λ＝0.01，θ＝0.01，c1＝1元／单位时间单位物品，并设c2＝5元／单位物品单位时间，可得最优广告投入费用u＝13.5424元，最优订货量Q＝299.5223单位物品，库存为零的时刻t1＝12.4543，一个周期的最优利润π＝5879.90元。

通过表1，我们可以分析参数λ和θ对广告投入费用、订货量、库存为零时刻与最优利润的影响。在计算的过程中，我们发现，当库存引起需求因子θ过大时，达到最优利润时是不允许缺货的情况（这与实际情况相符），所以在这里我们只需分析θ较小的情况。随着变质率λ的逐渐增加，最优广告投入费用、订货量、库存为零的时刻及一个周期零售商的利润随之减少；随着库存引发需求系数θ的逐渐增加，最优广告投入费用、订货量、库存为零的时刻以及一个周期零售商的利润随之增加。

研究表1，在变质率λ较小的情况下，库存引起需求因子θ对最优广告投入以及最优利润的影响较大，因为在λ＝0.01，θ＝0.04时最优广告投入以及最优利润分别是λ＝0.01，θ＝0.01时的1.379倍和1.288倍，而在λ＝0.04，θ＝0.04时最优广告投入以及最优利润分别是λ＝0.04，θ＝0.01时的1.329倍和1.250倍。而在库存引起需求因子θ较小的情况下，变质率λ对最优广告投入以及最优利润的影响较小，因为θ＝0.01，λ＝0.04时最优广告投入以及最优利润分别是θ＝0.01，λ＝0.01时的0.779倍和0.8227倍，而在θ＝0.04，λ＝0.04时最优广告投入以及最优利润分别是θ＝0.04，λ＝0.01时的0.750倍和0.799倍。

表1 参数λ和θ对广告投入费用、订货量、库存为零时刻与最优利润的影响

4 模型2

这个模型讨论允许缺货，但部分延期交货的情况，这里我们假定单位物品的机会损失成本为c3。在一定条件下，需求等待的数量是依赖于已经等待的数量，也就是说如果太多顾客都在等待，他也许就不会等待。

考虑这种情况，利用文献［8］的假设，我们可以得到库存模型：

解微分方程得：

则得到零售商每次订货的订货量：

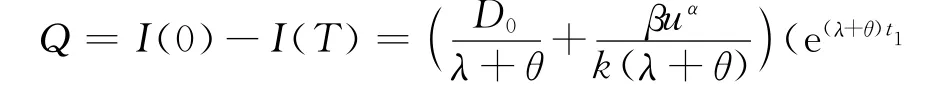
同时，可以得知一个周期内总销售量：

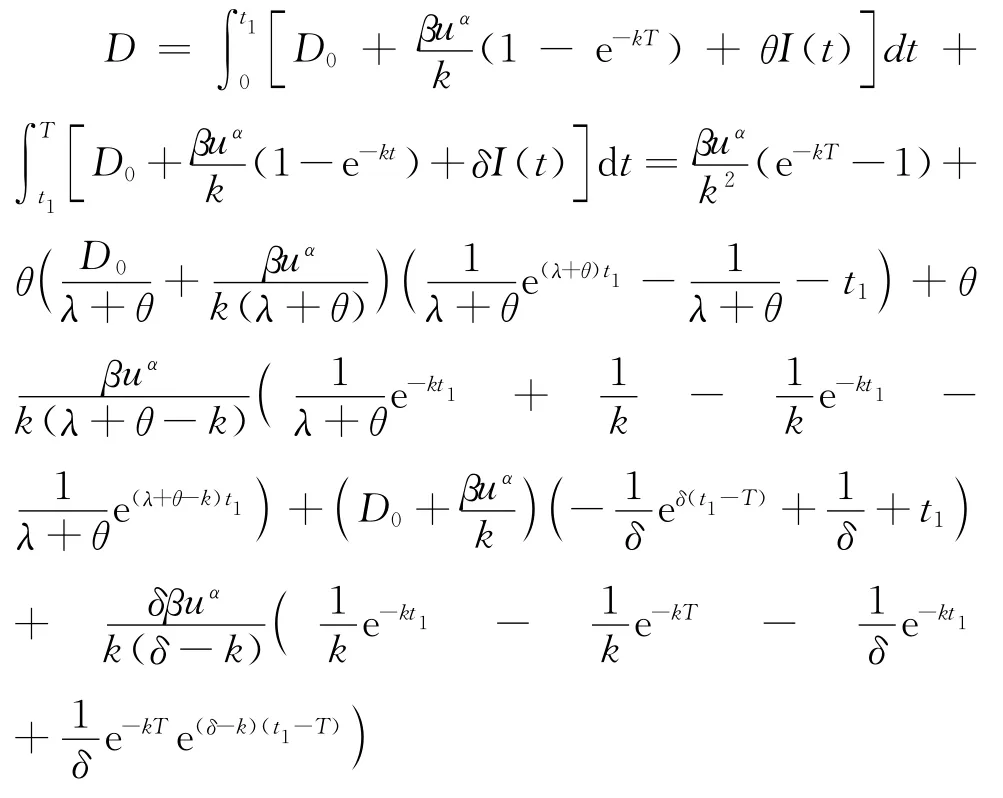
以及一个周期内总库存费用为

一个周期内总的缺货成本：

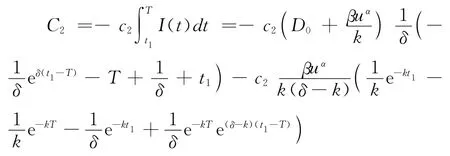
以及一个周期内总的机会损失成本：

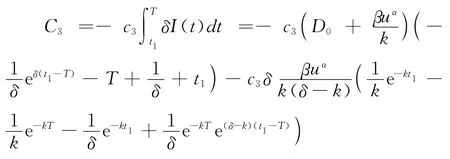
此时，可以得到一个周期内零售商的利润函数为：

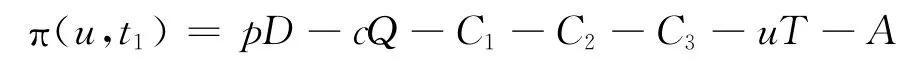
一个周期内利润达到最大的必要条件为

算例分析

为了研究延期交货参数δ对最优广告投入、订货量、库存为零时刻以及最优利润的影响，我们考虑了δ＝0.01，0.02，0.03，0.04；p ＝40，45，50；c2＝4，4.5，5不同情况下的结果，结果见表23。

由表2－3，我们可以发现：（1）随着延期交货参数δ的增加，广告投入费用以及最优利润随之减少；（2）在销售价格较小时，延期交货参数δ对最优广告投入以及最优利润的影响较大；（3）在缺货成本较小时，延期交货参数δ对最优广告投入以及最优利润的影响较大。

表2 延期交货参数δ和销售价格p对广告投入费用、订货量、库存为零时刻与最优利润的影响

表3 延期交货参数δ和缺货成本c2对广告投入费用、订货量、库存为零时刻与最优利润的影响

5 三个模型的比较

本文列出表4用以比较这篇论文以及文献［6］的三个模型。研究表4，我们可以发现：

（1）随着延期交货参数δ的增加，最优广告投入费用以及最优利润逐渐减少；

（2）在延期交货参数δ较小的情况下，δ对最优广告投入与最优利润的影响更明显；

（3）随着延期交货参数δ的增加，允许缺货并部分延期情况下的广告投入费用和最优利润趋向于不允许缺货时的结果。

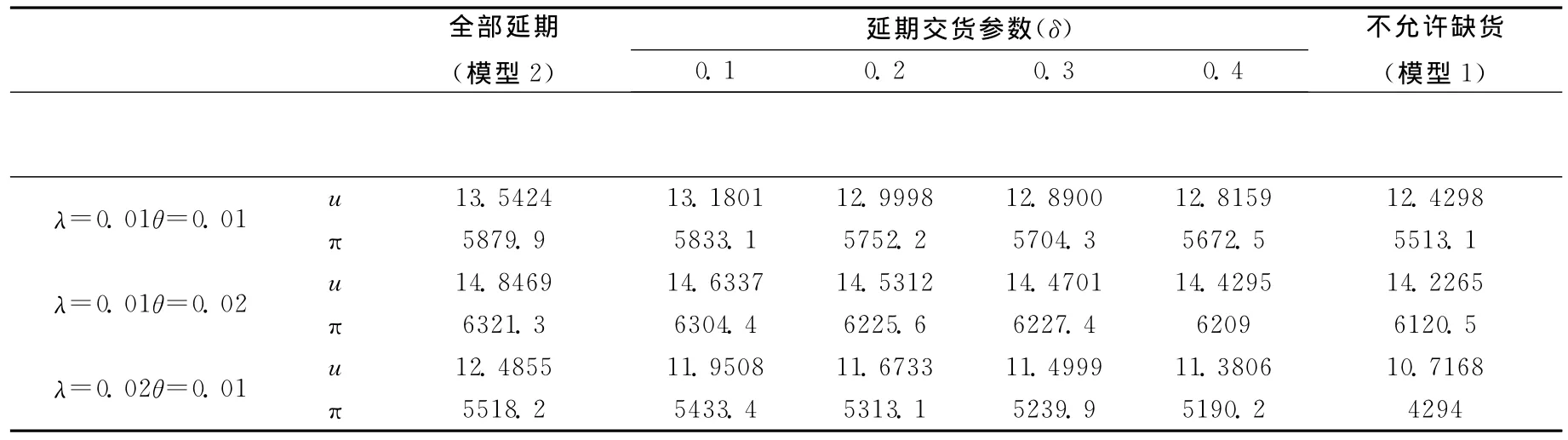
表4 模型1、模型2以及文献［6］中的模型的比较

6 结束语

通过对允许缺货条件下易腐商品广告费用与订货策略进行研究，主要得到以下有意义的结论：

（1）在允许缺货并全部延期交货的情况下，零售商在销售多种商品时，对于变质率较小或变质率由于某些原因变小的物品，我们通过调整货架位置以及摆放方式来提高库存引起需求因子θ，同时忽略变质率较大的物品以便增加总利润。

（2）在允许缺货并部分延期的情况下，当销售价格或缺货成本较小的时候，我们应关注延期交货参数，以便使得利润稳定化。在有条件的情况下，我们可以提高延期交货参数，以使利润较大幅度提高。

（3）与文献［6］不允许缺货相比，允许缺货并全部延期交货情况下零售商投入广告费用将增多，同时所获得的利润也将增大。而对于部分延期的情况，要看延期交货参数δ的大小，当δ足够大的情况下，零售商绝不会允许缺货情况出现，因为利润会降低。而在δ较小的情况下，零售商可以通过允许缺货使自己获得更多的利润同时也说明了研究允许缺货情况下易腐商品广告费用与订货策略的联合确定具有一定的现实意义。

［1］周永务，杨善林.Newsboy型商品最优广告费用与订货策略的联合确定［J］.系统工程理论与实践，2002，22（11）：59－63.

［2］曹细玉，宁宣熙，覃艳华.易逝品供应链中的联合广告投入、订货策略与协调问题研究［J］.系统工程理论与实践，2006（03）：102－106.

［3］曾伟，周永务.考虑最优广告费用及数量折扣的供应链企业间的博弈分析［J］.大学数学，2007，23（5）：115－118.

［4］Padmanabhan G，Vrat P.EOQ models for perishable items under stock dependent selling rate.European Journal of Operational Research，1995，86：281－292.

［5］Dye C Y，Ouyang L Y.An EOQ model for perishable items under stock－dependent selling rate and time－dependent partial backlogging［J］.European Journal of Operational Research，2005，163：776－783.

［6］丁虹.需求依赖于库存和广告下易腐商品订货策略的研究［J］.合肥师范学院学报，2009，27（3）：18－20.

［7］Abad P L.Optimal lot size for a perishable good under conditions of finite production and partial backordering and lost sale［J］.Computers ＆Industrial Engineering，2000，38：457－465.

［8］Sarker B R，Jamal A M.，Wang Shaojun.Supply chain models for perishable products under inflation and permissible delay in payment［J］.Computers ＆Operations Research，2000，27：59－75.

［9］Li Jian，Cheng T C E，Wang S.Analysis of postponement strategy for perishable items by EOQ－based models［J］.Int.J.Production Economics，2007，107：31－38.