地下多相流动数值模拟的GPU并行优化

魏晓辉, 朱 彤, 李洪亮, 李维山, 许天福

(1. 吉林大学 计算机科学与技术学院, 长春 130012; 2. 吉林大学 环境与资源学院, 长春 130012)

随着高性能并行计算技术的快速发展, 将地下多相流动数值模拟与并行计算相结合, 提高地下多相流动数值模拟能力, 已成为解决各种水文地质与环境地质问题的有效工具. 由美国劳伦斯伯克利实验室开发的TOUGHREACT[1]是当前广泛使用的解决地下多相流体运动与地球化学反应运移耦合问题的模拟程序. 但该程序在解决涉及大尺度、 高精度和高复杂性的大规模数值模拟问题时, 应用效果欠佳. 因此, 通过高性能并行计算技术加速TOUGHREACT的数值模拟过程意义重大, 其中一种方法就是利用图形处理器(GPU)通用计算技术实现[2].

目前, 有关地下水流数值模拟的并行化研究主要基于集群系统, 结合MPI技术和现有的并行线性求解软件包(AZTEC, Petsc等)实现. 如: Zhang等[3]利用TOUGH2-MP模拟了位于NevadaYucca山脉非饱和区域的水气运输及热传导; Huang等[4]结合MPI消息传递编程模型及Schwarz类区域分解法实现了MODFLOW与RT3D的并行化; Dong等[5]针对MOLDFLOW中的PCG(preconditioned conjugate gradient)软件包, 基于多核CPU平台, 应用OpenMP并行编程方法, 对修正的不完全Cholesky共轭梯度法(MICCG )进行了部分并行化, 对多项式共轭梯度法(POLCG)进行全部并行化, 实现了MODFLOW在共享存储环境下的并行计算, 在8核心的并行计算机可以获得1.40～5.31倍的加速比; Ji等[6]实现了一种基于CUDA的大规模地下水流模拟求解器, 对模拟过程中使用Jacobi预条件子的共轭梯度法进行并行化, 并在不同的GPU上执行, 相对于CPU串行程序达到了1.8～3.7倍的加速比.

本文通过对TOUGHREACT软件的相关原理与并行性分析, 提出并实现了一种基于CUDA平台的线性方程组并行求解策略, 在保证算法正确性和求解精度的前提下, 相比于串行程序取得了良好的加速效果. 然后将并行程序整合入TOUGHREACT软件包中替代原有的求解器, 实现了基于CPU+GPU异构体系的地下多相流动数值模拟.

1 预备知识

1.1 GPU通用计算

基于GPU通用计算技术(general-purpose computing on graphics processing units, GPGPU)的并行策略与基于OpenMP的方式类似, 也是利用多线程实现对求解过程中费时操作的并行计算, 而且GPU能开辟许多线程进行计算, 更适合完成具有高度并行化的计算密集型任务. 在GPGPU体系结构下, 执行并行程序时会产生CPU与GPU之间的数据通信. 因此, 进行基于GPU的并行程序设计时, 在最大限度挖掘程序并发性的同时, 还要考虑如何控制CPU与GPU之间的通信开销.

CUDA(compute unified device architecture)编程平台以C语言为基础, 编程人员可使用熟悉的C语言调用CUDA中的库函数完成GPU编程. 在CUDA程序架构中, 程序执行区域分为两部分： Host与Device. Host指CPU, 在CPU上执行的代码称为Host代码； Device指GPU, 在GPU上执行的代码称为Kernel代码. CPU控制GPU执行, 调度分配任务, 而大量需要并行计算的工作则由GPU实现. 图1为CUDA程序的Kernel执行与线程组织模型. 由图1可见, 每个block内的所有线程必须存在于同一个处理器核心中, 且共享该核心有限的存储器资源, 因此, 一个block内的线程数是有限的. 在目前的GPU上, 一个block可以包含多达1 024个线程. 实际执行时, 每个block内的线程以32为单位组织成线程束(warp), warp是GPU上处理器资源调度的基本单元, 同一warp内的线程天然同步.

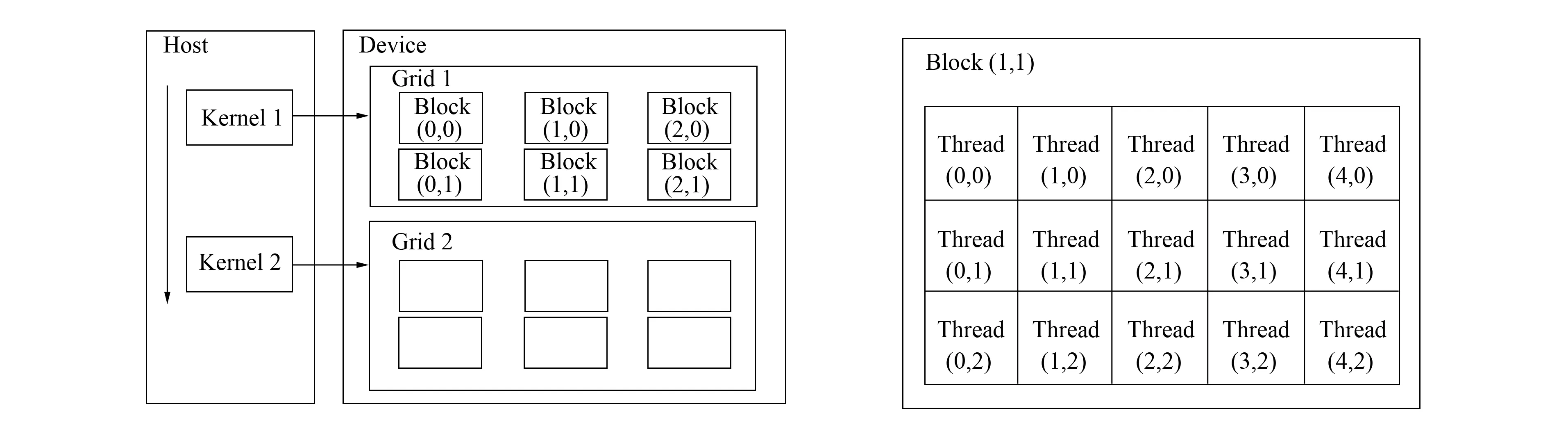
图1 CUDA程序Kernel执行与线程组织模型Fig.1 CUDA program kernels and threads structure

1.2 空间离散及相关求解方法

TOUGHREACT采用积分有限差分法(integral finite difference method, IFDM)[7]将模拟区域离散成任意形状的多面体. 计算过程中, 只需要单元的体积与面积及单元中心到各个面的垂直距离, 使得该方法在处理任意形状的单元时不必考虑总体坐标系统, 同时也不受单元块邻近单元数的限制. 基于多相流具有很强的非线性特征, 程序利用Newton-Raphson迭代法求解非线性方程组, 并在计算过程中, 根据收敛速度调整时间步长. Newton迭代法的求解过程是一种数值逼近的计算方法, 迭代过程中, 每步迭代都要求解一个大型稀疏线性方程组. 共轭梯度类算法是目前的主流算法, 该方法需要的控制参量少, 迭代算法稳定, 不易使解发散, 对不同类型的问题有较强的适应性, 结合预处理技术, 容易形成稳定、 高效的线性方程求解器. TOUGHREACT提供给用户3种预处理共扼梯度法求解稀疏矩阵线性方程组, 分别是双共扼梯度求解、 Lanczos类的双共扼梯度求解和稳定双共扼梯度求解.

2 数值模拟过程并行性分析

2.1 模拟过程分析及并行化

TOUGHREACT经过不断的完善扩充, 源代码十分庞杂, 移植工作量巨大. 因此, 本文采取将一部分热点代码优先向GPU移植的策略. 先对程序结构和执行过程做简要介绍. 程序的数值模拟过程大致可分为两部分： 每一个时间步, 先进行地下多相流体运动的模拟计算并更新相应网格的物理参数, 然后进行地球化学运移计算, 二者的计算过程都涉及到数值方程求解, 但方程的组织形式和规模不同. 地球化学运移过程中所形成的方程组是对每个网格计算单元进行组建, 而地下多相流的方程组是在所有网格计算单元的层次上组建, 在数值计算方法上有差别, 本文主要对地下多相流体运动的数值模拟计算问题在GPU上并行实现.

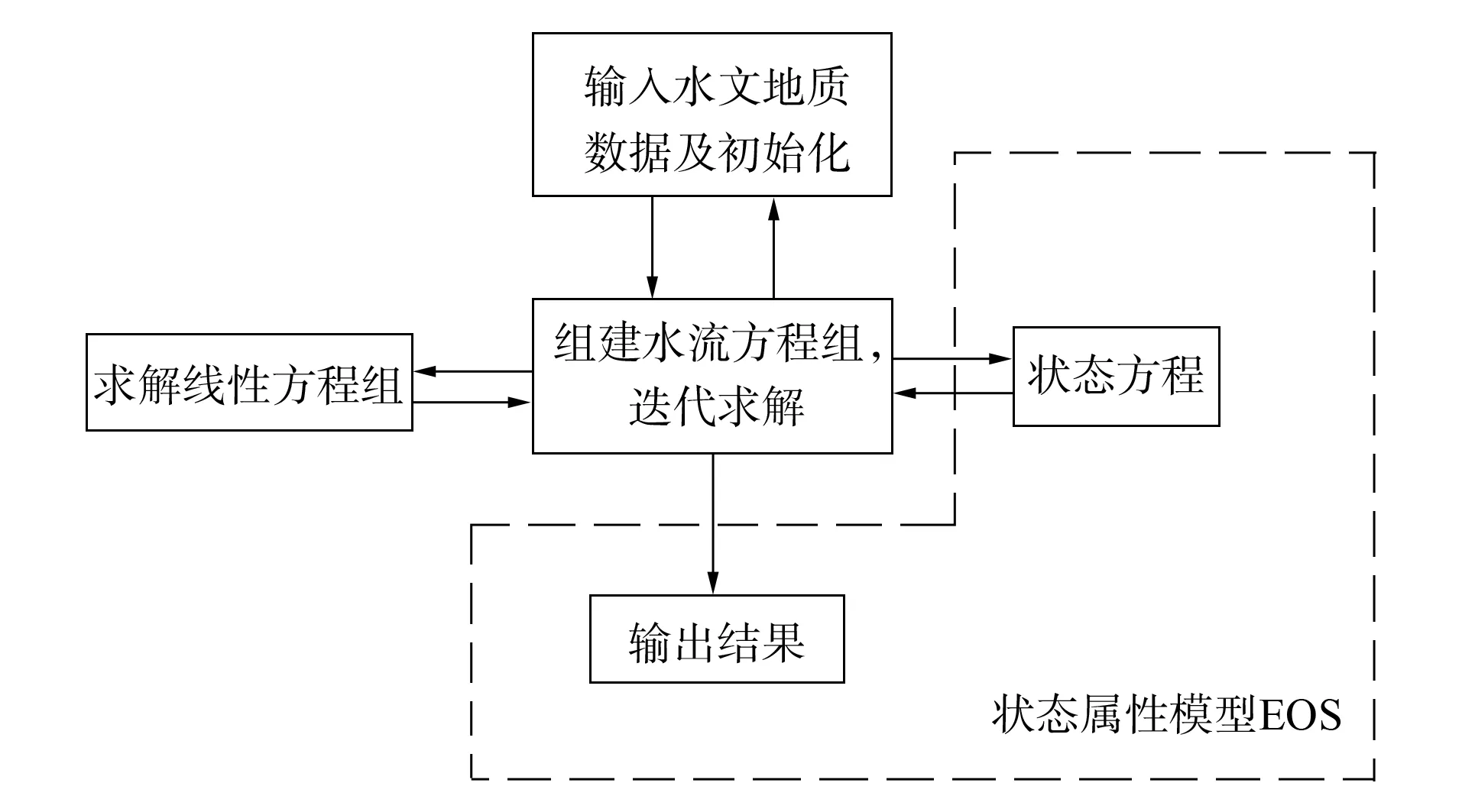
图2 TOUGH2模块化结构Fig.2 TOUGH2 program module structure

TOUGHREACT沿用了TOUGH2[8]中求解多相流问题的相关模块. TOUGH2的程序结构设置为模块化如图2所示, 主要的水流和运移模块可以与不同水流属性模型相互作用, 处理不同的多组分、 多相流系统.

根据文献[9]的分析, 程序的主要计算时间集中在对非线性方程组的Newton迭代过程(80%以上). 在此过程中, 组建线性方程组Ax=b的Jacobian系数矩阵A的时间约占30%, 线性方程组求解时间约占60%. 因此, 本文对其最耗时部分(稀疏线性方程组的求解)进行GPU并行优化. 图3为程序执行流程和基本任务划分模块.

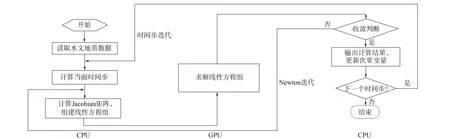
图3 主要模块GPU计算流程Fig.3 Implementation of computing procedure on GPU

2.2 预处理稳定双共轭梯度法并行性分析

为了达到更好的收敛效果, 本文使用预处理稳定双共轭梯度法求解线性方程组时, 先通过不完全LU分解(ILU)[10]对方程组的系数矩阵进行预处理. 目前对稀疏矩阵ILU分解的并行化瓶颈主要在于现有算法的数据依赖性很强, 导致可利用的并行性不足, 不适合在GPU上实现. 本文中的不完全LU分解操作由CPU串行执行.

下面对程序中涉及到求解线性方程组的稳定双共轭梯度法(Bi-conjugate gradient stabilized, BiCGSTAB)[10]进行分析. 算法的描述参见文献[10], 算法从初始解x(0)开始每步迭代都要进行如下操作：

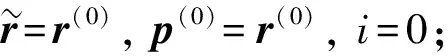
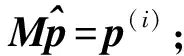
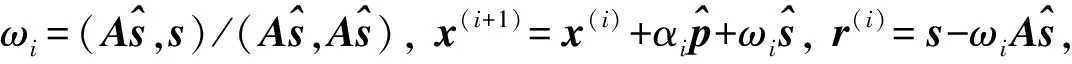
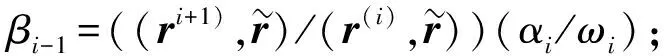
设系数矩阵A为n阶可逆矩阵, 平均每行非零元个数为k,M(M=L×D×U)为通过不完全LU分解得到的预条件子, 其中:L和U分别是m阶上、 下三角矩阵, 平均每行非零元数为s;D为m阶对角矩阵. 每次迭代中各种计算所需次数及复杂度列于表1.

表1 稳定的双共轭梯度法中各计算步的计算复杂度分析

由表1可见, 综合考虑各计算步骤的计算次数和复杂度, 稀疏矩阵与向量的乘积运算(sparsematrix-vectormultiplication,SPMV), 向量内积和三角方程组求解是算法中最耗时部分, 对使用稳定双共轭梯度法求解的计算性能有很大影响.SPMV操作具有行无关的特性, 因此非常适合在GPU上并行实现. 考虑到无论求解上三角方程组, 还是下三角方程组, 在回代过程中, 并行度会越来越小, 从m-1到1逐次递减. 同时对于稀疏矩阵, 非零元素所占比例非常小, 并行度会更小. 因此, 本文在CPU上进行三角方程组的求解, 稀疏矩阵与向量乘积(SPMV)等计算步骤均由GPU执行. 此外, 由于向量內积运算在GPU中运行比SPMV遇到的性能瓶颈少很多, 所以优化工作将集中在SPMV上.

3 稳定双共轭梯度法的GPU并行化

由上述分析可对并行程序中CPU和GPU的计算任务做出划分, 将整个求解过程分成稀疏矩阵向量乘积运算、 向量內积、 向量加减、 向量乘标量和预处理方程组求解等几个步骤. 为了获得较好的整体优化效果, 本文对不同操作采用不同策略.

3.1 稀疏矩阵存储格式

对于线性代数方程组Ax=b, 其系数矩阵A是一个对称正定的大型稀疏矩阵. 选择合理的稀疏矩阵存储格式对迭代求解计算性能的提高有显著作用. 对稀疏矩阵存储格式的定义应包括非零元素的值和非零元素在矩阵中的位置信息. 常用的稀疏矩阵存储格式是行压缩(compressed sparse row, CSR)格式, CSR格式把一个二维矩阵压缩到一维数组中, 对某个稀疏矩阵, 可以把全部非零元素记录在数组Data中, 然后用数组Ptr记录每行上第一个非零元素在数组Data中的索引, 每个非零元素对应的列坐标记录在Indices数组中. 基于CSR格式的SPMV具有高度的并行性, 有利于使用GPU对SPMV进行并行加速. 稀疏矩阵CSR存储格式为

3.2 并行归约求和

并行归约(reduction)是一种可以实现并行求和、 求乘、 求最大(小)值等操作的方法, 用途广泛. 本文使用并行归约的方法对同一block(warp)内线程求得的中间结果进行并行求和. 初始阶段每个线程读入一个数据, 在后续循环中, 每轮使用上一轮循环中一半的线程进行tid与tid+s的求和, 其中s为线程跨度. 以half-warp(16个线程)为例, 有：

1)s=8. 由tid=0,1,2,3,4,5,6,7的线程执行data[tid]+data[tid+8]计算;

2)s=4. 由tid=0,1,2,3的线程执行data[tid]+data[tid+4]计算;

3)s=2. 由tid=0,1的线程执行data[tid]+data[tid+2]计算;

4)s=1. 由tid=0的线程执行data[tid]+data[tid+1]计算, 此时data[0]中保存的即为该half-warp输入的16个数据之和.

图4 规约求和Fig.4 Reduction procedure

由于下一轮循环中的线程要用到上一轮中的计算结果, 所以在每次循环中都要进行一次线程同步操作, reduction的执行过程如图4所示.

3.3 稀疏矩阵向量乘并行化

本文借鉴文献[11]的CSR格式稀疏矩阵与向量乘积在GPU中的实现方法, 利用warp内线程天然同步特性, 由每个warp计算结果向量的一个元素, warp中的每个线程负责计算每个非零元与相应标量的乘积, 计算过程相互独立, 可较大限度利用GPU处理器资源.

基于CSR格式的SPMV的Kernel.

thread_id =blockDim.x×blockIdx.x+threadIdx.x;； //每个线程的编号

warp_id=thread_id/32; //每个线程所在warp的编号

lane=thread_id&(32-1); //每个线程在当前warp中的编号

_shared_vals[128]; //定义共享内存数组;

row=warp_id; //每个warp计算结果向量的一个结果;

If (row

vals [threadIdx.x]=0;

for (jj=ptr [row]+lane;jj

vals[threadIdx.x]+=data[jj]×x[indices [jj]]; //warp内线程同时计算非零元素与相 应标量的乘积, 中间结果存入数组vals中；

for(0≤lane<32);

Reduction; //对同一warp内线程求得的中间结果进行并行归约求和

If (lane==0)y[row]+=vals[threadIdx.x]; //每个warp内的第一个线程保存结果

end.

3.4 向量内积并行化

为了提高内积计算的并行度, 本文使用一种CPU+GPU的混合归约方法, 核心思想是归约操作分两步完成： 第一步将参与运算的向量划分成多个部分, 由每个block计算一对小向量的内积, block中的每个线程负责对应标量的乘积, 计算结果存储在共享内存中, 然后将结果相加得到小向量的内积； 第二步将第一步每个block求得的小向量内积传送到CPU, 由CPU累加后得到最终结果.

由于block个数不能大于512, 为了充分利用GPU上的计算资源, 本文动态分配每个block内的线程数(即每个小向量的长度). 小向量长度m最小为128, 当n>128×512时,m=256； 当n>256×512时,m=512； 当n>512×512时,m=512×((n-1)/(512×512)+1). 这样不同规模的问题都能得到最佳warp块装载量.

Block大小为128的向量内积Kernel.

thread_id=blockDim.x×blockIdx.x+threadIdx.x;； //每个线程的编号

tid=threadIdx.x//每个线程在block中的编号

_shared_res[128]; //定义共享内存数组

res[tid]=v[thread_id]×w[thread_id]; //中间结果存入数组res中；

for (0≤tid<128)

Reduction； //对同一block内线程求得的中间结果进行并行归约求和

if(tid<1)y[blockIdx.x]=res[0]+res[1]; //每个block内的第一个线程保存结果

end.

3.5 向量加减、 向量乘标量和预处理方程组求解

向量加减和向量乘标量计算较简单, 为了减少CPU与GPU间的通信开销, 向量加减和向量乘标量计算也在GPU上完成. 本文借鉴CUDA SDK中的方法实现. 对于求解预处理方程组时遇到的两次三角方程组求解由CPU完成.

4 实验结果

4.1 实验平台

本文实验在PC机上完成, CPU为Intel Core Quad CPU Q8300@ 2.50 GHz, 内存2 GRAM, 显卡芯片型号为Geforce GTX460, 操作系统为32位的CentOS 5.5, 使用Intel Fortran编译器和Nvdia的nvcc编译器对混合代码进行编译, CUDA工具包的版本是3.0.

4.2 实验设计与结果分析

由实际应用产生的稀疏矩阵规模分别为： 150×150, 1 068×1 068, 2 583×2 583, 6 453×6 453.

图5 GPU并行程序各部分执行时间百分数Fig.5 Time proportion of program execution on GPU

实验1为了验证CPU到GPU的数据传输对并行算法执行效率的影响, 本文针对不同规模的数据集进行了测试. 实验结果如图5所示.

由图5可见, 当稀疏矩阵规模为150×150时, 从CPU到GPU的数据传输占据了程序执行的大部分时间, 是影响程序执行速度的主要瓶颈.程序中的数据传输主要发生在初始化阶段, 即将以CSR格式存储的系数矩阵从内存一次性拷贝到GPU显存的过程.

实验2为了验证本文提出的算法对SPMV和向量内积算法的加速效果, 使用CPU(Q8300)和GPU(GTX460)各执行100次操作, 进行性能对比, 结果如图6和图7所示.

图6 矩阵向量乘执行100次耗时Fig.6 Time spent on 100 times SPMV

图7 向量内积操作执行100次耗时Fig.7 Time spent on 100 times inner product

由图6和图7可见, 当矩阵规模只有150×150时, 稀疏矩阵向量乘计算在CPU和GPU上的执行时间基本持平, 而GPU上的向量内积计算比CPU串行执行更耗时. 这是因为当矩阵规模太小时, GPU上同时运行的线程数有限, 导致流处理器大量空置, 相当于串行执行, 且还要考虑其中的同步开销. 而随着矩阵规模的增大, GPU上计算资源占有率提高, 优势逐渐显现. 当矩阵规模达到6 453×6 453时, GPU上执行单次SPMV计算相对CPU的加速比达到3.4倍.

实验3为了验证本文工作对整个地下多相流数值模拟的加速效果, 本文将并行算法整合进TOUGHREACT, 对整体执行时间进行测试, 测试结果列于表2.

表2 CPU/GPU数值模拟执行时间对比

由表2可见, 随着矩阵规模的增大, 求解所需的迭代次数越来越多. 在双精度条件下, CPU程序和GPU程序都能得到较好的收敛效果(矩阵规模为1 068×1 068时因无法得到收敛解所以未列出). 随着迭代次数的增加, GPU程序进行数值模拟节省的绝对执行时间越多, GPU并行程序的执行效果越好.

综上所述, 本文利用CUDA编程模型特殊的通用计算模式, 对TOUGHREACT软件中的大规模稀疏线性方程组求解器进行了并行化改进, 实现了基于GPU求解线性方程组的预处理共轭梯度法. 随着方程组的规模及稀疏矩阵维度的增多, 基于GPU并行算法的单次执行时间比CPU串行算法有1.7～3.4倍的加速比.

[1] XU Tian-fu, Sonnenthal E, Spycher N, et al. TOURGHREACT: A Simulation Program for Non-isothermal Multiphase Reactive Geochemical Transport in Variably Saturated Geologic Media [J]. Computers & Geosciences, 2006, 32(2): 145-165.

[2] WANG Ming-liang, Klie H, Parashar M, et al. Solving Sparse Linear Systems on NVIDIA Tesla GPUs [C]//ICCS’09 Proceedings of the 9th International Conference on Computational Science. Berlin: Springer-Verlag, 2009: 864-873.

[3] ZHANG Ke-ni, WU Yu-shu, Bodvarsson G S. Parallel Computing Simulation of Fluid Flow in the Unsaturated Zone of Yucca Mountain, Nevada [J]. Journal of Contaminant Hydrology, 2003(62/63): 381-399.

[4] Huang J, Christ J A, Goltz M N. An Assembly Model for Simulation of Large-Scale Ground Water Flow and Transport [J]. Ground Water, 2008, 46(6): 882-892.

[5] DONG Yan-hui, LI Guo-min. A Parallel PCG Solver for MODFLOW [J]. Ground Water, 2009, 47(6): 845-850.

[6] JI Xiao-hui, CHENG Tang-pei, WANG Qun. CUDA-Based Solver for Large-Scale Groundwater Flow Simulation [J]. Engineering with Computers, 2012, 28(1): 13-19.

[7] Narasimhan T N, Witherspoon P A. An Integrated Finite Difference Method for Analyzing Fluid Flow in Porous Media [J]. Water Resources Research, 1976, 12(1): 57-64.

[8] Pruess K. TOUGH2: A General-Purpose Numerical Simulator for Multiphase Fluid and Heart Flow [R]. Berkeley: Lawrence Berkely Laboratory, 1991.

[9] ZHANG Ke-ni, WU Yu-shu, Ding C, et al. Parallel Computing Techniques for Large-Scale Reservoir Simulation of Multi-component and Multiphase Fluid Flow [C]//Proceedings of the 2001 SPE Reservoir Simulation Symposium. Houston, Texas: Society of Petroleum Engineers, 2001.

[10] Saad Y. Iterative Methods for Sparse Linear Systems [M]. Philadelphia: SIAM, 2003.

[11] Bell N, Garland M. Efficient Sparse Matrix Vector Multiplication on CUDA [EB]. 2008. http://mgarland.org.fields.papers.nvr-2008-004.pdf.