部分重叠覆盖流形法的覆盖加密方法
苏海东,祁勇峰
(长江科学院材料与结构研究所,武汉 430010)
1 研究背景和思路
数值流形方法[1](以下简称流形法)是留美学者石根华博士提出的一种新型数值计算方法。该方法采用了覆盖的概念和2套相互独立的网格体系。覆盖,或称为数学覆盖,用以定义各个区域的局部函数。两套相互独立的网格体系,即反映数值解精度的数学网格和表示几何边界和材料分区的物理网格,将整个研究区域划分成有限个相互重叠的区域。这些区域被称为物理覆盖,在各个覆盖上独立定义局部覆盖函数,通过联系函数(或称为权函数)加权平均得到整个求解域上的总体函数。2套网格的交集,称为流形元,跟有限元一样,是基本计算单元,但可具有复杂任意的形状。为保证任意形状的流形元的积分精度,流形法多采用单纯形精确积分方式[1-2]。
当前的流形法研究一般采用有限单元网格来构造数学网格[1,3],权函数取为有限单元的形函数。对任一结点,与该结点相连的所有有限单元形成一个数学覆盖,这样,任一原始的有限元网格就是其结点覆盖的重叠部分,或者说,定义于有限元结点上的覆盖在有限单元的区域内完全重叠,作者在文献[4]中将这种类型的流形法称为完全重叠覆盖的流形法。研究表明,在人们实际比较关注的一些结构关键部位,如孔的周边、裂纹尖端附近等,2套网格的不匹配经常会造成计算精度的下降,流形法的计算结果往往达不到常规有限元法的精度水平[5]。
作者在文献[4,6]中提出部分重叠覆盖的流形法,采用以独立覆盖为主的分析方式,便于在各区域用合适的覆盖函数以适应物理场的局部特征,独立覆盖之间仅用较小的重叠区域以保持覆盖的连续性,从而将现有的基于完全重叠覆盖的流形法扩展到一般意义上的流形研究。作为部分重叠覆盖流形法的首次尝试,该文基于矩形覆盖,给出部分重叠的覆盖形式、基本公式及其实现方式,通过单个矩形数学网格各结点之间的强制约束方式,很方便地将完全重叠的覆盖形式及公式转化为部分重叠的覆盖形式及公式。
众所周知,孔周边等局部区域具有不同于一般情况的复杂变形和应力分布。如果采用较大的数学覆盖、用多项式函数去逼近这样复杂的分布,理论上是可行的,但往往需要很高阶数的多项式级数,而且高阶情况下由于方程组的性态不佳,易引入数值误差,因此效果很差。实践表明,在大的覆盖中单纯依靠提高覆盖函数阶次的方法往往会带来计算结果的振荡跳跃。反之,如果采用较小的覆盖而用相对简单的低阶多项式,则可以更好地逼近实际复杂的分布情况[4]。
这些局部较小的覆盖与其周边较大覆盖的连接是需要考虑的问题。文献[4]采用了统一大小的规则矩形覆盖,在这种情况下,为了将局部区域的覆盖变小以提高计算精度,需要将所有的覆盖都变小,或者至少要将其上、下、左、右4个方向的覆盖都变小,从而增加了很多不必要的计算量。因此要完全发挥出部分重叠覆盖流形法的优势,需要解决如何从小覆盖过渡到周围较大覆盖的问题。本文继续文献[4]的工作,基于矩形覆盖提出局部覆盖加密技术,实现大、小覆盖(或称为网格)的协调过渡。
2 有限元网格的局部网格加密
对于完全重叠覆盖流形法而言,实现大、小覆盖(网格)的过渡相对不太方便。
如图1所示的平面计算,通常在大、小网格之间采用三角形或任意形状的四边形进行过渡,这些方式一般需要人工操作,不能完全体现流形法在网格自动布置上的优势,而且过渡的三角形或四边形往往形状不佳,对计算精度有影响。如文献[6]计算裂纹尖端的应力强度因子,采用基于面积坐标的任意四边形数学网格进行大小网格过渡(使用面积坐标是因为单纯形积分公式要求被积函数为多项式)。结果表明,在裂纹周边覆盖取为高阶多项式时,计算值普遍比理论值偏大。

图1 大、小网格的协调过渡(有限元网格)Fig.1 Transition between small meshes and big meshes when using FEM meshes(compatible approach)
另一种是不协调的过渡方式,如图2所示,大、小网格相连边不匹配,需要采用粘接方法,强制密网格边上的自由度符合粗网格边上的位移分布。以上过渡方法均是常规有限元网格的做法。对于裂纹尖端等区域,位移场分布较为复杂,需要划分非常细密的网格(比常规网格的尺寸小1至2个数量级),用上述方式需要进行多层的过渡,操作起来很不方便。

图2 大、小网格的不协调过渡(有限元网格)Fig.2 Transition between small meshes and big meshes when using FEM meshes(incompatible approach)
3 部分重叠覆盖的覆盖加密
针对部分重叠的矩形覆盖,本文提出大小覆盖的协调过渡方法,以下以图3所示的例子进行说明。在图3(a)的独立覆盖5中进行局部覆盖加密,形成图3(b)的形式,图中显示了与原覆盖5相关区域的结点编号。

图3 局部增加完全重叠覆盖Fig.3 Cover refinement via adding totally overlapping covers
相关结点的控制原则是:
(1)与独立覆盖相连的结点由独立覆盖控制(与独立覆盖的自由度相同),比如,结点 1,6,31,36仍分别由独立覆盖 1,3,7,9 控制;结点 2,3,4,5 由独立覆盖2控制,结点7,13,19,25由独立覆盖4控制,结点12,18,24,30 由独立覆盖6 控制,结点32,33,34,35由独立覆盖8控制。
(2)其它内部结点则为通常的完全重叠覆盖,如结点8至结点11,14至17,20至23,26至29均为完全重叠覆盖的结点。
这实际上是一种在独立覆盖中增加完全重叠覆盖的加密方式。
以下讨论这种过渡的协调问题。由于内部完全重叠覆盖的网格是协调的,因此重点关注与独立覆盖相连的局部网格。以图3(b)中与独立覆盖6相连的网格23-17-18-24为例,这种矩形网格内部结点编号见图4(a),其权函数(即有限单元网格的形函数)为式(1)[7],

式中:ξ0= ξiξ,η0= ηiη,(ξi,ηi)为第 i结点的局部坐标,见图4(a)。
如图4(b)所示,保持结点覆盖1和2上的权函数为式(1)不变,将内部结点3和4所在边合成为1个覆盖,其权函数为

容易验证,W3满足:在覆盖3处为1;在其他2个覆盖处为0;3个权函数之和恒为1。因此在此网格内部满足流形覆盖联系函数(权函数)的所有条件,在水平方向上,由结点覆盖1和2过渡到独立覆盖3是协调的。再考察与网格23-17-18-24上、下相连的网格,比如17-11-12-18,两者共用一条边17-18,在上、下方向过渡也是协调的。因而总体上这种过渡方式是完全协调的。

图4 矩形网格Fig.4 A rectangular mesh
实际上,仍采用一般的权函数式(1),用文献[4]所述的强制约束方式,将结点4约束到结点3(即结点4和结点3的自由度相同),就可以很方便地实现式(2)。
以上方式可以根据计算精度的要求在局部提高网格密度,如在图3(b)的基础上进一步加密成图5的形式。
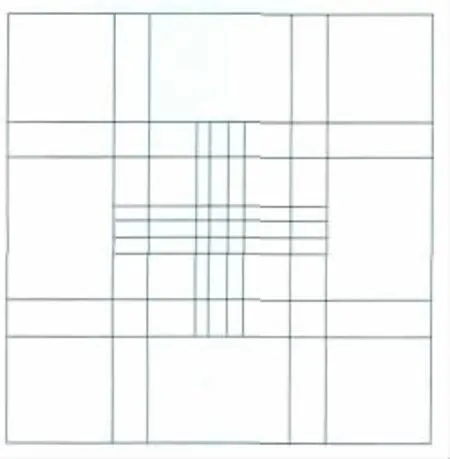
图5 进一步加密覆盖Fig.5 Further refinement
除了上述在局部增加完全重叠覆盖的加密方式外,还可以增加部分重叠的覆盖,如图6所示,在图3(a)的独立覆盖5中增加独立覆盖10至18,原理与上述完全重叠覆盖的情况类似。
进一步推广到采用完全重叠覆盖和部分重叠覆盖相结合的多种形式,所有形式都可以保证协调性,因此这种覆盖加密的方式是非常灵活的。直观上看,这种覆盖加密方式也是很方便的,只要在需要加密的覆盖内增加横线和竖线。采用文献[4]所述的强制约束方式,按照上文所述的控制原则,可以由计算机自动生成结点之间的约束关系。另外,本文虽然仅讨论了二维问题,但其思路同样适合于三维的长方体覆盖情况。
4 算例
以下通过2个算例验证上述方法的有效性。
4.1 算例1——重力坝顶部受集中力作用
仍以文献[4]中的重力坝为例,如图7所示,坝高100 m,坝底长为60 m,坝顶宽度20 m,坝体弹性模量为30 GPa,泊松比为0.167。考虑坝顶的上游点作用F=1 000 kN集中力,关注坝体上游面的应力,特别考察部分重叠覆盖流形法模拟自由表面零应力(理论上,上游面σx和τxy为0)的能力。采用稠密网格的有限元计算结果作为对比,划分1 080个4结点等参元,结点总数为1 183。

图7 重力坝及其有限元网格Fig.7 A gravity dam and its FEM meshes
如图8所示的流形元1和流形元2两种网格。流形元1为未采用局部加密的网格,计算结果见表1(同时列出了采用稠密网格的有限元结果作为对比),可见,在上游顶、底部2个独立覆盖中的上游面应力精度稍差。因此,在流形元2的网格中,局部采用完全重叠覆盖对顶、底部2个独立覆盖进行加密,并取独立覆盖n=4阶,局部加密部分取n=2阶。可见,流形元2与流形元1相比,应力精度有明显改善:σx和τxy总体上更接近于0,大部分点的数值在0.1以下,甚至明显好于稠密网格的有限元计算结果;σy与有限元的结果更接近,大部分点(y=10 m至y=70 m处)与有限元结果相差在0.5%以下,其中y=70 m处,流形元1计算得到的应力数值为27.81,与有限元解30.76相差约 10%,而流形元 2的结果为30.75,与有限元解基本相同。
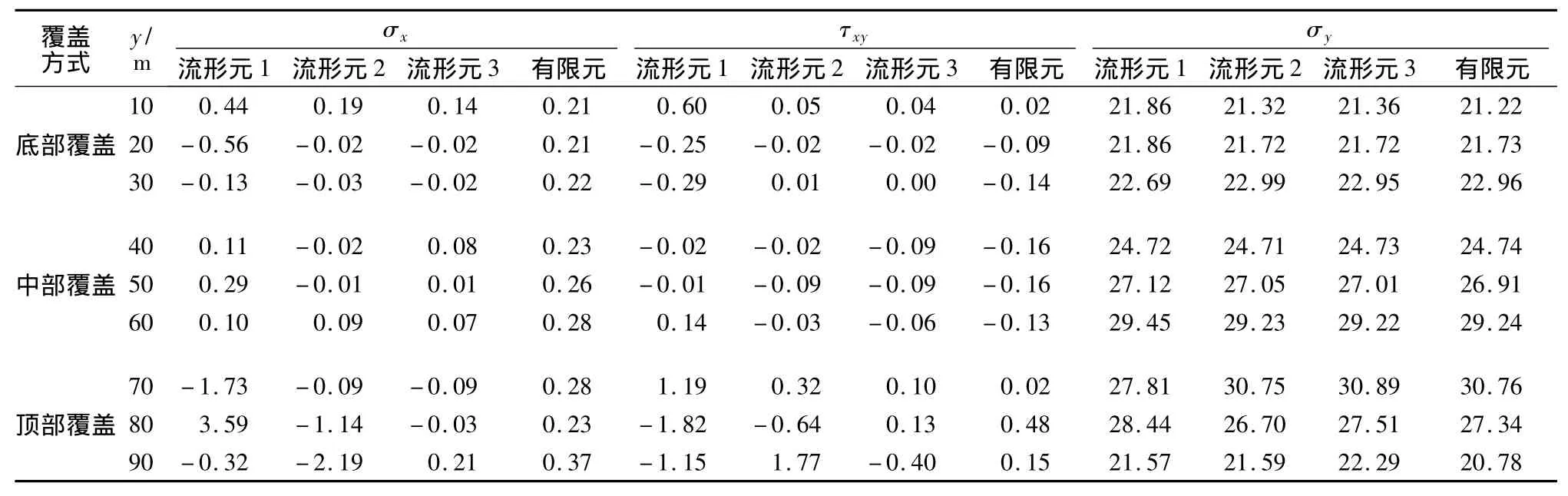
表1 上游表面应力Table 1 Stresses on upstream face of the dam 0.01 MPa
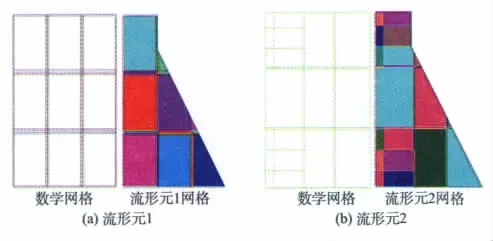
图8 不同流形元计算网格Fig.8 Two NMM meshes
相对而言,高程80,90 m处的精度比其它部位差,说明顶部网格还有进一步加密的必要(单纯提高多项式阶数的效果反而不好)。
进一步在顶部覆盖中采用部分重叠的覆盖加密方式,如图9所示的流形元3的网格,所有的独立覆盖均采用n=4阶,顶部的覆盖由于有集中力的作用,取n=5阶。计算结果见表1。与流形元2的结果相比,计算精度进一步提高。在顶部覆盖处的 σx和τxy更接近于0。
4.2 算例2——圆孔的应力集中
中部开圆孔的矩形板在上、下两端承受均布拉力p,通过计算圆孔左右两侧的垂直向应力与施加的均布拉力之比来求应力集中系数,理论值为3.00,即圆孔处的应力为矩形板两端拉力p的3倍。
考虑了3种网格如图10所示,圆孔周边用完全重叠覆盖的方式加密。
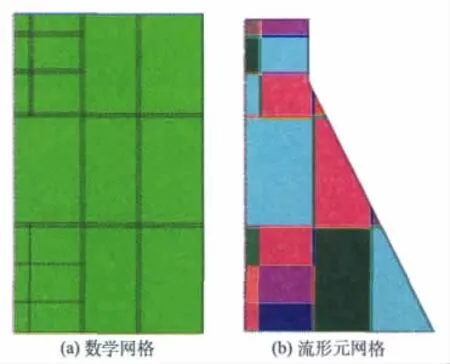
图9 流形元3的网格Fig.9 NMM meshes 3
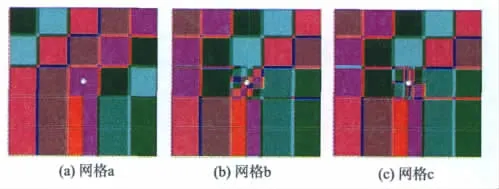
图10 圆孔周边覆盖加密Fig.10 Cover refinement around a circular hole
首先计算没有进行局部覆盖加密的网格a,其中,图中的圆孔底部到结构底部的一条竖线是为了使结构的矩形边界与圆孔之间形成有向环路而设置的[1]。总共有25个独立覆盖,在圆孔所在的独立覆盖中,当多项式阶数n=2时,应力集中系数为1.03;n=4时,应力集中系数为1.09;n=6时,应力集中系数为1.18。可见,应力集中系数随着多项式阶数而增大,但收敛很慢,可以预见,要达到理论值3.00,需要很高的阶数。
再计算网格b,在圆孔所在的独立覆盖中进行覆盖加密。周围的独立覆盖取4阶,计算得到的应力集中系数见表2,表中n表示局部加密的完全重叠覆盖的多项式阶数。可见,计算值虽然接近于理论值,但随阶数n的升高会出现数值振荡,这是在网格密度不够情况下的典型表现。实践表明,在实际物理场分布复杂的区域,单纯提高多项式的阶次往往会带来计算结果的振荡跳跃。
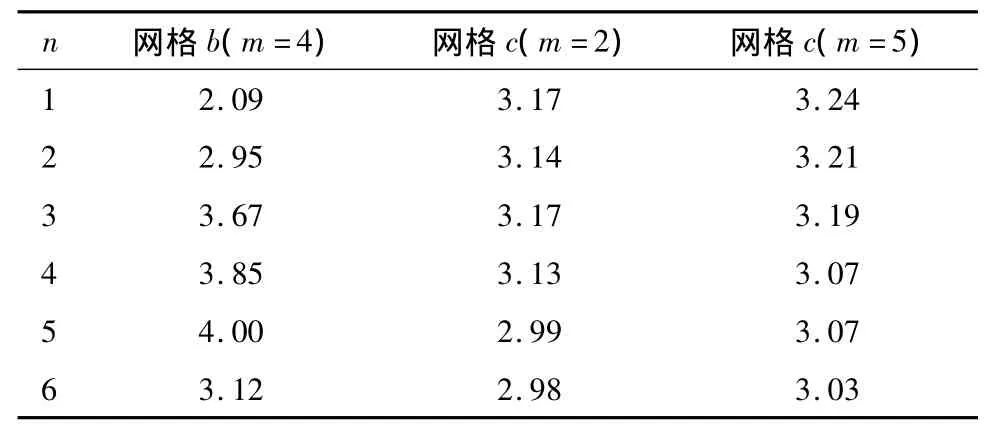
表2 圆孔应力集中系数Table 2 Stress concentration factors of the circular hole
再计算网格c,在圆孔所在的独立覆盖中进一步加密覆盖。周围的独立覆盖取2阶和5阶两种情况,计算结果见表2。可见,计算结果随着局部重叠覆盖阶数的提高而较为稳定地趋向于理论值。
以上算例表明了本文提出的覆盖加密方法的有效性。
5 结语
本文针对部分重叠覆盖的流形法提出了大、小矩形覆盖之间的过渡方式,可以在大覆盖中根据需要加密成为较小的覆盖,并与周边的大覆盖保持协调的联系。此方法相对于以往采用有限元网格的完全重叠覆盖流形法而言,在大小网格的过渡上要方便得多。当然,如何布置加密的覆盖(网格)以及如何安排覆盖函数的阶次使计算达到所需的精度,是需要进一步研究的问题。
部分重叠覆盖流形法的一大优势是便于在局部区域采用特殊的覆盖函数以适应物理场的局部特征。比如,对于裂纹尖端附近区域,其位移往往具有解析的函数形式,采用这种解析函数的特殊覆盖,其收敛性肯定要比通常的多项式逼近快得多[8]。然而,这种特殊覆盖函数的适用区域非常小。因此,在大的覆盖中进行覆盖加密,不仅可以降低每个覆盖中实际函数分布的复杂度,而且还可以提供适用于解析解的特殊覆盖区域。采用本文提出的部分重叠覆盖流形法的局部加密方法,可以很方便地实现周边大覆盖到裂纹尖端局部覆盖的协调过渡,这部分研究成果将另文介绍。
致谢:部分重叠覆盖的流形法思想是由石根华博士提出的,本文的研究工作得到了石根华博士的指导,在此表示衷心的感谢!
[1]石根华.数值流形方法与非连续变形分析[M].裴觉民译.北京:清华大学出版社,1997.(SHI Gen-hua.Numerical Manifold Method(NMM)and Discontinuous Deformation Analysis(DDA)[M].Translated by PEI Jue-min.Beijing:Tsinghua University Press,1997.(in Chinese))
[2]林绍忠.单纯形积分的递推公式[J].长江科学院院报,2005,22(3):32 - 34.(LIN Shao-zhong.Recursive Formula for Simplex Integration[J].Journal of Yangtze River Scientific Research Institute,2005,22(3):32 -34.(in Chinese))
[3]张湘伟,章争荣,吕文阁,等.数值流形方法研究及应用进展[J].力学进展,2010,40(1):1-12.(ZHANG Xiang-wei,ZHANG Zheng-rong,LV Wen-ge,et al.Advances and Perspectives in Numerical Manifold Method and Its Applications[J].Advances in Mechanics,2010,40(1):1 -12.(in Chinese))
[4]祁勇峰,苏海东.部分重叠覆盖的数值流形方法初步研究[J].长江科学院院报,2013,30(1):65 -70.(QI Yong-feng,SU Hai-dong.Preliminary Study of Numerical Manifold Method with Partially Overlapping Covers[J].Journal of Yangtze River Scientific Research Institute,2013,30(1):65 -70.(in Chinese))
[5]苏海东,谢小玲,陈 琴.高阶数值流形方法在结构静力分析中的应用研究[J].长江科学院院报,2005,22(5):74 - 77.(SU Hai-dong,XIE Xiao-ling,CHEN Qin.Application of High-order Numerical Manifold Method in Static Analysis[J].Journal of Yangtze River Scientific Research Institute,2005,22(5):74 - 77.(in Chinese))
[6]祁勇峰,苏海东.部分重叠覆盖的流形法研究报告[R].武汉:长江科学院,2012.(QI Yong-feng,SU Haidong.Research of Numerical Manifold Method with Partially Overlapping Covers[R].Wuhan:Yangtze River Scientific Research Institute,2012.(in Chinese))
[7]王勖成,邵 敏.有限单元法的基本概念和数值方法[M].北京:清华大学出版社,1988.(WANG Xu-cheng,SHAO Min.Basic Principle of the FEM and Numerical Method[M].Beijing:Tsinghua University Press,1988.(in Chinese))
[8]苏海东,祁勇峰,龚亚琦.裂纹尖端解析解与周边数值解联合求解应力强度因子[J].长江科学院院报,2013,30(6):83 - 89.(SU Hai-dong,QI Yong-feng,GONG Ya-qi.Compute Stress Intensity Factors via Combining Analytical Solutions around Crack Tips with Surrounding Numerical Solutions[J].Journal of Yangtze River Scientific Research Institute,2013,30(6):83 -89.(in Chinese))

