新岩滑坡膨胀性软岩Duncan-Chang模型及归一化特性研究

项良俊，王 清，王朝阳，王蕊颖，张 晶，马玉飞，杨俊辉

(1.吉林大学建设工程学院，长春 130026;2.吉林省交通实业集团，长春 130026)

1 工程背景

近年来，吉林至珲春高速公路及其邻域路堑开挖中已经出现多例边坡失稳现象，给工程建设带来较大困难。研究发现，引发滑坡的主要原因是，这一地区分布着膨胀性很强的软岩，岩性为白垩系下统大拉子组(k1d)、上统龙井组(k2l)和第三系珲春组(E2－3h)的粉砂质泥岩或泥质粉砂岩地层［1］。通过总结前人的研究发现［2－4］，对该地区膨胀性软岩基于应力－应变关系的相关研究较少，岩土体的应力－应变关系是岩土体强度和变形特征的基本表现，岩土体强度特征是决定边坡失稳问题的基础，故对该地区膨胀性软岩应力－应变关系的分析研究具有一定的理论和实际工程意义。

由于弹性非线性模型能较好模拟土体非线性变形性质，且结构简单，在有限元分析中得到了广泛应用，Duncan-Chang双曲线模型作为土体弹性非线性模型的代表，得到了最为广泛的应用。徐舜华等研究成果表明土的应力－应变关系存在归一化性状，归一化性状是由归一化应力来体现的［5］。Ladd和Foott［6］根据试验结果认为，大多数饱和黏性土三轴试验的应力－应变关系曲线可以用围压σ3或平均固结压力进行归一化;随后，曾国熙［7］(1980)、李作勤［8］(1987)、徐舜华［5］(2005)、张勇［9］(2006)等国内外学者通过采用不同归一化因子，验证了应力－应变关系存在归一化性状。

本文通过室内三轴固结不排水剪切试验，研究汪延高速公路新岩滑坡膨胀性软岩应力－应变关系，并对土体本构关系进行了研究，获得了Duncan-Chang模型参数，在此基础上研究了膨胀性软岩的归一化性状，为以后的有限元分析和变形预测研究提供参考。

2 土样物质组成及其物理力学性质

土样取于新岩滑坡处，取样点位于近地表处，土呈灰黄色，夹灰色泥岩，粉粒含量较多，土密实且较坚硬，含水率较低。对土样进行X－射线衍射分析和扫描电子显微镜观测，试样中黏土矿物含量很高，高达67%，且黏土矿物中主要以伊/蒙混层矿物和蒙脱石矿物为主，伊/蒙混层矿物相对含量为88%。经颗分试验确定为亚黏土，颗分试验结果见表1。按现行《土工试验方法标准》规定的方法，对土样进行了系列物理性质实验，其结果见表2。

根据实验结果可知，土体具有较强的亲水性和膨胀性，土样具有高塑性，在外力作用下容易发生变形。为了获取土样的强度和变形特征，根据工程施工和运行的实际情况选择不同排水条件对土样进行了固结不排水剪切试验。

表1 土样颗粒各粒径百分含量Table 1 The percentages of soil sample particles %

表2 土样的基本物理性质Table 2 Basic physical properties of soil sample

3 三轴试验研究

本次实验采用固结不排水剪，实验仪器为南京土壤仪器工程公司生产的TSZ3.0－2.0台式三轴仪。实验土样采取真空抽气饱和方法，饱和度可达到95%。试样直径 d=3.91 cm，高 h=8.0 cm，实验过程采用应变控制，试验剪切速率为0.003 2(mm/min)，侧向压力 σ3=100，200，300 kPa。

根据实验结果得到土样主应力差－应变关系曲线，如图1所示。试验表明:主应力差(σ1－σ3)随应变ε1的增大而增大;在低围压下，土样在较小的轴向应变下达到峰值，达到峰值后，主应力差随着轴向应变的增大增长很缓慢，硬化现象不明显;在高围压下，土样主应力差随着轴向应变的增大增长明显，硬化明显。

图1 试样固结不排水剪应力－应变曲线Fig.1 Stress-strain curves of consolidated undrained shear test

上述这些现象是由土样颗粒之间的胶结作用及孔压的消散程度的不同引起的有效应力的不同变化形成的。在低围压下，围压主要是引起了孔隙体积的压缩，颗粒之间结构联结没有太大改变，因而抗剪强度较低，应变硬化现象不明显，从图1上可以看出低围压下曲线出现了一平缓段，即应力平台，对应应力为屈服应力，出现应力平台是因为在剪切过程中，天然结构强度的损失刚好抵消了由于结构变密而引成结合水连结增加的强度;高围压下曲线斜率越来越小，随着变形的增加，抗剪强度基本上是逐渐增强的，这是因为在高围压条件下，围压不仅引起了孔隙体积的压缩，而且还引起了土体微观结构的改变，土的结构性受到破坏，颗粒排列更加紧凑和密实，使得土体抵抗外部变形的能力大大提高，抗剪强度也随之增强，土体结构状态逐渐向重塑土的性状逼近，应力－应变关系曲线呈逐渐硬化型。

4 Duncan-Chang模型参数

4.1 模型简介

1963 年，Kondne 和 Zelasko［11］根据大量土的三轴应力－应变关系试验资料，提出用双曲线拟合土体主应力差与轴向应变关系曲线和轴向应变与侧向应变关系曲线，即在小主应力σ3不变时:

Duncan等人假设轴向应变与侧向应变之间也是双曲线的关系，推导出切线弹性模量Et和切线泊松比νt的表达式，就可以按照增量广义虎克定律进行应力－应变的分析和计算。

式中:Ei为初始切线模量;Pa为大气压力;c，φ为抗剪强度参数;σ1为最大主应力;σ3为围压;Rf，c，φ，K，n，G，F，D 为模型参数。其中，(σ1－ σ3)f为破坏时的偏应力;(σ1－σ3)ult为偏应力渐近值。

本次实验主要为得到Et指标，由式(2)、(5)可知即主要得到 Rf，K，n，c，φ。

4.2 参数计算

(1)根据 ε1/(σ1－ σ3)=a+bε1关系式，绘制ε1/(σ1－σ3)与 ε1曲线，见图2。由该直线确定 a，b，根据a，b即可求得该级σ3作用下的初始切线模量Ei=1/a，偏应力渐近值(σ1－σ3)ult=1/b，具体结果见表3。

图2 试样ε1/(σ1－σ3)与ε1关系曲线Fig.2 Curves of ε1/(σ1 －σ3)vs.ε1

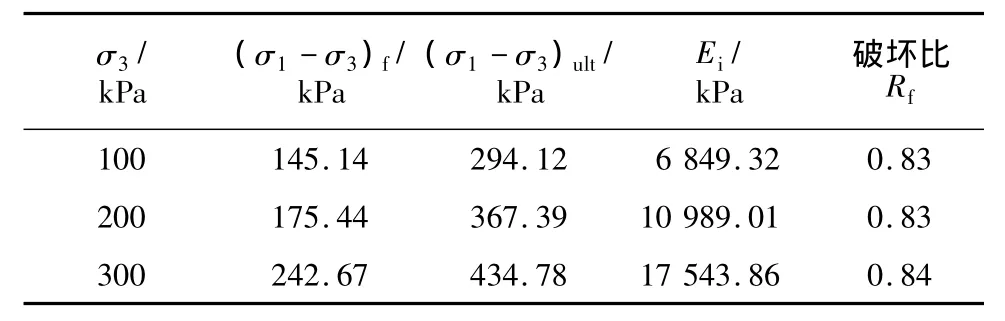
表3 土样的Ei和Rf值Table 3 Values of Eiand Rfof soil sample

(2)根据Ei=KPa(σ3/Pa)n关系式，绘制lg(Ei/Pa)和 lg(σ3/Pa)的关系，如图3所示。由该线的截距及斜率可确定出参数K，n。

(3)根据试样破坏应力值绘出不同周围压力下的摩尔应力圆及摩尔强度包络线，见图4，求出抗剪强度参数c，φ。

图3 试样lg(Ei/Pa)与lg(σ3/Pa)关系曲线Fig.3 Curve of lg(Ei/Pa)vs.lg(σ3/Pa)

图4 试样三轴剪切摩尔强度包络线Fig.4 Triaxial shear strength envelope of Mohr-Conlomb

综上得到模型参数见表4所示。

表4 土样Duncan-Chang模型参数Table 4 The parameters of Duncan-Chang model

5 应力－应变归一化性状研究

5.1 归一化性状

应力－应变关系归一化是指可以用某个归一化因子将不同固结压力下的应力－应变关系归一在一条曲线上，其主要目的在于根据归一化曲线，估计相同条件下任意固结压力时土的力学特性，系统评价应力历史对土体强度变形的影响，并为建立不同种类土体力学特性之间的关系奠定基础。归一化理论基础都是根据Kondner提出的双曲线方程，归一化曲线可统一表示为 Xε1/(σ1－ σ3)～ ε1［10］，X 为归一化因子，采用的归一化因子主要有围压σ3、平均固结压力 σm，(σ3)n(n为 Duncan-Chang模型参数)、主应力差渐近值(σ1－σ3)ult，利用这4种归一化因子分别进行归一化，结果见图5至图8。

图5 围压σ3为归一化因子的归一化曲线Fig.5 Normalized stress-strain curves with σ3 as the normalized factor

图6 围压σm为归一化因子的归一化曲线Fig.6 Normalized stress-strain curves with σm as the normalized factor

由以上归一化结果可知，新岩膨胀性软岩应力应变关系存在归一化性状，归一化效果与归一化因子密切相关。图5、图6表明利用围压σ3以及平均固结压力σm做为归一化因子，在围压为200，300 kPa时，归一化直线相差不大，在围压为100 kPa时，相差较大，说明归一化后的偏应力与剪应变关系与固结压力有关。从图7、图8可看出归一化程度按归一化因子(σ3)n、主应力差渐近值(σ1－ σ3)ult递增，归一化因子X=(σ1－σ3)ult时，归一化程度最好。

图7 (σ3)n为归一化因子的归一化曲线Fig.7 Normalized stress-strain curves with(σ3)n as the normalized factor

图8 (σ1－σ3)ult为归一化因子的归一化曲线Fig.8 Normalized stress-strain curves with(σ1－σ3)ultas the normalized factor

5.2 归一化方程建立以及应力－应变关系预测

本文利用主应力差渐近值(σ1－σ3)ult进行归一化时，由图8可得到归一化方程:

根据表3可得到(σ1－σ3)ult与σ3之间存在着线性关系，对两者进行线性拟合，相关系数R2=0.97，得到两者之间的关系:

将式(7)代入式(6)得到最后的归一化方程:

式(8)即为以(σ1－σ3)ult作为归一化因子建立的应力－应变归一化方程，根据该方程可以预测在不同固结压力下，应力与应变之间关系，为了验证归一化方程，可以基于实验原始数据与预测曲线进行对比，如图9所示，由图可以看出预测曲线能够较好的描述土样应力－应变关系，拟合质量较好，故可以采用归一化方程对新岩滑坡膨胀性软岩在固结不排水剪切作用下，预测其在外力作用下变形规律。

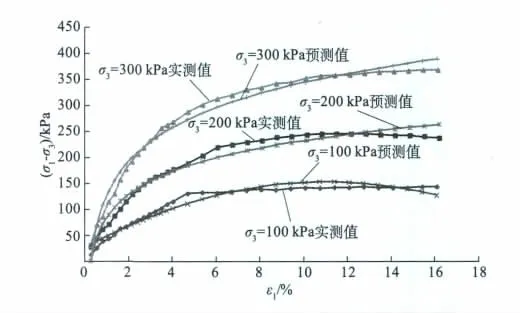
图9 (σ1－σ3)ult为归一化因子的应力－应变关系的预测曲线Fig.9 Predicted stress-strain curves with(σ1－σ3)ultas the normalized factor

6 结论

(1)新岩膨胀性软岩应力－应变关系研究较少，经过实验发现土样在低围压下表现为弱应变硬化型，高围压下表现为应变硬化型，可以用双曲线进行模拟。

(2)采用室内三轴试验，根据三轴主应力差与应变关系曲线、初始切线模量Ei与σ3关系曲线、三轴剪切摩尔强度曲线得到Duncan-Chang非线性模型有限元计算与切线弹性模量Et相关的5个参数，为以后有限元分析研究提供相关资料。

(3)在Duncan-Chang模型基础上，按常用4种归一化因子(围压 σ3、平均固结压力 σm、(σ3)n、主应力差渐近值(σ1－σ3)ult进行归一化时，归一化因子为(σ3)n和(σ1－σ3)ult时，归一化程度较好，且后者归一化程度最好，并且得出在固结不排水条件下应力－应变关系的归一化方程。该方程可以对新岩滑坡膨胀性软岩在固结不排水剪切作用下应力－应变关系进行很好的预测。

［1］何满潮，刘成禹，武雄.延吉盆地强膨胀性软岩边坡加固对策研究［J］.吉林大学学报:地球科学版，2005，35(4):496 －500.(HE Man-chao，LIU Cheng-yu，WU Xiong.A Case Study on the Reinforcement Countermeasures for Strongly Swelling Soft Rock Slope in Yanji Basin［J］.Journal of Jilin University Earth Science Edition，2005，35(4):496 －500.(in Chinese))

［2］何满潮，冷曦晨，衡朝阳，等.延边地区公路沿线膨胀性软岩的发现与试验研究［J］.岩石力学与工程学报，2003，22(7):1151 －1155.(HE Man-chao，LENG Xichen，HENG Chao-yang，et al.Research on Expansive Soft Rock in Yanbian Region［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22(7):1151－1155.(in Chinese))

［3］谷宪明，王 清，冯志仁，等.延边地区公路沿线边坡失稳试验分析［J］.自然灾害学报，2005，14(6):152－157.(GU Xian-ming，WANG Qing，FENG Zhi-ren，et al.Test Analysis on Instability of Slope along Highway in Yanji Area［J］.Journal of Natural Disasters，2005，14(6):152 －157.(in Chinese))

［4］王晓蕾.延吉盘地强膨胀软岩强度特性及本构关系研究［D］.北京:中国地质大学，2011.(WANG Xiao-lei.Research on Strength Characteristics and Constitutive Relationship of Strongly Expansive Soft Rock in Yanji Basin［D］.Beijing:China University of Geosciences，2011.(in Chinese))

［5］徐舜华，徐光黎，程 瑶.黏性土的应力一应变关系归一化性状探讨［J］.地质科技情报，2005，7(24)，170 －174.(XU Shun-hua，XU Guang-li，CHENG Yao.Normalization Character of Stress Strain Relations for Clays［J］.Geological Science and Technology Information.2005，7(24)，170 －174.(in Chinese))

［6］LADD C C，FOOTT R，JSHIHARA K，et al.Stress Deformation and Strength Characteristics［C］∥Proceedings of the 9th International Conference on Soil Mechanics and Foundation Engineering，Tokyo，July 10－15，1977:421－440.

［7］曾国熙.正常固结黏土不排水剪切的归一化性状［C］∥软土地基处理学术讨论会论文选集.北京:水利出版社，1980:13 －26.(ZENG Guo-xi.Normalized Property of Normal Consolidation Clay under Undrained Shear Condition［C］//Proceedings of Academic Convocation about Soft Ground Treatment.Beijing:China Water Conservancy Press，1980:13 －26.(in Chinese))

［8］李作勤.黏土归一化性状的分析［J］.岩土工程学报，1987，9(5):67 －75.(LI Zhuo-qin.Analysis of the Normalized Property of Cohesive Clay［J］.Chinese Journal of Geotechnical Engineering，1987，9(5):67 －75.(in Chinese))

［9］张 勇，孔令伟，孟庆山，等.武汉软土固结不排水应力－应变归一化特性分析［J］.岩土力学，2006，27(9):1509 － 1513.(ZHANG Yong，KONG Ling-wei，MENG Qing-shan，et al.Normalized Stress-Strain Behavior of Wuhan Soft Clay［J］.Rock and Soil Mechanics，2006，27(9):1509 －1513.(in Chinese))

［10］杨爱武，杜东菊，周 金，等.天津吹填软土应力应变归一化特性研究［J］.工程地质学报，2010，18(增1):17 －21.(YANG Ai-wu，DU Dong-ju，ZHOU Jin，et al.Normalized Stress-strain Behavior of Tianjin Soft Dredger Soil［J］Journal of Engineering Geology，2010，18(Sup.1):17 －21.(in Chinese))