短期降雨预报失误对安康水库防洪预报调度的影响

贾志峰，付恒阳，王建莹，刘 招

(长安大学a.环境科学与工程学院;b.水与发展研究院，西安 710054)

汛期水库优化调度是缓解水资源供需矛盾、防洪减灾的直接有效的非工程措施［1］，随着降雨预报精度的提高，降雨信息日益受到重视并被应用于水库调度研究中［2－4］。一旦考虑降雨预报信息，降雨预报失误对水库调度将产生一定的影响，并可能造成风险［5］，因此研究降雨预报失误对水库优化调度的影响十分必要。本文以安康水库为例，基于短期(24 h)降雨预报信息，计算风险发生寄予各个量级降雨预报失误造成的概率，分析降雨预报失误对安康水库优化调度的影响，为安康水库利用不同量级降雨预报信息实施防洪调度提供理论依据。

1 安康水库现状分析

1.1 安康水库概况

安康水库位于汉江上游，是一座以发电为主，兼顾防洪、航运等综合利用的大型水利枢纽。控制流域集水面积35 700 km2。安康水库大坝按千年一遇设计，万年一遇校核。千年一遇洪峰流量为36 700 m3/s，万年一遇洪峰流量为45 000 m3/s。襄渝铁路的防洪标准为百年一遇洪水，在百年一遇洪水标准情况下水库水位不得超过330 m;下游安康市防洪标准为20年一遇洪水，若发生5年一遇洪水，水库控泄12 000 m3/s，发生20年一遇洪水下泄不能超过17 000 m3/s。

1.2 安康水调自动化系统现状

安康水库水调自动化系统主要功能包括:数据实时采集及处理功能;卫星云图接受、显示、处理功能;测报设备监测功能;语音查询及报警系统;水文预报功能等。经测试，系统的数据传输畅通率大于或等于95%，满足大于92%的实用化要求;洪水预报的准确率大于90%;系统水文预报和调度方案分析计算，平均反应时间为5 min 10 s，制作一场洪水预报平均为3 min，系统反应速度满足少于10 min的实用化要求。水库产流预报方案的预报合格率已达到甲级水平［6］。

1.3 流域降雨预报精度分析

为客观反映气象部门近些年的降雨预报理论与技术发展水平，并与安康水库汛期水位动态控制实施期一致。根据安康及汉中气象局历年对汉江上游流域24 h预报成果中，选用2004和2005两年7—10月份及2010和2011年两年7—8月份发布的282 d预报信息。结合安康水库流域实际降雨特征，考虑到预报中雨及以上样本资料较少，将未来24 h降雨预报划分为Ⅰ、Ⅱ、Ⅲ3个量级，分别为:预报无雨(预报值小于0.1 mm)、预报小雨(预报值在0.1～10 mm之间)、预报中雨及以上(预报值大于10 mm)。利用统计学的方法进行“三率”分析，即计算预报的准确率、漏报率、空报率等指标［4］，其中准确率η=(n/m)×100%，漏报率γ=(u/m)×100%，空报率k=［1－(γ+η)］×100%。m为发布某一量级降雨预报次数，n为实际值落于预报等级区域内的次数，u为发布预报中实际降雨量大于预报等级中值域上限的次数。

分析结果见表1:未来24 h降雨预报为Ⅰ量级的准确率为77.1%，漏报率为22.9%，主要漏报为Ⅱ量级;降雨预报为Ⅱ量级的准确率为78.8%，漏报率为15%，空报率为6.2%;降雨预报为Ⅲ量级的准确率为43.1%，空报率为56.9%，空报率较高，即预报偏大，从防洪安全角度上讲，汛期预报偏大是可以接受的。对于Ⅰ量级和Ⅱ量级的预报准确性较高，预报信息可用，但同样存在预报失误，基于Ⅰ量级和Ⅱ量级的降雨预报信息的防洪调度同样存在风险，计算风险发生寄予各量级降雨预报失误造成的概率为本文的核心问题。

1.4 实际降雨量分布规律

采用频率分析法分析不同量级降雨预报条件下实际降雨量分布规律，实际降雨发生频率属于偏态性分布，服从P－Ⅲ型分布［7］，采用矩法估计其平均值和变差系数Cv，由于样本容量较小，用适线法确定偏态系数Cs值，分布参数取值及相应的概率密度参数见表2。

2 贝叶斯定理及事件分析

为计算风险发生后寄予不同量级降雨预报失误造成的概率，首先定义风险发生点，即为降雨预报下，发生了设计洪水对应降雨量。该降雨量超过了对应的预报量级，致使防洪预报调度风险发生。基于降雨预报信息的防洪调度风险发生事件是以不同量级降雨预报事件为条件的，而不同量级降雨预报事件是互斥的，针对条件概率事件，引入贝叶斯定理如下［8－9］:

贝叶斯定理是要采取的行动取决于某种客观、未知自然状态，对于决策者而言是不可控的，但通过判断与采样有可能获得有关自然状态的信息。初始的信息称先验信息，在采样的基础上获得新信息，以此对先验信息修正使决策所依据的信息更近于实际。

假定事件 ei和 Ej，ei(i=1，2，…，n)为互斥事件，Ej(j=1，2，…，m)为运行过程中的某一个事件，样本空间I=e1+e2+…+en，每个事件ei发生的概率为P(ei)，称为先验概率，ei发生时Ej发生的概率为P(Ej/ei)，称为条件概率，则Ej发生时寄予ei的概率为P(ei/Ej)，称为后验概率，则有:

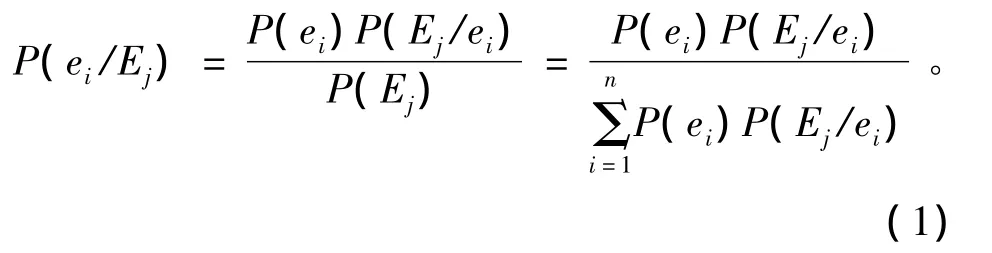
针对基于降雨预报信息的防洪调度风险发生事件而言，ei为不同量级降雨预报事件，充分大样本可统计不同量级降雨预报准确率为P(ei);Ej为发生各个量级设计洪水对应的暴雨量事件，为各级降雨预报条件下的随机事件，则不同量级降雨预报下发生设计洪水暴雨量事件的概率为P(Ej/ei)，发生设计洪水暴雨量寄予不同量级预报失误事件的概率为P(ei/Ej)。

3 降雨预报失误概率分析

3.1 降雨预报信息先验概率

互斥且完备的事件ei为流域降雨预报量级，根据不同量级降雨预报事件发生频次，利用古典频率公式，计算其发生的先验概率P(ei)，见表3。

表1 流域未来24 h降雨预报的“三率”分析Table 1 Rate analysis of rainfall forecast for the next 24 hours

表2 短期(24 h)降雨预报条件下实际降雨量统计参数及概率密度函数参数Table 2 Actual rainfall statistical parameters and probability density function parameters for the next 24 hours

表3 降雨预报信息先验概率Table 3 Prior probabilities of rainfall forecast information

3.2 设计洪水对应暴雨事件及条件概率

依据安康水库下游防洪标准及要求，以1983年洪水作为典型洪水过程，利用经验单位线，基于最小二乘法反推净雨，得净雨总量为116.49 mm，历时70 h，24 h最大净雨量为74.41 mm。由于研究区为湿润地区，多为蓄满产流，汛期下垫面接近饱和。为安全考虑，假定下垫面饱和，则净雨量即为暴雨量;以同倍比放大得到不同频率设计洪水对应24 h的暴雨量及对应事件 ，见表4。

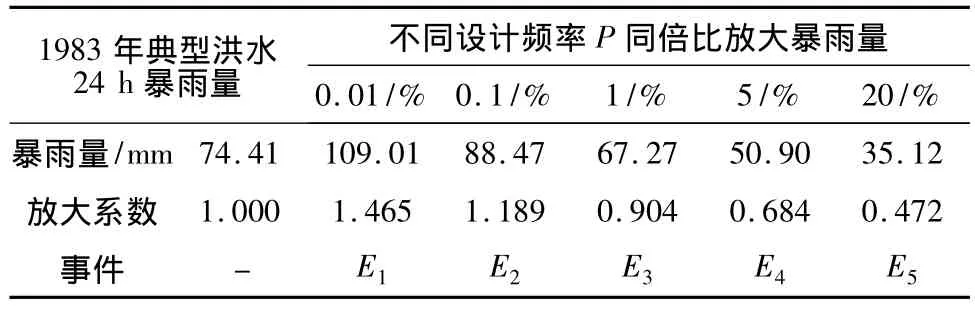
表4 不同设计频率洪水的暴雨量Table 4 Storm rainfall of different design flood frequency

根据表2参数，用P－Ⅲ型概率密度函数计算各量级降雨预报条件下未来24 h可能发生降雨的条件概率，见表5。

表5 降雨预报条件下未来24 h可能发生降雨的条件概率Table 5 Conditional probabilities of possible rainfall for the next 24 hours

3.3 各级降雨预报的后验概率

将表3和表5相应数据代入公式(1)，得到不同设计洪水对应暴雨事件Ej发生的条件下，各量级降雨预报的后验概率P(ei/Ej)，见表6。

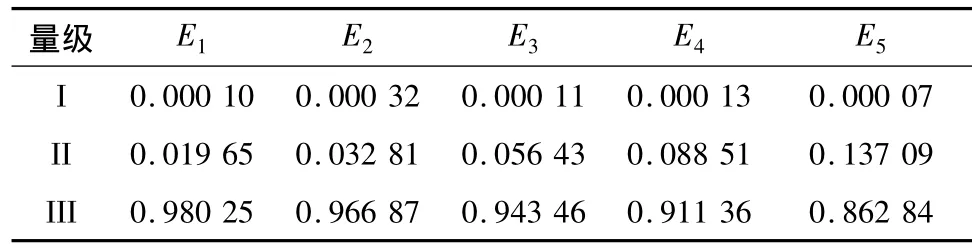
表6 各量级降雨预报的后验概率Table 6 Posterior probabilities of rainfall forecast information at different levels

表6可以看出，Ej事件发生的条件下，Ⅰ量级降雨预报的后验概率非常低，最高为0.032%，即Ej事件发生寄予Ⅰ量级降雨预报失误造成的几乎不可能，Ⅰ量级降雨预报失误对防洪预报调度风险发生没有影响。而Ⅱ量级和Ⅲ降雨预报的后验概率比较高，Ⅱ量级最高后验概率为13.7%，出现在E5事件发生的条件下，即为5年一遇洪水对应暴雨事件发生寄予Ⅱ量级降雨预报失误造成的概率较高，Ⅱ量级降雨预报失误对5年一遇洪水调度风险发生影响最大。Ⅲ量级最高后验概率达98.025%，出现在E1事件发生的条件下，即为万年一遇洪水对应暴雨事件发生寄予III量级降雨预报失误造成的概率最高，III量级预报失误对万年一遇洪水调度风险发生影响最大。因此，安康水库利用不同量级降雨预报信息实施防洪调度时，Ⅰ量级(预报无雨)降雨预报失误对水库调度影响不大，可指导水库优化调度，Ⅱ量级(预报小雨)降雨预报失误对小洪水调度影响较大，Ⅲ量级(预报中雨及以上)降雨预报失误对大洪水调度影响较大，可作为汛期水库优化调度的参考指标。

4 结论

本文分析了安康水库流域未来24 h降雨预报信息及其预报失误对安康水库防洪调度的影响，得到以下结论:

(1)流域未来24 h降雨预报信息可用，实际降雨分布服从P－Ⅲ型分布。

(2)在当前降雨预报水平下，Ⅰ量级(预报无雨)降雨预报失误对水库调度影响较小;Ⅱ量级(预报小雨)降雨预报失误对小洪水调度影响较大;Ⅲ量级(预报中雨及以上)降雨预报失误对大洪水调度影响较大。

(3)安康水库利用降雨预报信息实施防洪调度时，Ⅰ量级降雨预报信息可指导水库防洪调度，Ⅱ、Ⅲ量级降雨预报信息可作为水库防洪调度的参考指标。

［1］王本德，张艳平，李 敏，等.丹江口水库流域降雨预报漏报风险分析［J］.水电能源科学，2010，28(1):6－8.(WANG Ben-de，ZHANG Yan-ping，LI Min，et al.Risk Analysis of Missing Report of Rainfall Forecast in Danjiangkou Basin［J］.Water Resources and Power，2010，28(1):6 －8.(in Chinese))

［2］周惠成，李丽琴，胡 军，等.短期降雨预报在汛限水位动态控制中的应用［J］.水力发电，2005，31(8):22 －26.(ZHOU Hui-cheng，LI Li-qin，HU Jun，et al.Dynamic Control of Reservoir Normal Level in Flood Season Based on Short-term Rainfall Forecast［J］.Water Power，2005，31(8):22 －26.(in Chinese))

［3］王本德，周惠成，王国利，等.水库汛限水位动态控制理论与方法及其应用［M］.北京:中国水利水电出版社，2006:277 － 306.(WANG Ben-de，ZHOU Huicheng，WANG Guo-li，et al.Research on Dynamic Control of Reservoir Normal Elevation in Flood Season and Applications［M］.Beijing:China Water Power Press，2006:277 －306.(in Chinese))

［4］袁晶瑄，王本德，王福兴，等.基于短期降雨预报信息的水库汛期库水位实时动态控制方法研究［J］.水力发电学报，2008，27(4):15－19.(YUAN Jing-xuan，WANG Ben-de，WANG Fu-xing，et al.Study on Realtime Dynamic Operation of Reservoir Level in Flood Season Based on Short-term Rainfall Forecast Information［J］.Journal of Hydroelectric Engineering，2008，27(4):15 －19.(in Chinese))

［5］王本德，郭晓亮，周惠成，等.基于贝叶斯定理的汛限水位动态控制风险分析［J］.水力发电学报，2011，30(3):34 －38.(WANG Ben-de，GUO Xiao-liang，ZHOU Hui-cheng，et al.Risk Analysis on the Dynamic Control of Limit Water Level Based on Bayes Theorem［J］.Journal of Hydroelectric Engineering，2011，30(3):34－38.(in Chinese))

［6］刘 招，黄 强，于兴杰，等.基于6 h预报径流深的安康水库防洪预报调度方案研究［J］.水力发电学报，2011，30(2):4 － 10.(LIU Zhao，HUANG Qiang，YU Xing-jie，et al.A Flood Forecast Operation Scheme for Ankang Reservoir Based on Six Hours Runoff Forecast Information［J］.Journal of Hydroelectric Engineering，2011，30(2):4 －10.(in Chinese))

［7］魏永霞，王丽学.工程水文学［M］.北京:中国水利水电出版社，2005:66 －71.(WEI Yong-xia，WANG Lixue.Engineering Hydrology［M］.Beijing:China Water Power Press，2005:66 －71.(in Chinese))

［8］马江洪.概率统计教程［M］.北京:科学出版社，2007:18－19.(MA Jiang-hong.Tutorial of Probability Statistics［M］.Beijing:Science Press，2007:18 － 19.(in Chinese))

［9］宇世航.贝叶斯公式的教学方法［J］.高师理科学刊，2011，31(6):87 － 89.(YU Shi-hang.On the Teaching Method of Bayesian Formula［J］.Journal of Science of Teachers’College and University，2011，31(6):87 －89.(in Chinese))