蒙特卡罗随机统计技术在软件可靠性定量分析中的应用

林志鹏 （福建林业职业技术学院教务处，福建 南平353000）

在嵌入式软件开发过程中，涉及到在编写软件维护与测试说明书时，如何定量地描述软件可靠性的问题，而软件可靠性［1］是指在将要使用的指定环境下，软件能以用户可以接受的方式正确运行任务所表现出来的能力。从定量角度看，似乎应当是该软件在约定的环境条件下和在给定的时间区间内，按照软件规格说明的要求，成功地运行程序所规定功能的概率。

到目前为止，国内外建立的各种各样的软件可靠性分析模型已不下上百种［4］。而其中有一种错误随机植入模型——蒙特卡罗 （Monte Carlo）随机植入技术，就可很好地用于估算出被测程序模块中存在的错误数。

图1 蒙特卡罗技术求不规则图形面积

1 蒙特卡罗错误随机植入模型

用蒙特卡罗随机植入技术估算程序模块的错误数有以下几个优点：①工作方式相当直观，能在一定程度上反映出软件的质量；②虽然在技术上不完善，但至少产生了与软件质量相关的定量结果；③在最坏的情况下，起码可用来衡量“测试工作的有效性”，在某种程度上作为测试是否结束的一项标志［3］。

蒙特卡罗随机统计技术形象地举例如下，用它来确定不规则形状封闭图形面积，即采用一个大的矩形，把待测的封闭图形完全包围在该大矩形的内部，如图1所示。由计算机大量生成该矩形内均匀分布的“点”，然后清点在大矩形内“点”的总个数和在封闭图形内“点”的个数，可近似得到以下表达式：

把上面思路应用在软件可靠性分析中，可将错误随机植入模型定义如下：

定义1（蒙特卡罗错误植入模型） 为估算某种软件所含有固有错误的具体数目N，可在该软件中人为随机植入NS个错误数，然后进行软件测试。如果通过测试发现M个固有错误，则其中发现的人为随机植入错误数有MS个。

假设测试过程中未引入新的错误，可以进一步假设，人为随机植入NS个错误数后，在故障的出现概率等同于植入错误数之前故障的出现概率，即将程序模块单位长度故障率认为是一个常数。

将“软件固有错误数N”看成是“封闭图形的面积”，将“人为植入错误数NS”看成是“已知的大矩形的面积”；将“测试中发现的固有错误数M”、“测试中发现的人为植入错误数MS”，分别看成是“在封闭图形内点的个数”、“大矩形内点的个数”，由此得出蒙特卡罗错误植入模型为：

例1 假设某企业单位在开发一个嵌入式实时应用软件宽带路由器的NanOS程序，其长度（机器指令条数）为105。现随机地人为植入10个错误，然后由一个测试组进行测试，假设结果一共发现有160个错误，其中有2个是人为播种植入的错误。定义1中的式（1）蒙特卡罗错误植入模型估算出被测程序模块中将会遗留下多少个未被发现的隐藏错误。

整理例1的数据，得NS＝10，M＝160，MS＝2。于是可估算出程序中错误的总数N：

这时被测程序模块中将会遗留下未被发现的隐藏错误数Nt：

2 Hyman分别测试法

蒙特卡罗错误随机植入模型存在以下3个方面的局限性：①由于所有错误不可能等概率出现，而且错误有着连带性 （一个错误可能隐藏另一个错误），因此要想使随机植入的错误有助于正确地推算出固有的错误数时，如何有效地在程序模块中选择和植入这类错误相对很困难［5］。②在检测错误时，错误一般不会等概率地被发现，而且在修复错误时也经常会引出一些新的错误，可见很难用简单的公式获得很理想的估计值。③随机植入的错误本身会增加检测发现错误和修改错误的工作量。为此，特提出Hyman分别测试法作为“错误随机植入”测试方法的补充。

由A和B两组测试人员同时相互独立地测试例1中的NanOS程序某个模块的2个拷贝，进行如下符号假设：将A、B两个测试小组发现的错误数分别看成是2个“独立”事件，记N为宽带路由器NanOS程序中被测程序模块存在的故障总数；NA为A组检测到的错误数；P（A）为A组检测到的错误数在被测程序模块故障总数中发生的概率；NB为B组检测到的错误数；P（B）为B组检测到的错误数在被测程序模块故障总数中发生的概率；NAB为A、B两组发现的相同错误数；P（A∩B）为A、B两组发现的相同错误数发生的概率。

根据事件A、B相互独立的充分必要条件P（A∩B）＝P（A）P（B），得：

即：

假设经过2周测试后，A组发现错误总数NA为350个，B组发现错误总数NB为320个，其中2组发现的相同错误数目NAB为132个。利用式（2）计算：

即估算出测试前该程序原有错误数为849个，比蒙特卡罗错误随机植入模型的估算结果更为接近实际值。需注意运用Hyman分别测试法方案的前提：①2组发现的不同错误数所占比例相对较低；②2周来发现的错误在全部错误中有着代表性。另外，由于目前所进行的仅仅是模块测试，即部件级测试，还没有考虑到集成测试和系统测试中将必然会出现的NanOS程序错误数量，因此，可预知总的NanOS程序错误数必然大于849个。

3 软件可靠性定量分析

在软件可靠性定量分析［6］中，可以借用硬件的MTBF（平均无故障时间）或者MTTF（失效的平均等待时间）作为软件可靠性的主要指标。平均无故障时间 （MTBF）与单位长度的剩余故障个数εr成反比，即：

式中，K的典型值取为200。

通过测试一段时间后，在NanOS程序中发现795个固有错误，且及时改正测试中发现的错误。就可利用式 （3）计算出NanOS程序的平均无故障时间。

由例1，设已知被测程序长度L＝105，已检测到且修正过错误数EC＝795，根据公式应用蒙特卡罗错误随机植入模型，得N＝800个，所以由式（3）可得宽带路由器NanOS程序的平均无故障时间MTBF值：

由此看出软件可靠性MTBF是用户可预测性和软件中存在各类错误的一个复杂函数。即使2个软件用来提供同样功能并有着相同错误数目，在不同用户使用情况下也会有不同的MTBF（与用户的可预测性有关）；功能上大体相同的2个软件，在相同用户条件下，由于软件有不同错误数，因此也会得到不同的MTBF值 （此时错误数起主要作用）。

如要将该软件可靠性再提高4倍，即MTBF＝500h，则由式 （4）变型得：

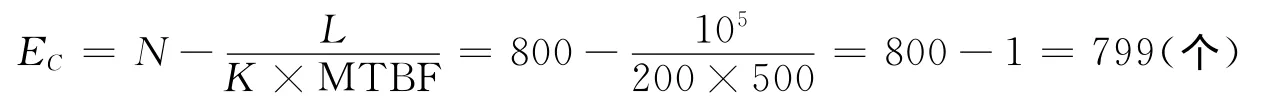
由于已检测到且修正过的错误数目为795个，因此再需要改正的错误个数是799－795＝4个，就将该软件可靠性再提高4倍。

4 结 语

如何提高软件质量是软件工程的一个重要研究课题，而软件可靠性定量分析工作是保证软件质量的一个重要措施［6］。笔者示范了一种应用蒙特卡罗错误随机统计模型方法，并给出了应用此方法的宽带路由器NanOS程序可靠性定量分析具体实例。并基于Hyman分别测试方案对蒙特卡罗方法进行补充［7］，该测试估算方法，对软件可靠性定量分析提供了有力保障。通过该可靠性定量分析方法，强有力地支撑软件质量提升。

［1］王立福.软件工程 ［M］.北京：北京大学出版社，2002.

［2］张海藩 .软件工程 ［M］.北京：人民邮电出版社，2002.

［3］尹增谦 .蒙特卡罗方法及应用 ［J］.物理与工程，2002，12 （3）：45－49.

［4］马海云，党建武 .一种加速软件可靠性测试的技术研究 ［J］.工业仪表与自动化装置，2011（3）：6－9.

［5］徐钟济 .蒙特卡罗方法 ［M］.北京：高等教育出版社，1985.

［6］朱少民 .软件测试方法和技术 ［M］.北京：高等教育出版社，2005.

［7］马海云 .基于蒙特卡罗的软件可靠性测试技术的研究与实现 ［J］.郑州大学学报 （工学版），2007（4）：28－29.