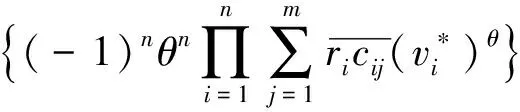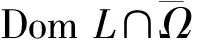具多时滞和离散时间非自治互惠系统的正周期解
郭 微
(北华大学 数学学院, 吉林 吉林 132013)
0 引 言
近年来, 关于非自治生物动力系统正周期解的研究已取得许多结果[1-4]. May[5]建立了两种群互惠系统, 柏灵等[6]对文献[5]的互惠系统进行了离散化并给出了系统正周期解存在的充分条件. 于丽颖[7]将文献[6]的差分系统推广到多种群情形, 并给出了系统正周期解存在的充分条件. 基于此, 本文综合考虑种群受自身遗传因素和环境污染及有毒物的影响, 建立如下连续时间的非自治多时滞互惠系统:
其中:xi(t)表示i种群在时刻t的密度;ri,ai,bis,cij∈C([0,+∞),(0,+∞))(s,i=1,2,…,n,s≠i)均为ω>0的周期函数;θ为正常数.
为方便, 本文中i=1,2,…,n简记为i, 记 Z,Z0,Z+分别表示所有整数集、 非负整数集和正整数集, 对给定的某个函数g,
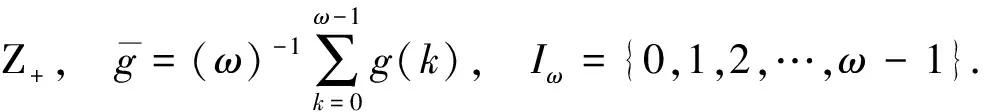
利用与文献[8]相同方法, 易得如下带有周期系数和离散时间的非自治多时滞互惠系统:
(1)

基于差分互惠系统(1)的生物学意义, 仅讨论

的情形. 对差分互惠系统(1), 考虑初值问题:
xi(υ)=φi(υ)≥0,υ∈[-τ,0],xi(0)>0,
(2)
其中τ=max{τ1,τ2,…,τm}. 对给定的某个函数f,
本文利用重合度理论中延拓定理证明差分互惠系统(1)正周期解的存在性. 易见, 当i=2,τj=0,θ=1时, 差分互惠系统(1)即为文献[6]的两种群差分互惠系统; 当τj=0,θ=1时, 差分系统(1)即为文献[7]的多种群互惠差分系统. 因此, 差分互惠系统(1)改进了文献[5-7]中的生态数学模型, 更具有实际生态意义.
1 引 理

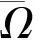
1) 对任意的λ∈(0,1), 算子方程Ly=λNy的解满足y∉∂Ω;
2) 对任意的y∈∂Ω∩KerL,QNy≠0, 且deg{JQN,Ω∩KerL,0}≠0.
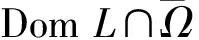
引理3[8]设g: Z →R,g(k+ω)=g(k),ω是正整数, 则对任意的k1,k2∈Iω及任意的k∈Z, 有
引理4存在一个与参数μ无关的常数M0, 对方程组
(3)

2 主要结果

证明: 做变换xi(k)=exp{yi(k)}, 则差分互惠系统(1)可改写为
(4)

Rn,k∈Z},
令L:lω→lω是差分算子: (Ly)(k)=y(k+1)-y(k),y∈lω,k∈Z . 再令
则


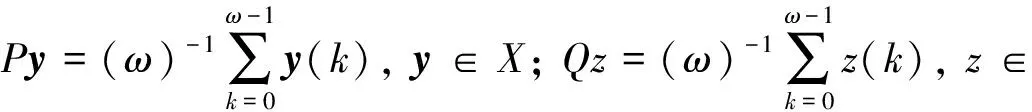
ImP=KerL, ImL=KerQ=Im(I-Q),
因此,L的逆映射Kp: ImL→DomL∩KerP存在,
于是
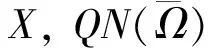
下面寻找一个适当的有界开集Ω满足引理2的条件. 相应于算子方程Ly=λNy,λ∈(0,1), 有
(5)

(6)
则由式(5),(6)知
(7)
一方面, 由式(6)有
从而有
结合式(7), 由引理3, 有
(8)
另一方面, 由式(6)又有
从而有
同理, 结合式(7)和引理3, 有
(9)
于是, 由式(8),(9)可得
(10)
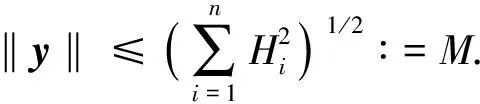
(11)
显然,M与λ的选取无关. 令B>max{M0,M},Ω={y=(y1,y2,…,yn)T∈X‖y‖ 构造同伦映射hμ(y)=μQNy+(1-μ)Gy,μ∈[0,1], 其中 注1由上述讨论可知, 如果差分互惠系统(1)中的常数时滞改为时变时滞, 则定理1的结论仍然成立, 表明时滞对系统是无害的. 注2定理1的结论表明, 差分互惠系统(1)一定会产生周期性生物振荡现象, 且时滞对系统正周期解的存在性无影响. [1] ZHAO Ming, CHENG Rong-fu. Existence of Periodic Solution of a Food Chain System with Biocontrol and Ratio Functional Response [J]. Journal of Jilin University: Science Edition, 2009, 47(4): 730-736. (赵明, 程荣福. 一类具生物控制和比率型功能反应的食物链系统周期解的存在性 [J]. 吉林大学学报: 理学版, 2009, 47(4): 730-736.) [2] WEN Shao-xiong, FAN Meng. Existence of Periodic Solution of Apredator-Prey System with Hassell-Varley Functional Response [J]. Journal of Northeast Normal University: Natural Science Edition, 2011, 43(1): 10-15. (温绍雄, 范猛. 具有Hassell-Varley型功能性反应的捕食者-食饵系统周期解的存在性 [J]. 东北师大学报: 自然科学版, 2011, 43(1): 10-15.) [3] CHENG Rong-fu, CHANG Liang. Multiple Periodic Solution of a Predator-Prey System with Infinite Delay and Non-monotonic Functional Response [J]. Journal of Jilin University: Science Edition, 2010, 48(5): 761-765. (程荣福, 常亮. 具无限时滞和非单调功能性反应的捕食系统的多周期解 [J]. 吉林大学学报: 理学版, 2010, 48(5): 761-765.) [4] CHENG Rong-fu. Existence of Positive Periodic Solution for a Predator-Prey Model with Bio-controls and Several Delays [J]. Journal of Beihua University: Natural Science, 2010, 11(1): 1-6. (程荣福. 一类具生物控制的多滞量捕食模型正周期解的存在性 [J]. 北华大学学报: 自然科学版, 2010, 11(1): 1-6.) [5] May R M. Theoretical Ecology: Principles and Applications [M]. Oxford: Blackwell Scientific, 1976. [6] BAI Ling, FAN Meng, WANG Ke. Existence of Periodic Solutions for Difference Equations of a Cooperative Systems [J]. Journal of Biomathematics, 2004, 19(3): 271-279. (柏灵, 范猛, 王克. 离散时间的互惠系统的正周期解的存在性 [J]. 生物数学学报, 2004, 19(3): 271-279.) [7] YU Li-ying. Existence of Periodic Solutions for a Discrete Time of Many Species Cooperative Systems [J]. Journal of Beihua University: Natural Science, 2011, 12(6): 627-631. (于丽颖. 离散时间的多种群互惠系统正周期解的存在性 [J]. 北华大学学报: 自然科学版, 2011, 12(6): 627-631.) [8] FAN Meng, WANG Ke. Periodic Solutions of a Discrete Time Nonautonomous Ratio-Dependent Predator-Prey Systems [J]. Mathematical and Computer Modelling, 2002, 35: 951-961. (范猛, 王克. 离散时间的非自治比率依赖的捕食者-食饵系统的周期解 [J]. 数学与计算机模拟, 2002, 35: 951-961.) [9] Gaines R E, Mawhin J L. Coincidence Degree and Nonlinear Differential Equations [M]. Berlin: Springer-Verlag, 1997: 56-69. [10] ZHANG Rui-yang. Periodic Solutions of a Single Species Discrete Population Model with Periodic Harvest/Stock [J]. Computers and Mathematics with Applications, 2002, 39(1): 77-90. (张瑞阳. 具有周期收获或存放的单种群不连续的人口模型的周期解 [J]. 计算机与数学及其应用, 2002, 39(1): 77-90.)