一类渐近线性波方程的非平凡时间周期解

常小军,路京京

(1. 吉林大学 数学学院,长春 130012;2. 吉林大学 金融学院,长春 130012)

0 引 言

考虑如下非线性波方程:

(1)

其中f∈C([0,π]×R2,R)且f关于t是2π-周期的.

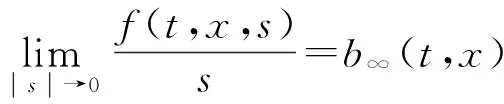
记‖·‖r为空间Lr(Q)(r∈[1,∞))中范数,(·,·)r为相应的内积. 定义Banach空间

其上的范数为

显然,E具有分解E=E-⊕E0⊕E+. 定义E上的对偶

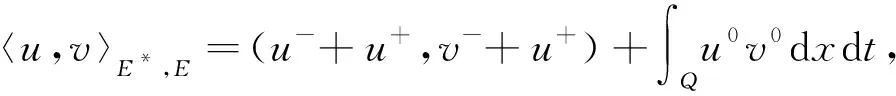
其中

定义作用泛函Φ:E→ R,

(2)

由(2)可得Φ∈C1(E,R). 显然,Φ是强不定的泛函,并且Φ的临界点对应于式(1)的弱解,即

(3)

令X={u∈E:u(t,x)=u(π+t,π-x)},则X是E的闭子空间且X∩Ker□={0}. 显然,X紧嵌入到Lr(R)(∀r≥1),且X在□及f的作用下是不变的. 因此Φ|X的临界点即为Φ的临界点. 不妨记Φ|X为Φ,X+=X∩E+,X-=X∩E-,则有X=X-⊕X+. 在X上定义范数‖u‖X≐‖u‖E. 显然,X是Banach空间,将其记为 ‖·‖. 重排□的特征值: …≤λ-,3≤λ-,2≤λ-,1<0<λ+,1≤λ+,2≤λ+,3≤…,相应的特征函数分别记为ψ-,i,ψ+,k,i,k∈Z+.

1 主要结果

定理1假设下面条件满足,则问题(1)存在非平凡弱解:

1) 存在a1,a2>0,使得对于一致的(t,x)∈Q,有|f(t,x,s)|≤a1|s|+a2,∀s∈R;

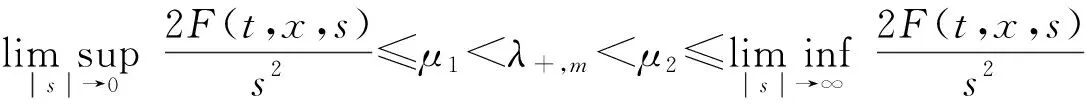
5)f(t,x,s)=f(π+t,π-x,s),∀(t,x,s)∈Q×R.

注1由于波算子□的核空间是无穷维的,通常要求f(t,x,s)关于s是单调函数. Coron[11]通过引入取不变子空间的技巧在不要求f单调的情形下研究了问题(1). 本文结合Coron的技巧研究问题(1),因此不要求f满足单调性条件. 此外,这里不要求比率f(t,x,s)/s在s充分大时有极限,并且不要求f在无穷远处满足共振或非共振条件,从而f(t,x,s)/s在s充分大时可能跨越波算子□的多个特征值.

注2Costa等[12]在如下非二次条件下,结合定理1中的条件2),3)研究了问题(1)非平凡弱解的存在性:

关于 a.e. (t,x)∈Q一致成立,

且有

关于 a.e. (t,x)∈Q一致成立,

或

关于a.e. (t,x)∈Q一致成立.

显然定理1的条件4)弱于非二次条件.

下面应用强不定泛函的临界点理论证明定理1. 类似于文献[12]中定理2.10的证明,只需证明泛函Φ有鞍点结构并且满足(C)c条件. 证明分两个步骤: 泛函Φ有鞍点结构和泛函Φ满足紧性条件.

引理1在定理1的假设下,泛函Φ有鞍点结构.

证明: 由条件1)～3)知,存在ρ1,ρ2∈R,使得μ1<ρ1<λ+,m<ρ2<μ2,并且存在p>2和Cp>0,使得

∀(t,x,u)∈Q×R.

对任意的j∈Z+,记Ej=X-⊕span{φ+,1,…,φ+,j}. 对任意的u∈(Em-1)⊥,

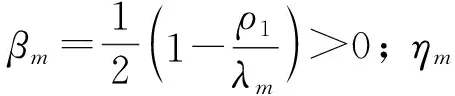
Φ(u)≥δm, ∀u∈(Em-1)⊥, ‖u‖=rm.

易见,存在充分大的Rm>0,使得当u∈Em且满足‖u‖≥Rm时,有Φ(u)≤0. 证毕.

引理2在定理1的假设下,对任意的c∈R,泛函Φ满足(C)c条件.

证明: 令{un}⊂X满足

Φ(un)→c, (1+‖un‖)Φ′(un)→0.

(4)

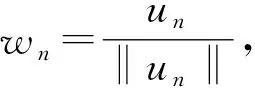
矛盾. 因此,w0≠0. 从而|un(t,x)| → +∞,∀(t,x)∈Q*,其中Q*∶={(t,x)∈Q:w0(t,x)≠0}. 结合假设条件1)和4),存在M>0,使得

矛盾. 因此{un}在X中有界. 进而利用X紧嵌入到Lr(Q)(r≥1)可知,存在u0∈X,使得在X中un→u0. 证毕.

下面证明定理1. 由引理1知,存在泛函Φ的(C)c序列{un}使得c>0. 利用引理2,序列{un}在X中是一致有界的,且有u0∈X,使得在X中un→u0. 再利用标准的讨论[12],可得Φ(u0)=c,并且有

∀φ∈X.

从而u0是问题(1)的非平凡弱解.

[1] Anane A,Chakrone O,Zerouali A. Nonresonance Conditions for a Nonlinear Hyperbolic Problem [J]. Adv Dyn Syst Appl,2007,2(1): 31-40.

[2] GUO Yu-xia,LIU Jia-quan. Periodic Solutions for an Asymptotically Linear Wave Equation with Resonance [J]. Nonlinear Analysis: Theory,Methods &Applications,2007,67(9): 2727-2743.

[3] Girão P,Tehrani H. On the Fucik Spectrum of the Wave Operator and an Asymptotically Linear Problem [J]. J Math Anal Appl,2010,366(1): 55-66.

[4] JI Shu-guan,LI Yong. Time Periodic Solutions to the One-Dimensional Nonlinear Wave Equation [J]. Arch Ration Mech Anal,2011,199(2): 435-451.

[5] Rudakov I A. Periodic Solutions of a Quasilinear Wave Equation with Homogeneous Boundary Conditions [J]. J Math Sci,2008,150(6): 2588-2597.

[6] Tanaka M. Application of Local Linking to Asymptotically Linear Wave Equations with Resonance Ⅱ [J]. SUT J Math,2004,40(2): 157-179.

[7] Tanaka M. Existence of Multiple Weak Solutions for Asymptotically Linear Wave Equations [J]. Nonlinear Analysis: Theory,Methods &Applications,2006,65(2): 475-499.

[8] CHANG Xiao-jun,LI Yong. Existence and Multiplicity of Nontrivial Solutions for Semilinear Elliptic Dirichlet Problems across Resonance [J]. Topol Methods Nonlinear Anal,2010,36(2): 285-310.

[9] LIU Zhao-li,SU Jia-bao,WANG Zhi-qiang. A Twist Condition and Periodic Solutions of Hamiltonian Systems [J]. Advin Math,2008,218(6): 1895-1913.

[10] LIU Zhao-li,SU Jia-bao,WANG Zhi-qiang. Solutions of Elliptic Problems with Nonlinearities of Linear Growth [J]. Calc Var Partial Differ Equat,2009,35(4): 463-480.

[11] Coron J M. Periodic Solutions of a Nonlinear Wave Equation without Assumption of Monotonicity [J]. Math Ann,1983,262(2): 273-285.

[12] Costa D G,Magalhães C A. A Unified Approach to a Class of Strongly Indefinite Functionals [J]. J Differential Equations,1996,125(2): 521-547.