非光滑广义凸多目标规划的对偶

王彩玲,王泽升

(吉林大学 数学学院,长春 130012)

非光滑多目标优化理论应用广泛,而广义凸性在对偶理论中具有重要作用,已广泛用于解决优化问题.文献[1-6]给出了不同条件下广义凸函数的最优性条件与对偶理论.本文通过定义复合Q-ρ不变凸和S-δ不变凸函数,对其构成的不可微复合凸多目标规划问题给出了新的对偶理论,推广了文献[3-7] 的结果.设Q⊂p和S⊂m分别是具有内部的闭凸锥.

1 基本概念

考虑复合多目标规划问题(VP):

其中:g(G(x))=(g1(G1(x)),…,gm(Gm(x)))T;x∈X(X是Banach空间);f和g分别是n上实值局部Lipschitz向量函数;Fi和Gj:X→n分别是局部Lipschitz函数和Gateaux可微函数,它们的Gateaux导数分别记为(·)(i=1,2,…,p；j=1,2,…,m).记

Ω={x∈X|-g(G(x))∈S},

Q*和S*分别为Q和S的对偶锥,如Q*={λ∈p|λTv≥0,∀v∈Q}.

定义1如果存在ρ∈p,使得对∀及∀有

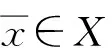
定义2如果存在δ∈m,使得对∀及∀有

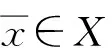
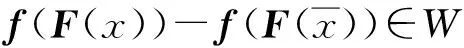
其中U=W∩(-W).

2 对偶定理

考虑(VP)的Mond-Weir型对偶问题(VD):

定理1(弱对偶性) 设x和(y,Λ)分别是(VP)和(VD)的可行解,如果f(F)在y处关于函数η和θ：X×X→X是广义复合Q-ρ不变凸的,g(G)在y处关于函数η和θ是广义复合S-δ不变凸的,且ρ+Λδ∈Q,则

f(F(x))-f(F(y))∈W.

证明：由已知条件可得

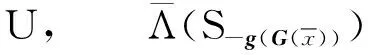
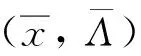
由于对任意(VD)的可行解(y,Λ),由定理1可得

证明：由已知条件及定理1可知,对∀x∈Ω,有

⊂W.

[1] Mishra S K,WANG Shou-yang,LAI Kin-keung.Nondifferentiable Multiobjective Programming under Generalizedd-Univexity [J].European Journal of Operation Research,2005,160(1): 218-226.

[2] Mishra S K,WANG Shuo-yang,LAI Kin-keung.Generalized Convexity and Vector Optimization [M].Nonconvex Optimization and Its Applications.Vol.90.Berlin: Springer-Verlag,2009.

[3] YANG Xin-min,Teo K L,YANG Xiao-qi.Duality for a Class of Nondifferentiable Multiobjective Programming Problems [J].J Math Anal Appl,2000,252(2): 999-1005.

[4] Mishra S K,Giorgi G,WANG Shou-yang.Duality in Vector Optimization in Banach Spaces with Generalized Convexity [J].Journal of Global Optimization,2004,29(4): 415-424.

[5] Niculescu C.Optimality and Duality in Multiobjective Fractional Programming Involvingρ-Semilocally Type Ⅰ-Preinvex and Related Functions [J].J Math Anal Appl,2007,335(1): 7-19.

[6] Shapiro A.On a Class of Nonsmooth Composite Functions [J].Mathematics of Operational Research,2003,28(4): 677-692.

[7] Jeyakumar V,Yang X Q.Convex Composite Multiobjective Nonsmooth Programming [J].Math Programming,1993,59(1/2/3): 325-343.

[8] WANG Cai-ling.Saddle-Point Theory of Nonsmooth Invex Multiobjective Programming [J].Journal of Jilin University: Science Edition,2011,49(4): 693-695.(王彩玲.非光滑凸多目标规划的鞍点定理 [J].吉林大学学报: 理学版,2011,49(4): 693-695.)