变系数Wave-Like方程的格子Boltzmann模型

史秀波,闫广武

(1.桂林理工大学 理学院,广西 桂林 541004； 2.吉林大学 数学学院,长春 130012)

格子Boltzmann方法(LBM)作为一种新的数值方法在计算流体力学、 非线性偏微分方程等领域应用广泛[1-6].闫广武等[7-10]将这种方法应用于波传播问题,为研究其他波动问题提供了可选择的途径.在科学工程领域,许多物理问题都可以借助变系数初边值问题描述,这些线性和非线性模型及其解析解或数值解对应用科学具有重要意义[11].本文用格子Boltzmann方法对如下变系数wave-like方程进行模拟研究:

(1)

其中f(x),g(x)和h(x)是关于x,y,z的函数.

方程(1)可以表示成如下形式：

(2)

这里:

Cs(x)=f(x)+g(x)+h(x);

u(x,t)的下一个时间步表达式[7]为

(3)

本文用格子Boltzmann方法为方程(2)建立了格子Boltzmann模型.通过使用Chapman-Enskog展开和多尺度技术,获得了系列格子Boltzmann偏微分方程[12]、 平衡态分布函数的高阶矩以及宏观变系数wave-like方程.数值实验表明,模拟结果与解析解吻合较好.

1 格子Boltzmann模型

选择二维5-bit网格和三维7-bit网格,分布函数fα(x,t)定义为在某节点x上、t时刻、 具有速度eα(α=0,1,…,b)的粒子出现的概率,其中α=0表示静止粒子.在二维空间中,b=4,粒子速度为

eα={(0,0),(c,0),(0,c),(-c,0),(0,-c)}；

三维空间中,b=6,粒子速度为

eα={(0,0,0),(c,0,0),(0,c,0),(0,0,c),(-c,0,0),(0,-c,0),(0,0,-c)},

其中c表示速率.定义宏观量:

(4)

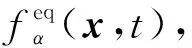
(5)

格子Boltzmann方程表示为

fα(x+eα,t+1)-fα(x,t)=Ωα+ωα,

(6)

选取Knudsen数ε作为数值模拟的时间步长和Chapman-Enskog展开的小参数[13],在该尺度上,方程(6)可写为

fα(x+εeα,t+ε)-fα(x,t)=Ωα+ωα,

(7)

其中

ωα(x,t)=ε2θα(x,t).

(8)

通过Chapman-Enskog展开和时间多尺度可获得不同时间尺度上的系列格子Boltzmann偏微分方程：

(9)

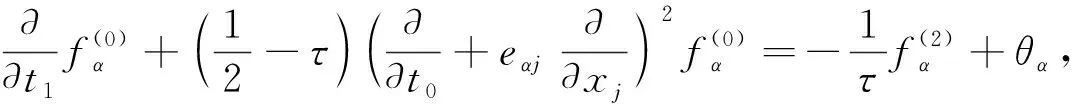
(10)

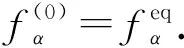
为了获得平衡态分布函数,选取高阶矩为

(14)

当选取

(15)

且假设附加分布函数θα和α无关,并取

(16)

后,即得宏观变系数wave-like方程(2).

结合式(5),(12),(13),可得平衡态分布函数的表达式为

其中D表示空间维数.

进行数值计算时,迭代过程分为如下两步：

1) 碰撞：

(19)

2) 流：

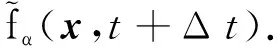
(20)

(21)

为了对模型进行误差分析,将式(9)+式(10)×ε+式(11)×ε2,并对两端关于α求和有

(22)

由于附加分布函数θα不是一个正常尺度上的量,因此导致误差出现反弹现象,使模型的精度最后降为一阶.

2 数值模拟

为了验证模型的效果,本文分别对二维和三维变系数wave-like问题进行数值模拟.对二维问题使用5-bit模型,三维问题使用7-bit模型.

2.1 二维初边值问题

二维初边值问题(initial boundary value problems,IBVP):

Neumann边界条件为

初始条件为

u(x,y,0)=x4,ut(x,y,0)=y4;

(24)c

精确解[14]为

u(x,y,t)=x4cosht+y4sinht.

(24)d

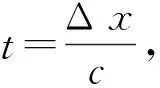
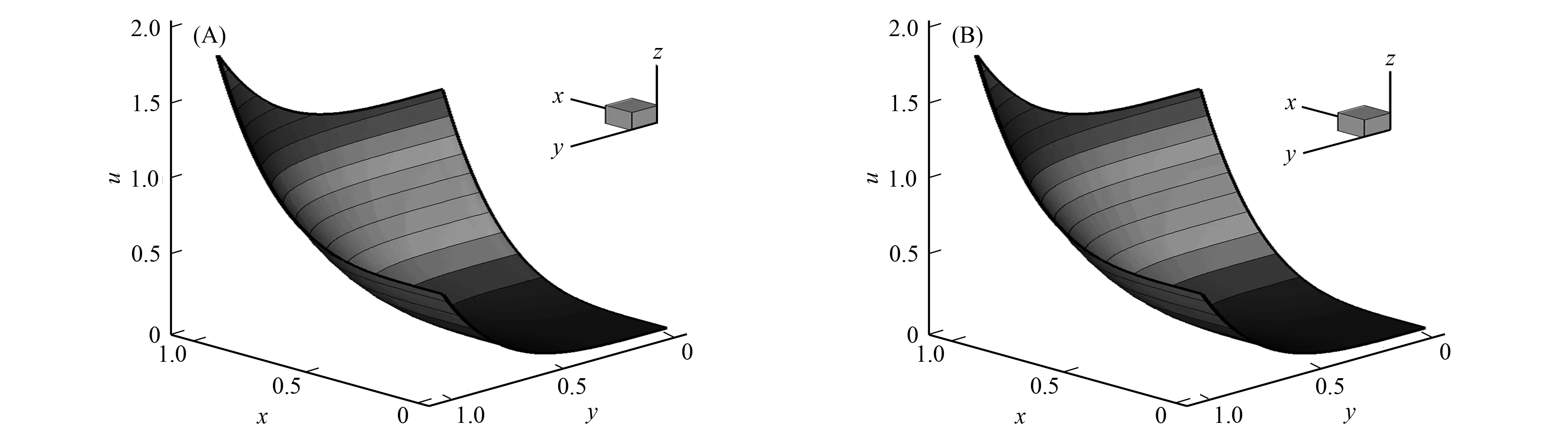
图1 t=0.6时初边值问题(24)的LBM解(A)和精确解(B)Fig.1 LBM solution (A) and exact solution (B) for IBVP(24) at t=0.6

2.2 三维非齐次IBVP

三维非齐次IBVP:

Dirichlet边界条件为

初始条件为

u(x,y,z,0)=0,ut(x,y,z,0)=x2+y2-z2;

(25)c

精确解[14]为

u(x,y,z,t)=(x2+y2)et+z2e-t-(x2+y2+z2).

(25)d

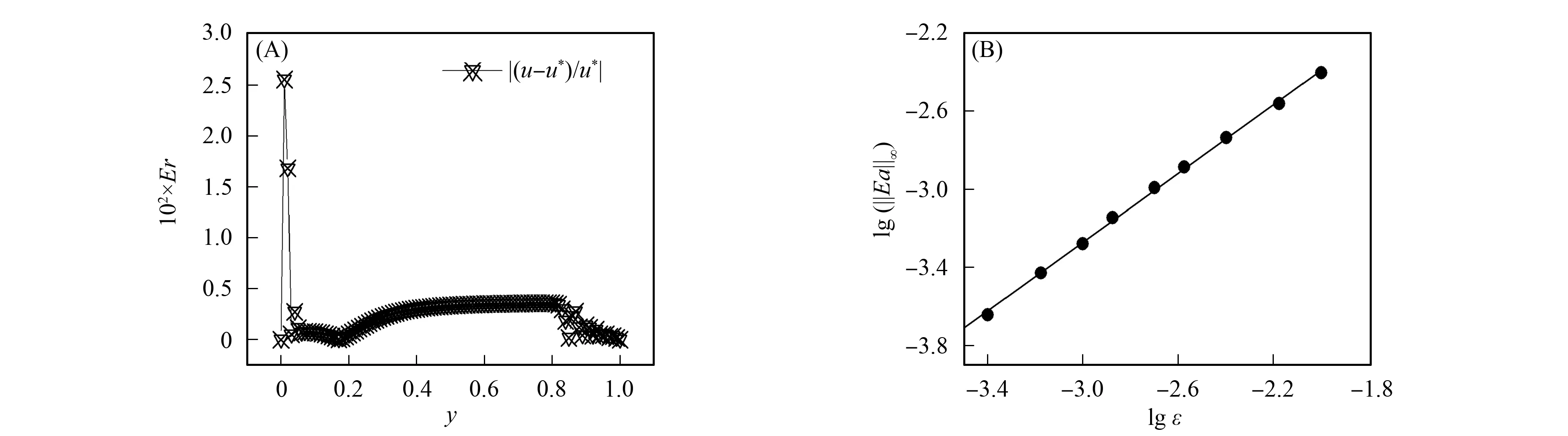
图2 t=0.6时初边值问题(24)在x=0.2处的相对误差曲线(A)及 绝对误差无穷模和Knudsen数ε的对数关系曲线(B)Fig.2 Curves of the relative error (A) and logarithmic relationship curves for IBVP(24) of the infinite norm of the absolute error Ea versus the Knudsen number ε at t=0.6,on x=0.2

参数设置为：格子尺寸50×50×50,c=5.0,τ=1.01,t=2.0.图3(A)和(B)分别为三维非齐次IBVP(25)格子Boltzmann模型的数值解u和精确解u*.图4(A)和(B)分别为三维非齐次IBVP(25)两种结果在t=2时的相对误差Er=|(u-u*)/u*|曲线及相对误差的无穷模和Knudsen数ε的对数关系曲线.

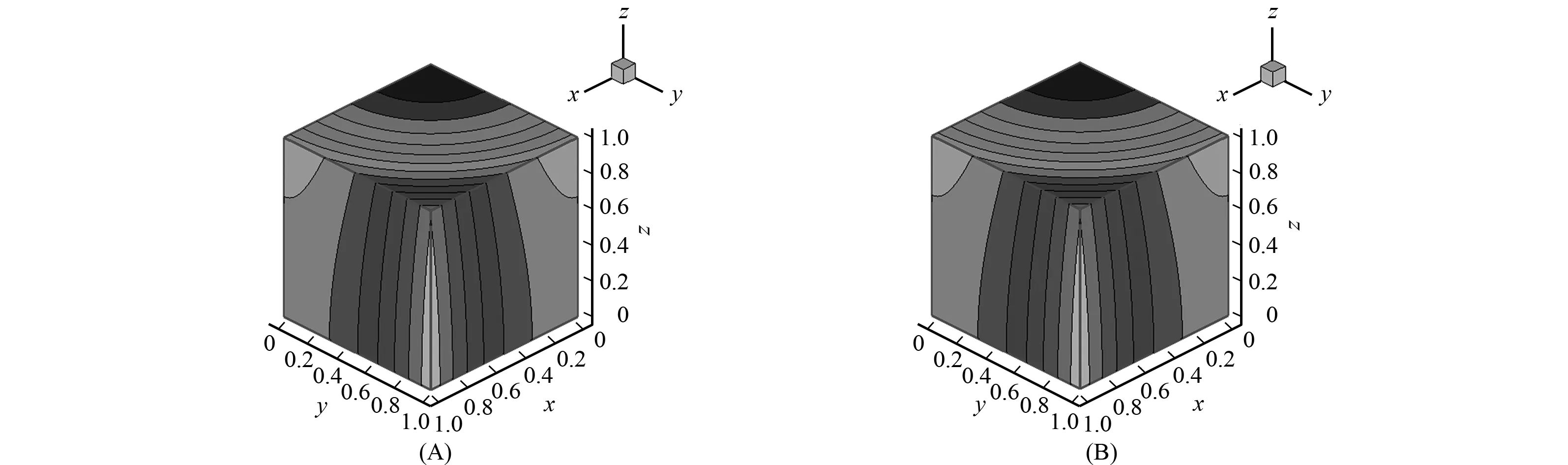
图3 t=2时初边值问题(25)的LBM解(A)和精确解(B)Fig.3 LBM solution (A) and exact solution (B) for IBVP(25) at t=2

图4 t=2时初边值问题(25)在x=0.6,z=0.6处的相对误差曲线(A)及 相对误差无穷模和Knudsen数ε的对数关系曲线(B)Fig.4 Curves of the relative error (A) and logarithmic relationship curves (B) for IBVP(25) of the infinite norm of the relative error Er versus the Knudsen number ε at t=2,on x=0.6,z=0.6

由图3和图4可见,LBM解与精确解基本一致.由图4(A)可见,误差在(0,0.022 5)范围内,表明数值解与精确解吻合较好.由图4(B)可见,本文模型的误差对网格数有依赖关系,网格越密,模型的误差越小,表明LBM模型是收敛的.数值实验表明,LBM是用于模拟wave-like方程的一种有效方法.

[1] QIAN Yue-hong,D’Humieres D,Lallemand P.Lattice BGK Model for Navier-Stokes Equations [J].Europhysics Letters,1992,17(6): 479-484.

[2] Benzi R,Succi S,Vergassola M.The Lattice Boltzmann Equation: Theory and Applications [J].Physics Report,1992,222: 145-197.

[3] CHEN Shi-yi,Doolen G D.Lattice Boltzmann Method for Fluid Flow [J].Annual Review of Fluid Mechanics,1998,30: 329-364.

[4] Palpacelli S,Succi S.Quantum Lattice Boltzmann Simulation of Expanding Bose-Einstein Condensates in Random Potentials [J].Physical Review E,2008,77: 066708.

[5] SHI Yong,Peter L B,Ying W Y,et al.Accuracy of the Lattice Boltzmann Method for Low-Speed Noncontinuum Flows [J].Physical Review E,2011,83: 045701.

[6] Dellar P J,Lapitski D,Palpacelli S,et al.Isotropy of Three-Dimensional Quantum Lattice Boltzmann Schemes [J].Physical Review E,2011,83: 046706.

[7] YAN Guang-wu.A Lattice Boltzmann Equation for Waves [J].Journal of Computational Physics,2000,161(1): 61-69.

[8] ZHANG Jian-ying,YAN Guang-wu,SHI Xiu-bo.Lattice Boltzmann Model for Wave Propagation [J].Physical Review E,2009,80: 026706.

[9] SHI Xiu-bo,YAN Guang-wu,ZHANG Jian-ying.A Multi-energy-level Lattice Boltzmann Model for Two-Dimensional Wave Equation [J].International Journal for Numerical Methods in Fluids,2010,64(2): 148-162.

[10] ZHANG Jian-ying,YAN Guang-wu,YAN Bo,et al.A Lattice Boltzmann Model for Two-Dimensional Sound Wave [J].International Journal for Numerical Methods in Fluids,2011,67: 214-231.

[11] Allahviranloo T,Abbasbandy S,Rouhparvar H.The Exact Solutions of Fuzzy Wave-Like Equations with Variable Coefficients by a Variational Iteration Method [J].Applied Soft Computing,2011,11(2): 2186-2192.

[12] ZHANG Jian-ying,YAN Guang-wu.Lattice Boltzmann Method for One and Two- Dimensional Burgers Equation [J].Physica A: Statistical Mechanics and Its Applications,2008,387(19/20): 4771-4786.

[13] Chapman S,Cowling T G.The Mathematical Theory of Non-uniform Gas [M].Cambridge: Cambridge University Press,1939.

[14] Wazwaz A M,Gorguis A.Exact Solutions for Heat-Like and Wave-Like Equations with Variable Coefficients [J].Applied Mathematics and Computation,2004,149(1): 15-29.