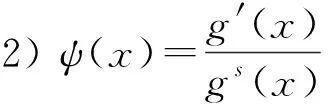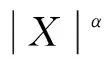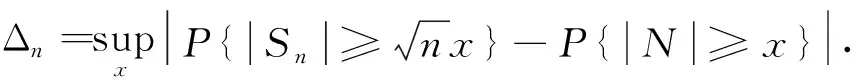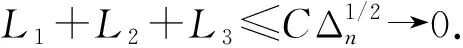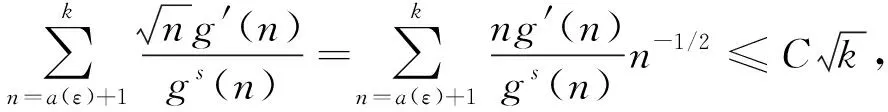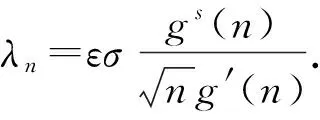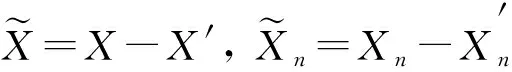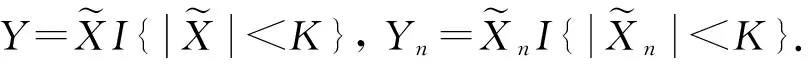独立情形下一阶矩收敛的精确渐近性的注记

孙晓祥,杨丽娟

(吉林农业科技学院 文理学院,吉林 吉林 132101)

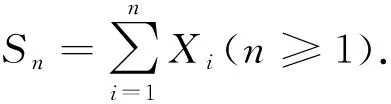
目前,关于随机变量列重对数律、完全收敛及矩重对数律的精确渐近性质已有许多研究结果[1-8].文献[9]给出了关于独立和NA列部分和精确渐近性的一般形式,揭示了拟权函数、边界函数、收敛速度和极限状态间的密切联系.

本文若无特别说明,均以C表示不同的正常数,N表示标准正态随机变量.

定理1[10]对于任意的d>0和β>0,

成立的充要条件是

EX=0,EX2=σ2.

(1)

本文对于普通的拟权函数和边界函数,将上述结果推广到如下更一般的形式.

定理2设0

1)g(x)↑∞,x→∞;

则

(2)

成立的充要条件是式(1)成立.

注1由于在上述级数中增加或减少有限项不改变结果,故为简便,以下一律从n=1开始记,并假设g(x)和g′(x)(或ψ(x)等)在[1,∞)上有定义并单调,不影响g(x)的普遍性.

注2满足定理2条件的g(x)有很多种,如xα,logβx,loglogγx,α>0,β>0,γ>0等,但指数函数不在此列.

注3在定理2中,令g(x)=(loglogx)(2β+d)/2,s=d/(2β+d)(其中:β>0;d>0),即可得到文献[10]的定理1,从而推广了已有的结果.

令a(ε)=g-1(Mε-1/s),M为任意正实数,g-1(x)为g(x)的反函数.

要证明式(1)⟹式(2),此时不妨假设σ=1.

命题1在定理2的条件下,有

证明: 由注1知,可以在[0,1)中对g(x)作适当的补充定义,使g′(x)保持单调性.做变量代换t=εgs(y),得

由定理2中条件1)和2),有

事实上,当ψ(x)单调非增时,式(3)显然成立;当ψ(x)单调非降时,由定理2中条件2)知,对∀δ>0,存在正整数κ,使得当x>κ时,总有ψ(x)≤(1+δ)ψ(x-1),从而

令δ↓0,即得式(3)中右边不等式.同理可得式(3)左边不等式.命题1证毕.

命题2在定理2的条件下,有

(4)

由Δn的定义及Markov不等式知

证明: 注意到定理2中条件2),类似命题1,可得

命题4在定理2的条件下,有

(5)

证明: 由引理1,可得

其中T>1/(2s).

首先考虑K2,注意到01/s>1,

其次考虑K1,为方便不妨假设T=1,

证毕.

下面证明定理2.由命题1～命题4及三角不等式可证得式(1)⟹式(2).下面证明式(2)⟹式(1).

首先证明EX=0.由式(2),对于任意的ε>0,有

因此EY2≤4σ2.从而令K→∞,有EX2<∞.

最后,同理可证

与式(2)相比较,可得EX2=σ2.

[1] WANG Yue-bao.On Asymptotic for Class of Small Parameters Sequences of B-Valued Dependent Random Variables [J].Acta Math Appl Sinica,1995,18: 344-352.(王岳宝.关于B-值强平稳相依随机变量列一类小参数级数的渐近性 [J].应用数学学报,1995,18: 344-352.)

[2] Davis J A.Convergence Rates for the Law of the Iterated Logarithm [J].Ann Math Statist,1968,39(5): 1479-1485.

[3] Spătaru A.Precise Asymptotics in Spitzers Law of Large Numbers [J].J Theoret Probab,1999,12(3): 811-819.

[4] Gut A,Spătaru A.Precise Asymptotics in the Baum-Katz and Davis Law of Large Numbers [J].J Math Anal Appl,2000,248(1): 233-246.

[5] LIU Wei-dong,LIN Zheng-yan.Precise Asymptotics for a New Kind of Complete Moment Convergence [J].Statist Probab Lett,2006,76(16): 1787-1799.

[6] JIANG Ye,ZHANG Li-xin,PANG Tian-xiao.Precise Rates in the Law of the Logarithm for the Moment Convergence of i.i.d.Random Variables [J].J Math Anal Appl,2007,327(1): 695-714.

[7] ZHANG Yong,YANG Xiao-yun,DONG Zhi-shan.Precise Asymptotics of Law of Iterated Logarithm for Linear Process Generated by Strong Mixing Sequences [J].Journal of Jilin University: Science Edition,2007,45(3): 325-330.(张勇,杨晓云,董志山.由强混合序列生成的线性过程重对数律的精确渐近性质 [J].吉林大学学报: 理学版,2007,45(3): 325-330.)

[8] LIU Jun,DONG Zhi-shan,ZHANG Yong.A General Result on Precise Asymptotics for the Linear Process Generated by Strong Mixing Sequences [J].Journal of Jilin University: Science Edition,2008,46(4): 595-600.(刘君,董志山,张勇.由强混合序列生成线性过程精确渐近性的一般形式 [J].吉林大学学报: 理学版,2008,46(4): 595-600.)

[9] CHENG Feng-yang,WANG Yue-bao.Precise Asymptotics of Partial Sums for IID and NA Sequences [J].Acta Math Sinica,2004,47(5): 965-972.(成凤旸,王岳宝.独立与NA列部分和的精致渐近性 [J].数学学报,2004,47(5): 965-972.)

[10] XIAO Xiao-yong,YIN Hong-wei.Precise Asymptotics in the Law of Iterated Logarithm for the First Moment Convergence of i.i.d.Random Variables [J].Stat Probab Lett,2012,82(8): 1590-1596.

[11] Vladimir R.Proability Theory [M].Singapore: World Scientific,1997.

[12] Hall P,Heyde C C.Martingale Limit Theory and Its Application [M].New York: Academic Press,1980.

[13] Baum L E,Katz M.Convergence Rates in the Law of Large Numbers [J].Trans Amer Math Soc,1965,120(1): 108-123.