不同支承体系曲线梁桥的受力性能研究

李广慧，袁 波

(1.郑州航空工业管理学院土建学院，河南郑州450015;2.中国建筑东北设计研究院有限公司，辽宁沈阳110003)

0 引言

随着交通建设的快速发展，在城市立交桥、城市高架桥以及高速公路匝道等曲线梁桥的建设中，尤其是对于宽度9 m及以下的匝道桥，多采用3～5跨一联的独柱墩连续箱梁结构.但是，这种结构形式的桥梁在使用或施工过程中近年来已发生多起倾覆、支座脱空或超载引起的倒塌事故.较为严重的包括2009年7月津晋高速公路外连续独柱墩C匝道桥因3辆严重超载车辆密集停置在匝道桥外侧，导致桥梁发生倾覆事故;2011年2月21日，浙江省上虞市春晖立交D匝道桥发生突然坍塌［1］.正是由于独柱墩曲线梁桥出现的工程病害，使得部分专家和学者开始质疑独柱墩曲线梁桥的设计合理性和安全性.

关于曲线连续梁桥的研究，国内已有不少报道［2-7］，但现有的研究不能全面揭示曲线连续箱梁桥的受力性能.鉴于此，笔者针对一出现病害的实际曲线连续箱梁桥，分别设计了全抗扭跨支承和两端抗扭、中间跨独柱墩支承两种方案，对比分析了各自的受力特点，对独柱墩支承形式还设计了支座偏心，以探讨独柱墩曲线梁桥的受力性能.

1 计算方案设计

1.1 支承体系设计

曲线箱梁桥的计算方案取自某一发生工程病害的实际曲线箱梁桥，为一互通立交的匝道桥，匝道桥的曲线半径为35 m，跨径布置为四跨一联:23 m+27 m+28 m+22 m，上部结构采用预应力混凝土连续箱梁，全跨等高布置，横截面尺寸如图1所示.下部基础均为钻孔灌注桩基础.

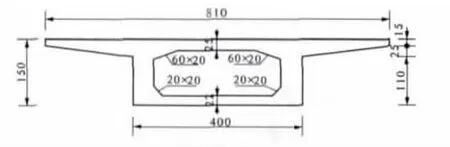
图1 算例匝道桥横截面尺寸Fig.1 Cross section of exam ple ramp bridge

1.1.1 方案一:全抗扭支承体系

如图2所示，是全抗扭支承体系的布设方式，即每个墩的下部结构均采用双立柱，并布设两个支座以达到抗扭的目的.此模型中的所有支座到梁底中心的距离均为141 cm.

图2 方案一:全抗扭支承体系布设图Fig.2 Support system with all torsion-resisting support of schem e 1

1.1.2 方案二:仅两端抗扭支承体系

如图3所示，是仅两端采用抗扭支座的支承体系，即两端的联接墩均为双柱式墩，盖梁上设抗扭支座，中间墩为独柱式墩，采用单向滑动支座或固定支座，根据抗扭跨径的定义——两抗扭支座的间距，本方案抗扭跨径为100 m.此方案中，中间墩的支座布设在梁底中心线上，联接墩上的抗扭支座到梁底中心线的距离均为141 cm.

图3 方案二:仅两端抗扭支承体系布设图Fig.3 Support system with torsion-resisting support only at ends of scheme 2

1.2 加载方案

根据设计规范的要求，考虑的荷载工况共7个，分别是:①恒载，包括梁自重、桥面铺装以及栏杆自重;②预应力荷载;③外侧车道布载(据规范);④内侧车道布载(据规范);⑤整体升温30℃;⑥顶板升温10℃;⑦内外侧腹板温差10℃.

1.3 计算参数

混凝土容重:2 500 km/m3，钢材容重:7 800 km/m3，混凝土强度等级为 C50，弹性模量 E=3.45×1010N/m2，泊松比取0.2，线膨胀系数:1.0×10-5，钢绞线弹性模量 E=1.95 ×1011N/m2，泊松比取0.3，线膨胀系数:1.2×10-5，预应力钢束的预应力损失按30%考虑.

1.4 建议的预应力计算方法

传统的用有限元计算梁的预应力效应的方法有两种:等代荷载法和实体力筋法［8］.在结合上述两种方法的基础上，笔者提出了一种新的计算预应力的方法，称之为“刚臂力筋法”.该方法的原理是:首先在Ansys模型中建立主梁单元和预应力束单元，然后再用刚臂将预应力束单元的节点与和其最近的主梁单元节点连接起来，刚臂单元起到同时传递力和弯矩的作用.算例分析表明，该方法的计算结果与实体力筋法相比，具有较好的计算精度、效率更高，可以满足结构分析需要［8］.

2 计算结果分析

2.1 自重下偏心的计算

为计算自重作用的偏心距大小，取单位弧度的一段曲线梁，如图4建立坐标系，y轴通过截面的几何中心，重力偏心距可由公式(1)至(3)计算:

式中:XP是恒载作用偏心距;d v是微体积元;x是微体积元的x坐标;V是总体积;d A是微面积元;t(x)是微面积元的长度.

图4 恒载偏心距的计算图示Fig.4 Illustration for eccentricity of self-weight

计算表明，在截面尺寸确定的情况下，其自重偏心值与半径成反比关系.对于曲线半径为35 m的曲线梁桥，对图1所示截面得到的自重偏心结果为:铺装层的自重偏心为15.6 cm，栏杆的自重偏心为46.9 cm，梁体的自重偏心为11.4 cm.可见，在用梁单元计算半径较小的曲线梁时，自重偏心的影响不可忽略，计算时应对梁单元施加相应的扭矩［8］.

2.2 两种支承体系曲线梁桥受力特性对比分析

针对方案一和方案二的曲线连续箱梁桥进行了7种荷载工况作用下的静力分析，其内力范围分别示于表1和表2中.

表1 方案一曲线梁桥的内力范围表Tab.1 The range of internal forces of curved bridge under scheme 1

表2 方案二曲线梁桥的内力范围表Tab.2 The range of internal forces of curved bridge under scheme 2

2.2.1 竖弯弯矩

从表1和表2中的数据，可以看出:

(1)在恒载和预应力作用下，两个方案竖弯弯矩的最大、最小值和分布情况变化幅度不大，说明在这两种工况下曲线梁桥竖弯弯矩对支承体系的改变不敏感.而且，在自重作用和车道荷载作用下的竖弯弯矩图的分布形式相似，均在支座处出现最大负竖弯弯矩跨中出现最大正竖弯弯矩，如图5(a)所示，预应力作用下的竖弯弯矩图与之相反，如图5(b)所示.

(2)外侧车道荷载比内侧车道荷载所产生的弯矩要大，一方面是由于外侧车道的弧长比内侧车道弧长大，另一方面则是外侧车道对梁的偏心使得梁还受到向外翻转的扭矩，这个扭矩又会增加梁的弯矩.另外，外侧车道荷载在中间跨上几乎只产生竖弯正弯矩，而内侧车道荷载在中间跨上几乎只产生竖弯负弯矩.这种差别随着曲线桥半径的减小而增大，对于直线桥则不存在此差别.

(3)在顶板升温10℃作用下，两种支承体系的竖弯弯矩图分布情况变化不大，产生的弯矩值约为梁体自重所产生弯矩的54%.如图5(c)所示.而方案二的弯矩最大值减小了约30%.说明方案二比方案一抵抗顶板升温产生竖弯弯矩的能力强.

2.2.2 平弯弯矩

从表1和表2中可以看出，无论是方案一还是方案二，产生平弯弯矩的主要因素均是预应力、整体升温和环内外温差.并且两种方案下由这三种荷载产生的弯矩最大、最小值与分布情况非常接近，说明曲线梁桥的平弯弯矩对支座体系的改变不敏感.因此，在曲线梁桥的设计中，将部分预应力束布设在两侧的腹板内是一种较为合理的方法，预应力束不但能够起到抵抗竖向弯矩的作用，还有很好地抵抗平弯弯矩的作用.

2.2.3 扭矩

为了便于比较，对7种荷载工况进行组合，一共得到48个可能的效应组合工况，绘制出方案一和方案二曲线梁桥的扭矩包络图，如图6和图7所示，而图8则是方案二设置支座偏心以后的扭矩包络图.

结合表1、表2和图6至图8，可以得出:①曲线梁桥的扭矩主要由恒载、预应力以及顶板升温作用产生.其中，预应力产生扭矩是由于其所生的径向力未通过箱梁截面的扭转中心所造成的.②相比方案一，方案二在两端抗扭支座处的扭矩最大，在不设置支座偏心情况下约为方案一的2.4倍.③在设置偏心后，方案二扭矩包络图绝对值仅是方案一的1.3倍左右.说明设置支座偏心以后，即便仅在两端设置抗扭支座，也可在很大程度上减小曲线梁桥扭矩，效果明显.

2.2.4 竖向剪力

从表1和表2中的结果可以看出，在各种荷载工况下，两种支承体系的曲线梁桥所产生的竖向剪力最大、最小值及其分布情况非常接近，说明曲线梁桥的竖向剪力对支座体系的改变不敏感，而且与直线桥的剪力情况大致相当.

2.2.5 支座反力

方案一曲线梁桥在各种工况下的竖向和水平支座反力如表3所示.方案二曲线梁桥根据2.1节自重偏心计算结果，将支座处的支承合力点(单支座时则为支承点)沿径向向外偏移，得到各种工况下竖向和水平支座反力结果，如表4所示.

从表3和表4结果可以看出:①引起内侧支座出现负反力的主要因素是恒荷载、顶板升温作用和外侧车道荷载，这一点也可由扭矩图得到解释，而一般的板式和盆式橡胶支座在受拉时容易破坏，从而导致支座脱空;对方案一来说，最容易出现负反力的支座是中间墩的内侧支座;对方案二来说，最容易出现负反力的支座是联接墩上的内侧支座.②针对方案二，支座偏心的设置可以有效地减小抗扭支座内侧支座的负反力，其最大负反力比不设支座偏心时大约减小66%左右.

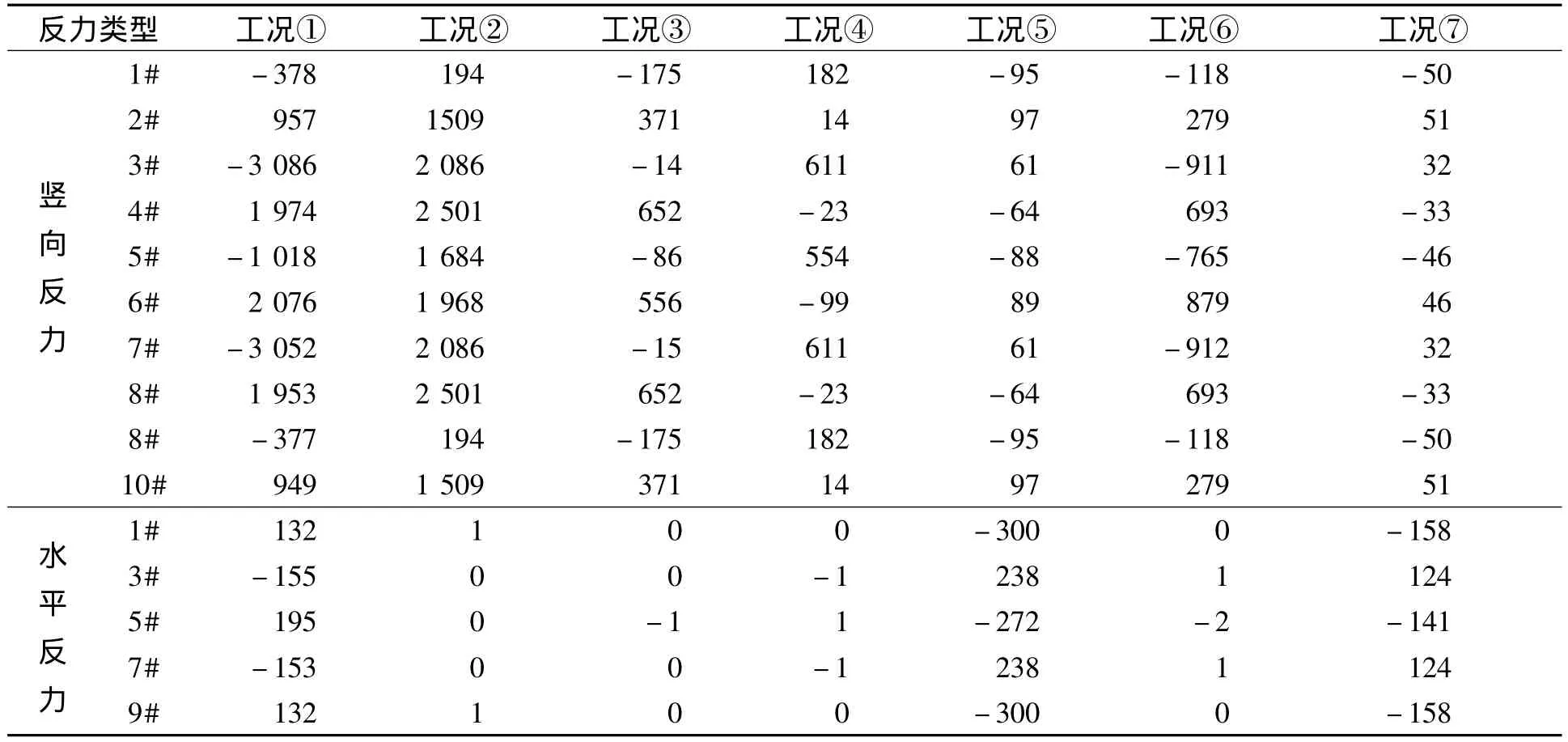
表3 方案一曲线梁桥的竖向和水平支座反力Tab.3 The reaction forces of support at both vertical and horizontal directions of Scheme 1 kN

3 结论

通过对2种支承体系下曲线梁桥在7种荷载工况下的静力分析，得到一些有用的结论.

(1)在用梁单元计算曲率半径较小的曲线梁桥时，梁体自重偏心的影响是不可忽略的，内力计算时应该对梁单元施加相应的扭矩.

(2)曲线梁桥在竖向荷载(自重与车道荷载)、预应力荷载以及顶板升温作用下会产非常大的扭矩，并且在这些扭矩作用下梁体都有向环外翻转的趋势，且以上3种荷载工况下，方案二的扭矩都比方案一要大.

(3)针对方案二的曲线梁桥，抗扭支座的内侧支座容易出现竖向负反力，即发生“脱空”现象.设置支座偏心可以有效地改善曲线梁桥的扭矩分布和减小竖向负反力的大小.并且，随着抗扭跨径的增加，支座偏心对扭矩改善的幅度越大.

(4)曲线梁桥的单向滑动支座和固定支座都容易出现较大的水平剪力，因此应在进行曲线梁桥设计时予以高度重视，以防支座被剪坏.

因此，只要根据计算设置适当的支座偏心，仅在两端设置抗扭支座、中间跨采用独柱墩(即方案二)设计方案的受力性能是良好的，在实际运营中，采取必要的管理措施，如设置限载和曲线梁桥外侧禁停标志、安装技术设施，严控超载车辆在桥上滞留和偏心等，就可以确保独柱墩曲线梁桥的安全，不必因为出现一些工程病害否定这种桥型的合理性.

表4 方案二曲线梁桥设置支座偏心后竖向和水平支座反力Tab.4 Reaction forces of support at both vertical and horizontal directions of Schem e 2 with eccentricity kN

［1］ 冯苠，李会驰，赵君黎.公路桥梁独柱墩结构安全风险综述［J］.公路交通科技:应用技术版，2011(12):17-21.

［2］ 宫平，青金彪.深圳某立交N4匝道桥梁体转动分析和加固分析［J］.特种结构，2001，18(4):67-68.

［3］ 杨党旗.华强立交A匝道独柱曲线梁桥病害分析及加固［J］.桥梁建设，2003，(2):58-61.

［4］ 王吉英，屈国，郝海洪，等.曲线匝道桥支座脱空原因分析及加因处理［J］.北方交通，2006(4):56-58.

［5］ 李广慧，余正武，王用中.曲线连续梁桥的病害与温度效应［J］.公路交通科技，2008，25(1):58-63.

［6］ 李广慧，袁波.曲线箱梁桥的支座偏心优化设计［J］.公路，2012(9):66-69.

［7］ 王旭阳.绵竹市回澜匝道桥抗震分析［D］.成都:西南交通大学交通学院，2010:1-9.

［8］ 袁波.曲线梁桥的受力性能分析与支承优化设计［D］.郑州:郑州大学土木工程学院，2011:24-27.