交错多通道采样信号的分析与重构方法
李玉玲,翟盼盼
(河南大学计算机与信息工程学院,河南开封475004)
0 引言
近年来,对高带宽信号或者大采样率信号的处理通常需要使用时间交错数模转换器[1].如果采样信号的带宽很大,直接对模拟信号采样会非常困难,因此,通常利用多个通道来对高带宽信号进行并行采样.由于通道之间存在时间延迟,导致实际的采样为均匀采样或非均匀采样[2-3].在单通道或多通道A/D转换器采样系统中,对采样信号的重构必须考虑量化影响[4].当前,人们常采用过采样的方法减轻量化影响[5].
针对上述问题,笔者拟基于交错环境中的多通道测量值、量化影响以及过采样的条件,设计一个最优重构滤波器.首先,对量化误差使用加性噪声进行建模,针对多通道采样,当通道之间的量化步长不相等且通道之间的相对时间也不满足均匀采样时,通过增加SQNR对信号进行最优重构.其次,在通道之间的相对时间不匹配的情况下,对量化步长进行合理的调整,来达到对信号进行最优重构.最后,对通道之间的量化步长以及相对时间进行调整,以得到最优补偿滤波器.有限信号x(t)的Nyquist采样率为1/TN,每个通道的采样率1/T=1/LTN,过采率为ρ=M/L>1.现将图 1定义为理想模型,即 xm[n]=x(nT-τm),通道M的时间延迟为τm.

图1 多通道采样图Fig.1 Multi-channel sampling
多通道采样系统的交错输出采样值如图2所示.通过对时间延迟τm的选择,可使得采样为均匀采样或周期性非均匀采样[6].这里特别指出,交错序列xM/L[n]是在 M/L倍 Nyquist采样率下对x(t)进行均匀采样得到的输出值,xM/L[n]是x(t)的周期性非均匀采样值.
1 多通道采样和重构
本节对多通道采样系统进行描述,针对均匀采样和周期性非均匀采样设计完美重构滤波器.
1.1 过采样多通道系统
考虑多通道采样系统如图1所示.其中,带宽

图2 交错输出采样值Fig.2 Interleaving the output samp les
1.2 完美重构
当不存在量化误差或多通道系统的采样率不小于输入信号的Nyquist采样率时,采样信号x(t)利用多通道输出值x~m[n]=xm[n]可得到完美重构.例如,完美重构可通过如图3的滤波器处理来得到,其将序列x~m[n]集合到一个扩展器组合中,对采样信号x(t)在Nyquist采样率下得到的统一样本进行sinc插值来重构原始信号.
当如图1的多通道系统中的时间延迟满足式(1)时,从图3中选择重构滤波器为式(2).
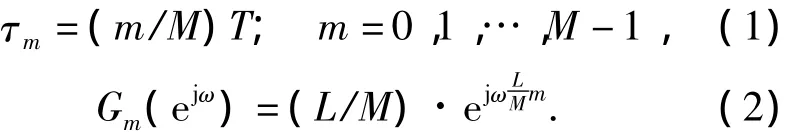
此滤波器可对采样信号x(t)进行完美重构.通过选择滤波器Gm(ejω),对通道之间的时间延迟τm的空间非均匀性进行补偿,以得到x(t)的均匀采样值 x~[n].

图3 多通道系统重构图Fig.3 Multichannel reconstruction
对于x(t)的完美重构可以通过如图3的系统得到,前提是:
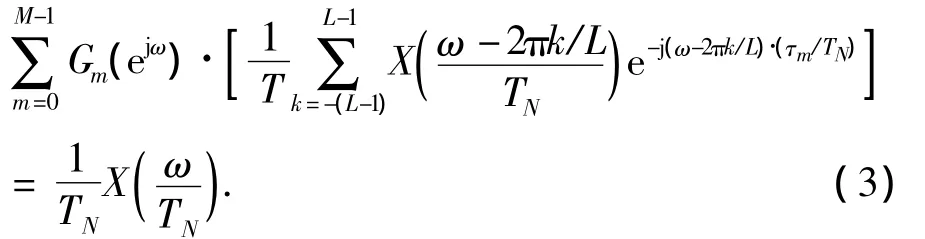
由于每个通道的采样率是输入信号Nyquist采样率的1/L倍,对式(3)进行化简,得到式(2)的约束条件如式(4)所示:
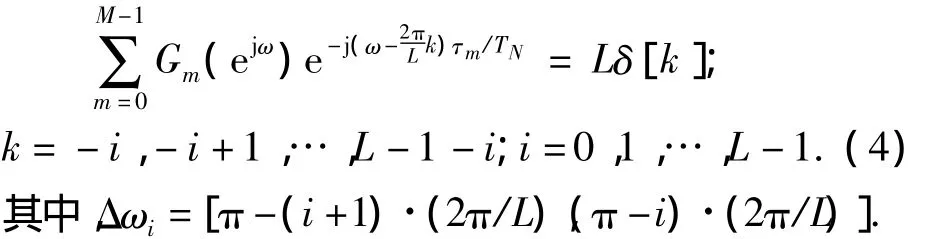
当M=L时,式(4)可以唯一地确定重构滤波器Gm(ejω).当M>L时,满足过采样,用剩余的M-L个自由度来设计重构滤波器.这些情况均会在第2节中得到充分的讨论.
2 存在量化误差下多通道采样和重构
2.1 量化噪声
针对量化后产生的量化误差使用加性噪声模型,多通道采样系统的输出采样值表示为
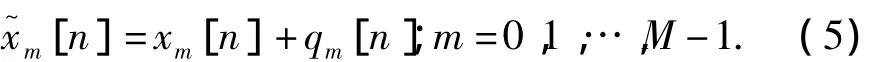
假设qm[n]是一个白噪声随机过程,均匀分布在[-Δm/2,Δm/2]内;Δm是通道 M 的量化步长;qm[n]的方差为互不相关的,qm[n]和采样值x(t)也不相关.
Nm代表通道M中分配的位数,其与量化步长的关系是Δm=2X/2Nm,X代表数模转换器的满刻度.
将多通道输出值 x~(t)的总噪声表示为e(t),e(t)是一个广义平稳随机过程,即
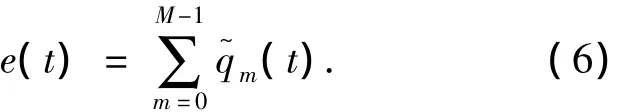
由于通道之间的量化噪声是不相关的,则e(t)的总平均功率值是E(e2(t)),表示为
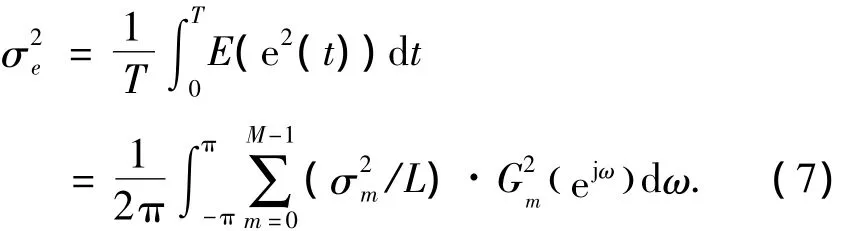
2.2 最优重构滤波器
设计重构滤波器Gm(ejω)的方法有多种,其中一种就是通过利用所有的自由度来最小化噪声重构误差以得到信号的重构[7].本小节假设已知信号的带宽,在满足式(4)的约束时,通过最小化来设计最优重构滤波器Gm(ejω).引用文献[7]中相关公式,得到:
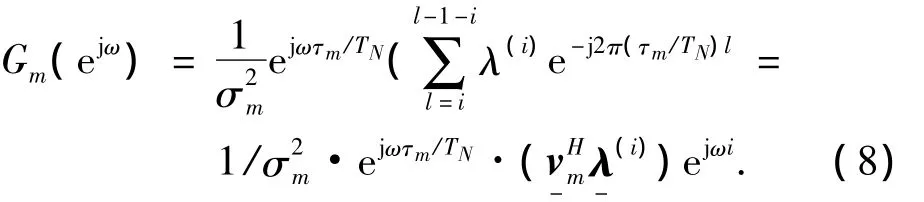
其中,用 Λ(i)(ejωm)代表有限长度序列{λ(i)k}L-1-ik=-i的离散时间Fourier转换,即
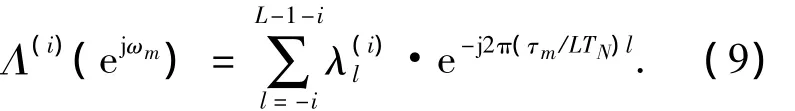
此时,其频率大小为

由于AM是一个共轭矩阵,即
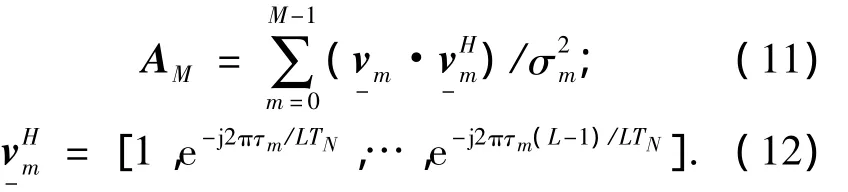
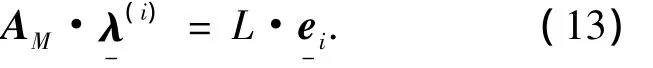
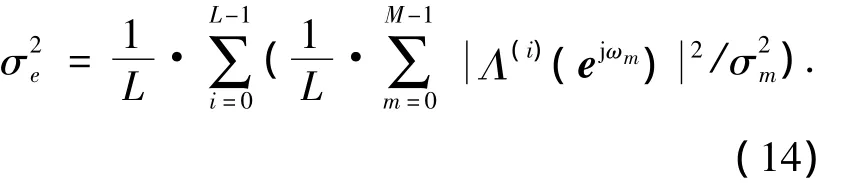
另外,在将式(8)带入式(7)的同时,也得到:
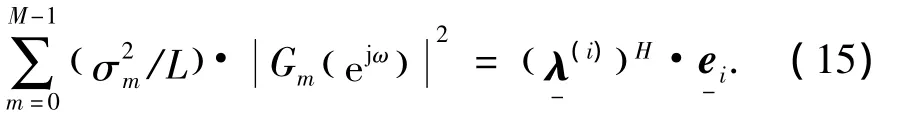
注意,由于AM在上式中大于零,将转换为
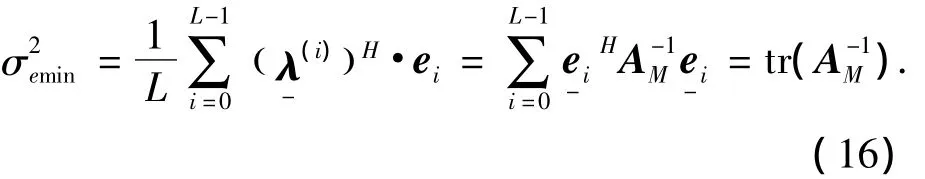
当M=L时,得到式(8)中的最优的滤波器和通过满足约束式(4)得到的唯一解是一致的.根据文献[7]中第二章第二节的证明,则可得到:
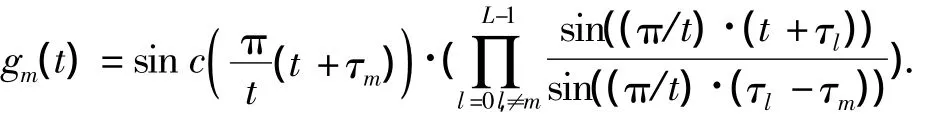
因此,在不存在量化误差的情况下,按照上式计算,将图3中的输出值x~(t)表示为
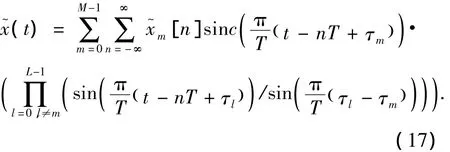
式(17)是对连续时间信号x(t)的完美重构.按照文献[7]中的方法,输出噪声平均功率为
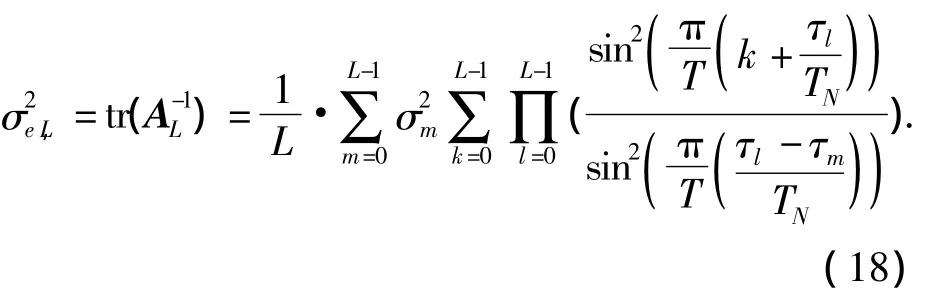
M >L时,利用Woodbury矩阵对式(16)进行简单递推,将输出平均噪声功率更新为

2.3 多通道采样系统中的最优SQNR
以上分析了如图1的多通道系统的中量化对重构带来的影响,同时也设计出了最优重构滤波器.在多通道采样重构系统中,有效的SQNR可以对采样信号进行完美重构,但SQNR主要依赖于通道之间的量化步长、相对时间和过采样率.接下来讨论如何对这些参数进行优化,以得到一个最优的SQNR.分析式(13),得
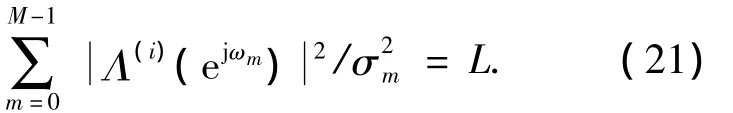
针对式(21)使用Cauchy-Schwartz不等式,可得
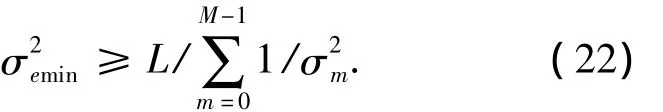
如果要使式(22)中的等号成立,当且仅当:
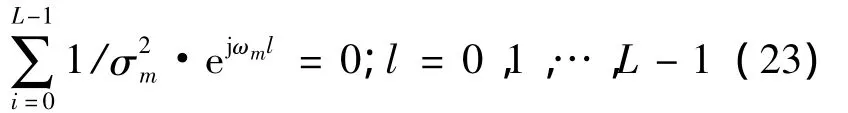
当如图1的多通道系统中量化器使用的相同的量化步长,式(1)的τm可对采样信号进行最优重构,接下来会对此证明.此时,式(8)的最优重构滤波器退化为式(2)中的非整数时间延迟,即
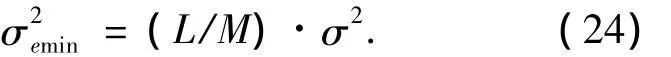
这里σ2表示所有通道的量化噪声方差的平均值.假设每个通道的量化噪声的方差相等,则
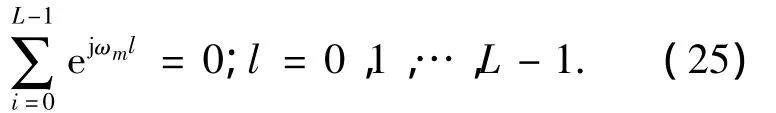
当重构系统中通道之间的量化步长相同,平均量化噪声功率为(L/M)·σ2,此时为均匀采样,可对采样信号达到最优重构.关于时间延迟τm的其它选择,因不满足式(24)中的约束,易产生较差SQNR.
因为通道之间的量化步长不同[8],所以通道的量化噪声qm[n]的方差σm2也不相同,接下来讨论如何对方差σm2进行选择才能获得较好的SQNR.为了便于比较,这里假设所有通道之间的总量化噪声功率的平均值固定为σ2:

利用Cauchy-Schwartz不等式,式(26)转换为
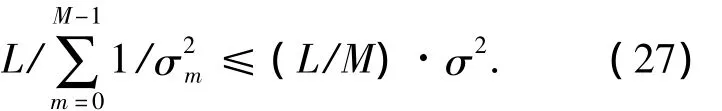
如果式(27)成立,当且仅当满足条件:
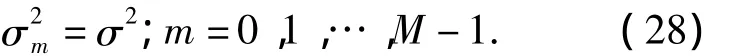
通过上述分析采取如下措施:对量化器使用加性噪声建模,并对通道间的量化器进行不同精度的选择,以降低平均量化噪声功率;通过设计量化器以消除时间不匹配性带来的量化影响;通过调整通道之间的量化步长得到均匀采样,以便得到一个较好的SQNR对信号进行最优重构.
3 仿真分析
在本节中,考虑如图1的多通道采样系统,其中,M=3;L=2.通过以上分析,首先可得
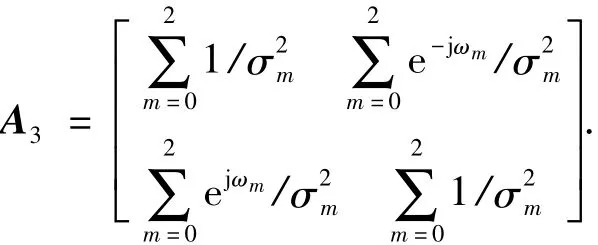
假设 τ0=0(ω0=0),可得
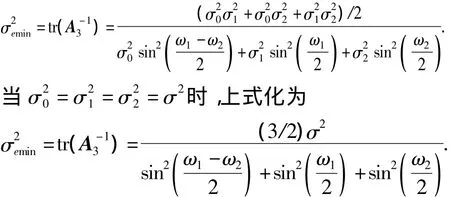
第一种情况,将通道之间的量化补偿固定为一个常量,在最优重构的约束下对时间延迟τm进行选择.图4显示比较因子,表示为在多通道采样和重构系统中输出噪声平均功率与最小噪声功率的比值,其前提条件为最大的比较因子γ在τ1=-τ2= ±(2/3)·TN时得到,此时最小的平均噪声功率为.在重构系统中,令通道之间的量化步长相同,得到最小的平均噪声功率为(L/M)·σ2,此时达到最优重构.即通道之间的量化步长相同,如果要得到最优的重构滤波器,必须得到最小的平均噪声功率,此平均噪声功率为(L/M)·σ2.
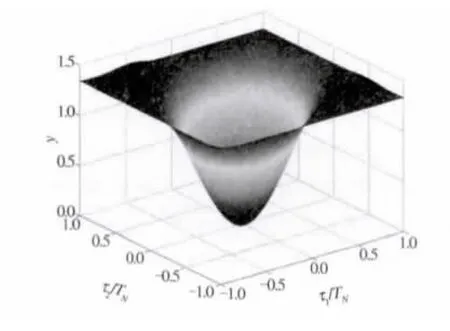
图4 均方误差比较Fig.4 The com pare of reduction factor
第二种情况,通过适当设计通道之间的量化步长来对时间延迟的空间不匹配性进行调整,以达到信号的最优重构.假设这3个通道分配相同的量化步长,每个通道都分配4位,当τ0=0,τ1=TN/8,τ2=-(3/4)·TN时,输出噪声功率与在均匀采样时相比增长了20%.但是,当每个通道之间的量化步长不同时,相对于均匀采样,重构误差的方差可得到一个更小的值.表1通过对通道之间分配不同位数的最小方差与分配位数固定的最小方差进行比较,分析通道之间分配的位数的不同对最小方差的影响.令通道之间分配固定位数为4位,其余均是总分配位数不变,但各个通道之间的相对分配的位数发生变化,变化范围为增大或减少一位,于此对最小方差进行比较.从表1中得到当通道之间的量化步长不同,均匀采样已不能对信号进行最优重构.所以,当通道之间量化步长不同时,相应的均匀采样已经不能对信号进行最优重构,对通道之间分配的位数进行相应的调整,以便对信号进行最优重构.

表1 分配不同位数的方差比较Tab.1 The performance gain for different bit allocations
第三种情况,利用均匀采样下的量化噪声的方差与其他情况相比较,其中通道之间的时间延迟范围为[-TN,TN],得到图5中的仿真结果.结果表明,此种情况下的仿真结果相比于均匀采样,提高了12.5%,满足最优重构的时间延迟为τ1=-τ2= ±0.54TN.

图5 相对性能比较Fig.5 The com pare of relative performance
由上述得到,由于多通道采样重构系统中时间延迟的空间非均匀性,导致交错多通道输出等同于周期性非均匀采样;此时通道间相同的量化步长已经不能满足最优的重构.同时也证明了对通道间的量化器使用不同精度,以便减少噪声方差.另外,当固定通道之间的量化步长且不等,相同的通道间相对时间已不能满足最优重构;此时通过对相对时间进行调整,得到一个更低的噪声方差,对信号进行最优重构.
4 结论
首先考虑交错式多通道环境中量化对信号重构的影响,并证明在多通道采样环境中,当通道之间的量化步长固定并且相同时,对信号进行最优重构的条件是当且仅当采样是均匀采样.其次对存在量化误差的情况,基于将噪声功率最小化的原则,对信号进行最优重构,设计了最优重构滤波器.最后针对通道之间量化步长不同、时间延迟为非均匀采样时,如何对量化步长、时间延迟进行合理的调整以达到对信号的最优重构,并做了相应的仿真验证.
[1] 杨泉玖,杨光,马兵,等.一种高速多通道核辐射信号采集系统的设计[J].郑州大学学报:理学版,2005,24(4):44-46.
[2] 阙大顺,高勇,王艳丽.模数转换器工作原理及应用[J].武汉理工大学学报,2003,25(4):129-132.
[3] 曾浩,潘卉青,叶芃,等.高速非均匀采样信号的重构方法[J].自动化仪表,2010,31(9):12-14.
[4] MARZILIANO P,VETTERLIM.Reconstruction of irregularly sampled discrete-time bandlimited signalwith unknown sampling locations[J].IEEE Trans Signal Process,2000,48(12):3462-3471.
[5] HO C Y,LING B W K.Noise analysis of modulated quantizer based on oversampled signals[J].Proc ICASSP,2006,14(19):728-731.
[6] RABINER L,SCHAFER R.Theory and applications of digital speech processing[M].Englewood Cliffs,NJ:Prentice-Hall,2010.
[7] MAYMON S.Sampling and quantization for optimal reconstruction[D].Boston,Massachusetts:Massachusetts Institute of Technology,2011.
[8] MCMICHAEL JG.Timing offset and quantization error trade-off in interleaved multi-channel measurements[D].Boston,Massachusetts:Massac-husetts Institute of Technology,2011.

