基于Rife算法和相位差法的正弦信号频率估计

(杭州电子科技大学通信工程学院，浙江 杭州310018)

0 引 言

频率估计在雷达、声纳和通信领域均有广泛的应用，而含噪的正弦信号频率估计的方法各有优劣。最大似然估计算法估计方差逼近克拉美罗限，是最优估计，但其计算复杂度大，不利于实时处理[1]。而基于FFT算法的插值算法速度快、实时性好、易于实现，常用的方法有:Rife 法、相位差法等[1-3]。Rife算法在无噪声或信噪比较高、采样点数适宜的情况下，估计精度较高，而对于那些信号频率靠近DFT 量化频率点，且在信噪比低的情况下会导致插值方向错误，增大估计误差。相位差法具有良好的估计性能，而在信号频率接近两个相邻量化频率点的中心时，估计性能不如Rife算法。根据这两种算法的互补特性，本文提出了一种基于Rife算法和改进的相位差法的综合算法。计算机仿真结果表明本文算法准确有效，估计均方根误差接近克拉美罗限，在信噪比较低的情况下也表现稳定，具有一定的工程应用价值。

1 Rife算法

单一频率复正弦信号s(t)=Aej(2f0t+Φ0)，其中A，Φ0分别为振幅和初相，f0为频率;在0 ～T时间内对信号进行采样，采样点数为N，采样频率为fs，得到采样序列s(n)=Aej(2 nf0/fs+Φ0)，对采样序列进行N点DFT 变换得到S(k)。

设k0为最大谱线位置，即Rife算法估计频率f0的近似表达式为[2]:其中，当时，r=1，当时，r=-1。

2 相位差法

对原始单一频率复信号s(t)=Aej(2f0t+Φ0)采两段连续样本，每段采样点数为M=N/2，则有:

两段信号相位分别为Φ0，Φ1，令f0=(k1+α)fs/M，其中k1为s1(n)的最大幅值谱线位置，得α =(Φ1-Φ0)/2，分别对序列s1(n)，s2(n)做M点DFT 变换，求出各自幅值最大值谱线对应相位Φk1Φk2，那么根据文献3可以计算得到=(Φk2-Φk1)/2 =ΔΦ/2，其中ΔΦ 要调整到(-，)，那么估计频率

3 综合算法

传统的相位差法要对两段序列分别做FFT，计算量较大，本文给出一种改进的相位差算法以减少它的计算量。算法具体实现过程如下:对于样本长度为N的序列s(n)，利用Rife算法可以得到最大谱线的位置k0，而s1(n)相当于对序列s(n)加了长度为M的窗(M ＜N)，也就是样本长度为M，由于信号s(n)与s1(n)的频率是相同的，得到s1(n)，s2(n)对应的幅频最大值谱线位置为k1=k2=Mk0/N，那么计算序列s1(n)，s2(n)幅频最大值谱线对应的相位，只需要计算这两个值，利用便可得到相应的相位值，从而减少了计算量，提高了运算速度，因为原本相位差法要做两次M点的FFT，现在只需要计算两个单点上的DFT 即可。综合算法的具体实现步骤如下:

(1)对采样序列s(n)做N点DFT 变换，得到幅值最大值谱线位置k0，根据Rife算法计算

(2)做出判断，若0.3≤|δ^|≤0.5，则直接代入f0=(k0+)fs/N 求得估计频率，否则转步骤3;

(3)根据Rife算法求得的结果，利用改进的相位差法，计算频偏=(Φk2-Φk1)/2 =ΔΦ/2，其中ΔΦ 要调整到(-，)，最后求得频率=(k1+)fs/M。

4 计算量分析

Rife算法需要做一次N点的FFT，相位差法需要做两次N/2点FFT，综合算法中要用到相位差法求解时，只要在Rife算法的基础上再计算两个单点的N/2点DFT 即可，这需要增加N次复数乘法和N-2次复数加法，考虑到综合算法中并不是每个频率点的估计都会用到相位差法，根据所设置的门限值可知，用Rife算法估计时直接可行的概率为2/5，因此从统计角度，综合算法的计算量为次复数乘法和次复数加法，比M-Rife算法的计算量的计算量小[4]。

5 仿真实验

仿真参数如下:接收信号x(t)=Acos(2 f0t+Φ0)+n(t)，n(t)是均值为0，方差为σ2的高斯白噪声，信噪比记为SNR=A2/2σ2。fs=200kHz，N=1 024，Δf=fs/N，ΔT =1/fs，用DFT 作频率粗估计，其均方根误差[1]为

复正弦信号当其相位未知的情况下，频率估计的克拉美罗限为[5]实正弦信号频率估计方差下限为相同条件下复正弦信号的方差下限的两倍[6]。

设f1为DFT的某个量化频率，现取f1=200fs/N，并从f1到f1+Δf/2 取11个离散的频率点作为待估频率，即f0i=f1+iΔf/20，i=0，1，…，10，对频率为f0i的正弦信号按Rife 法，相位差法及综合算法分别进行1 000次的Mento-Caro仿真。如表1-3所示，i =0，2，4，6，8，10 等6个离散频率点在不同信噪比SNR(分别为6dB，0dB，-3dB)条件下的Rife算法，相位差法和综合算法的频率估计的均方根误差，平均绝对误差，标准方差:

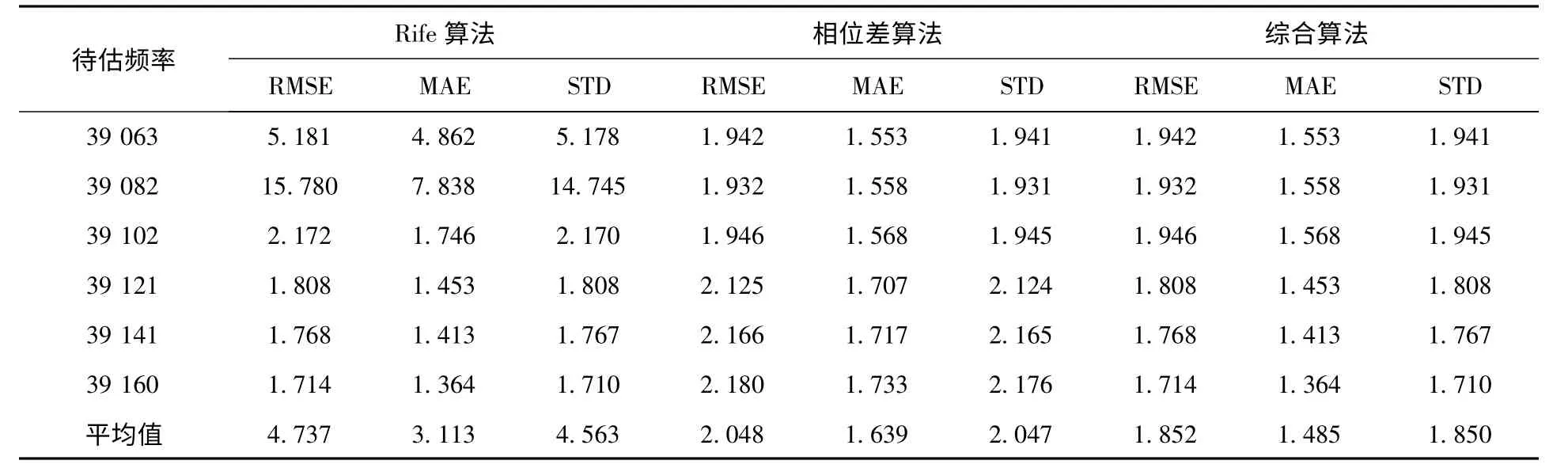
表1 3种频率估计算法在SNR=6dB条件下的仿真结果 (Hz)

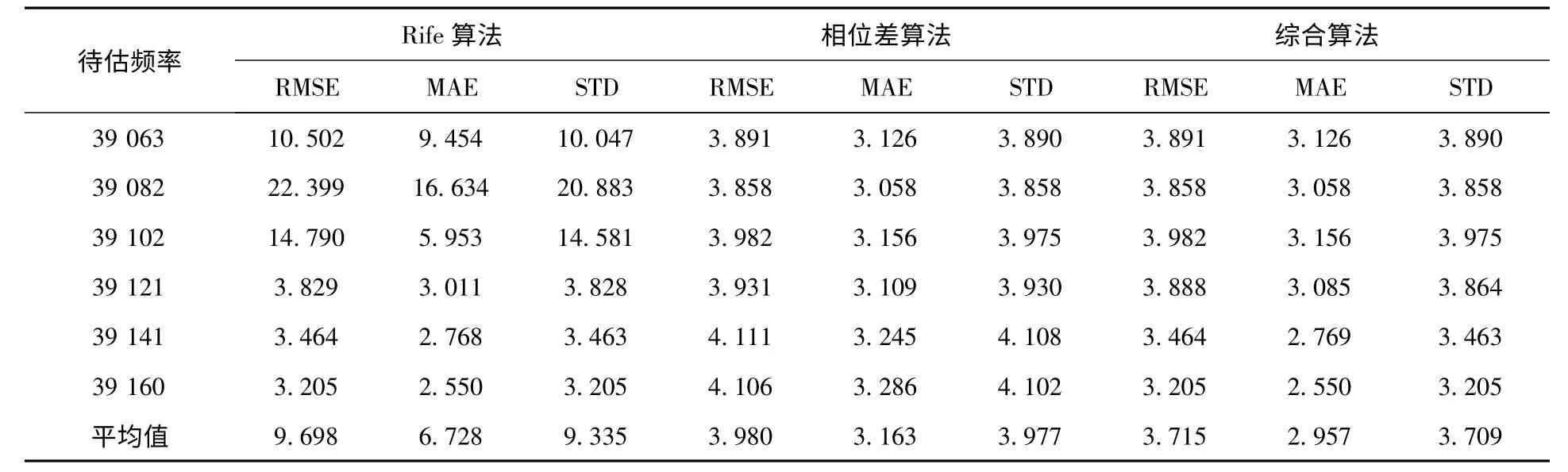
表2 3种频率估计算法在SNR=0dB条件下的仿真结果 (Hz)

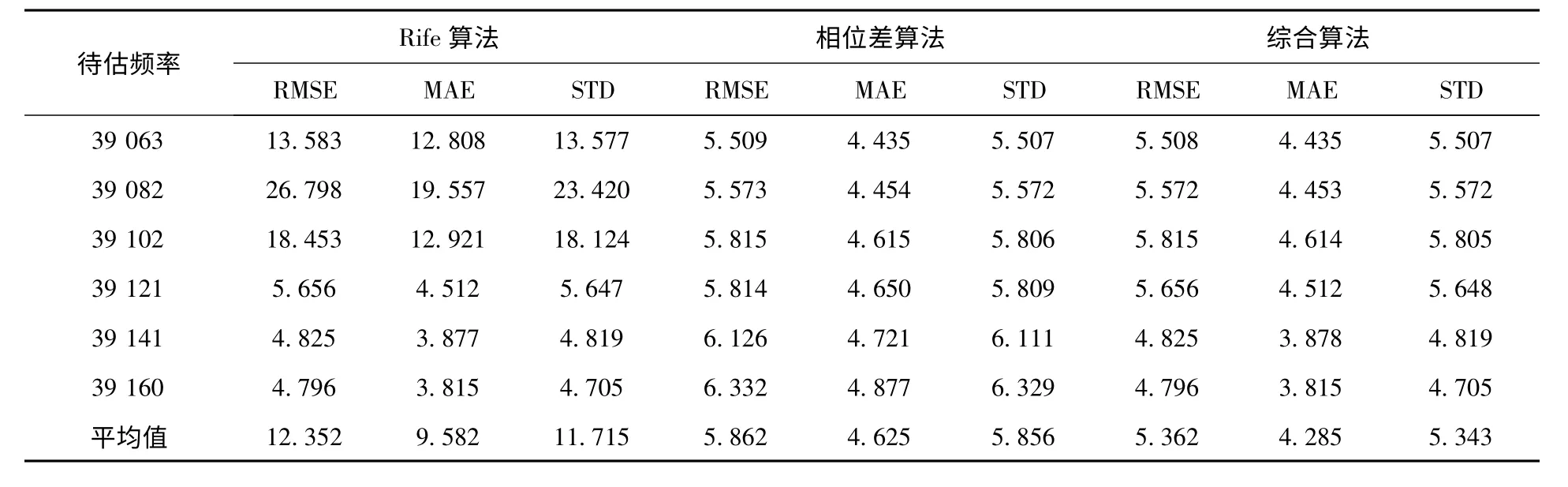
表3 3种频率估计算法在SNR=-3dB条件下的仿真结果 (Hz)

从仿真结果可以看出，综合算法所得到的结果有时与Rife算法相近，有时与相位差算法相近，这是因为这两种算法具有互补性，是通过设立一个门限值，选取其中一个合适的频率估计算法来进行频率估计，因此就会出现上述的结果，综合算法提高的是频率估计的总体性能。也可以得出，Rife算法在待估频率靠近DFT 量化频率点时的误差很大，而相位差法和综合算法的性能较为稳定，且综合算法在信噪比为6dB的情况下平均均方根误差仅为DFT 粗估计的3.3%，在信噪比为-3dB的时候也仅为DFT 粗估计的9.5%，在整个频段上的估计精度也较高。如图1所示不同信噪比条件下的3种频率估计算法的均方根误差平均值与克拉美罗限的比较。从图1中也可以看出综合算法的均方根误差平均值更接近克拉美罗限。所以从通过设立一个门限值，对不同频段采用不同的频率估计算法以提高整体频率估计性能总体性能上而言，综合算法优于Rife算法和相位差法。

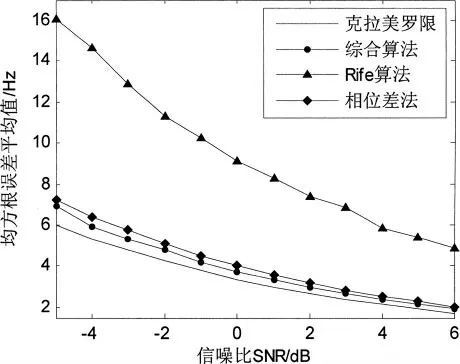
图1 3种算法均方根误差平均值与克拉美罗限比较图

6 结束语

Rife算法和相位差法都是常用的基于FFT 插值算法，它们的性能在不同频段各有优劣，综合算法则是利用两者互补的关系来进一步提高估计精度和稳定性，仿真结果也验证了本算法的准确有效，均方根误差能够很好的接近克拉美罗限，而且综合算法的计算量增加不大，易于实现，实时性好，因此在工程上具有一定的应用价值。

[1]王宏伟，赵国庆.正弦波频率估计的改进Rife算法[J].信号处理，2010，26(10):1 573-1 576.

[2]Rife D C，Vincent G A.Use of the discrete Fourier transform in the measurement of frequencies and levels of tones[J].Bell Syst Tech J，1970，49(2):197-228.

[3]谢明，张晓飞，丁康.频谱分析中用于相位和频率校正的相位差校正法[J].振动工程学报，1999，12(4):454-459.

[4]王宏伟，赵国庆，齐飞林.一种实时精确的正弦波频率估计算法[J].数据采集与处理，2009，24(2):208-211.

[5]Rife D C，Boorstyn R R.Single tone parameter estimation from discrete-time observations[J].IEEE Trans infom Theory，1974，20(5):591-598.

[6]齐国清.几种基于FFT的频率估计方法精度分析[J].振动工程学报，2006，19(1):86-92.